Конспект уроку в 9 класі "Розв'язування вправ і задач на арифметичну та геометричну прогресії"

Тема. Розв’язування вправ і задач на арифметичну та геометричну прогресії.

Мета: узагальнити і систематизувати матеріал про про арифметичну та геометричну прогресії, розкрити значення теоретичних знань для практичної діяльності людини; розвивати логічне мислення, вміння порівнювати, аналізувати; виховувати інтерес до математики.

Тип уроку: урок узагальнення і систематизації знань.

Методи навчання: інтерактивна вправа «Асоціативний кущ», домашні проекти, колективні вправи, вправа «Незакінчене речення».

Обладнання: проектор, презентація задачі «Поливання городу»,  плакат до задачі «Купівля коня», картки з формулами, презентації  з умовами завдань.

Хід уроку

1. Організаційний момент

Запишіть у зошити сьогоднішню дату, класна робота.

2. Повідомлення домашнього завдання

Запишіть у щоденники домашнє завдання: повторити §60-62, виконати № 242, №263.

3. Повідомлення теми та мети уроку

Тема сьогоднішнього уроку: «Розв’язування вправ і задач на арифметичну та геометричну прогресії». Мета уроку: повторити і узагальнити теоретичні знання про арифметичну та геометричну прогресії, повторити основні типи вправ, показати практичне використання прогресій у житті людини, розвивати логічне мислення, виховувати інтерес до математики.

Девізом нашого уроку є народна мудрість: «Збирати знання, як краплі в долоні, бо з крапель утвориться море».

Що ви очікуєте від сьогоднішнього уроку?

4. Мотивація навчальної діяльності учнів

На попередніх уроках ви переконалися, що є багато алгебраїчних і комбінованих задач на прогресії. А де ж використовуються вони в життєвих ситуаціях? Про це ви сьогодні і дізнаєтеся.

5. Відтворення та коригування опорних знань

А зараз повторимо поняття, які пов’язані з прогресіями за допомогою інтерактивної вправи «Асоціативний кущ».

В центрі дошки знаходиться поняття «арифметична прогресія». Що воно означає? Тепер вам потрібно  пригадати і дати означення термінам, які з нею пов’язані. Правильна відповідь оцінюється 2 балами, які ви виставляєте на полях зошитів.

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

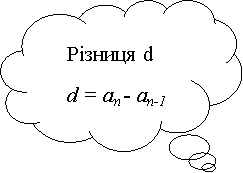
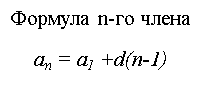
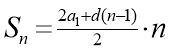
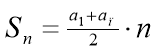
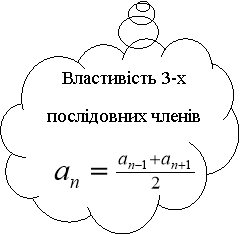
Аналогічно  пригадаємо і повторимо терміни і поняття, що асоціюються у вас з «геометричною прогресією».

А що ж таке геометрична прогресія?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

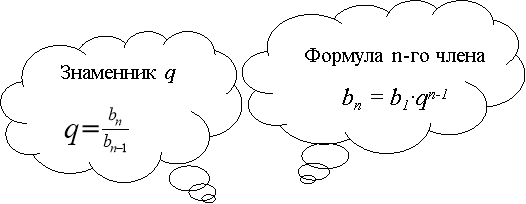
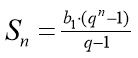
6. Узагальнення і систематизація навичок і вмінь

Ми повторили терміни і формули, а тепер переходимо до узагальнення і систематизації практичних навичок.

Ви отримали випереджуюче завдання: об’єднавшись у три групи, підготувати домашній проект на тему: «Цікаві задачі на прогресії».

 

 

 

 

I група

Учениця. Наша група підготувала проект «Задача про поливання городу» (демонструє презентацію).

Задача

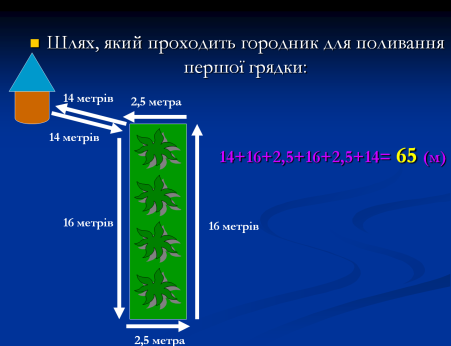
      На городі 30 грядок, кожна довжиною 16 метрів і шириною 2,5 метра. Поливаючи грядки, городник носить відра з водою з колодязя, розміщеного на відстані 14 метрів від краю городу, і обходить  грядки по межі, причому води, яку він приносить за один раз, вистачає для поливання однієї грядки.

        Якої довжини шлях повинен пройти городник, поливаючи весь город? Шлях починається і закінчується біля колодязя.

Вчитель. Розв’язок задачі запишіть у зошити.

Розв’язання

Учениця 1. Отже, є 30 грядок довжиною 16 м і шириною 2,5 м та відстань від колодязя 14 м.

       

 

 

 

 

 

 

 

 

 

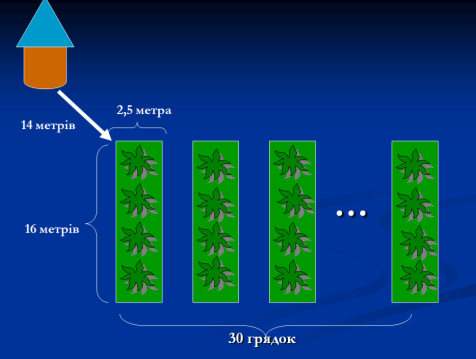
Обчислимо шлях, який городник для поливання першої грядки:

14 + 16 + 2,5 + 16 +2,5 + 14 = 65 (м)

 

 

 

 

 

 

 

 

 

 

При поливанні другої грядки він проходить:

14 + 2,5 + 2,5 +16 +2,5 +16 + 2,5 + 14 = 65 + 5 = 70  (м)

 

 

 

 

 

 

 

 

 

 

Кожна наступна грядка потребує шляху на 5 метрів більше від попередньої. Отримали арифметичну прогресію:

   65; 70; 75; ... ; 65+5∙29.

У цій прогресії  а₁=65; d=5; n=30.

Щоб знайти весь шлях, потрібно обчислити суму  членів цієї прогресії.

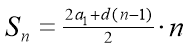Використаємо формулу суми перших n членів арифметичної прогресії:

 

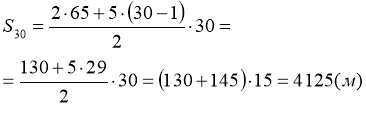Підставимо відомі елементи у формулу:

 

 

 

Отже, городник при поливанні всього городу проходить шлях 4 кілометри 125 метрів.

Відповідь. 4,125 км.

II група

Учениця 2. Наша група підготувала задачу із стародавнього   підручника  — „Арифметики ” Магницького.

Задача

Продавець продав коня за 156 карбованців. Але покупець, купивши коня, передумав і повернув його господарю, кажучи:

•      Нема мені користі купувати за таку ціну коня, який таких грошей не вартий.

Тоді продавець запропонував інші умови:

— Якщо, на твою думку, ціна коня надто висока, то купи лише цвяхи, що у його підковах, а коня одержиш тоді на додачу безкоштовно. Цвяхів у кожній підкові — 6. За перший цвях дай мені лише копійки, за другий — копійки, за третій — 1 копійку, за четвертий — 2 копійки і т.д.

Покупець, спокусившись низькою ціною та бажаючи безкоштовно придбати коня, прийняв умови, думаючи, що за цвяхи доведеться заплатити не більше 10 карбованців. Скільки повинен заплатити покупець?

Вчитель. Розв’язок задачі запишіть у зошити.

Розв’язання

Учениця 2. Спочатку підрахуємо кількість цвяхів. Оскільки підков є чотири, а у кожній — по 6 цвяхів, то всього їх є 24.

За кожен цвях він повинен відповідно заплатити:

 ; ;  1;  2; 2²; 2³; … ; 2^24-3 копійок.

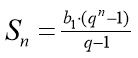Отримали геометричну прогресію, у якій b₁ =; q = 2; n = 24.

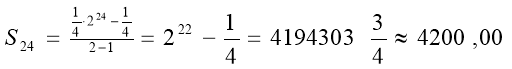Тоді використаємо формулу                        .        Підставивши дані, отримаємо:

                                                                                               (крб.)

Отже, покупець повинен заплатити приблизно 42000 крб. Ось до чого може привести незнання математики!

III група

Учениця 3. Шахи — одна із найдавніших ігор. Щоб зрозуміти легенду, досить знати, що гра відбувається на дошці, поділеній на 64 клітинки. Шахову гру вигадали в Індії, і коли цар Шерам ознайомився з нею,він був у захваті. Наказав привести винахідника Сету, щоб особисто нагородити його.

Ось як це відбувалося.

(Інсценівка)

Цар. Я — цар Шерам, навчився грати в шахи й вражений їх дотепністю. Я бажаю гідно нагородити тебе, Сету. Проси все, що побажаєш, і ти це одержиш.

Сета. Я не впевнений, чи зможеш ти виконати будь-яке бажання, о найвеличніший із царів.

Цар. Я — цар Шерам — найбагатший з усіх царів, проси все, що завгодно!

Сета. Повелителю, накажи видати мені за першу клітинку шахівниці одну пшеничну зернину.

Цар. Одну пшеничну зернину?

Сета. Так володарю. За другу клітинку накажи дати дві зернини, за третю — 4 зернини, за четверту — 8 зернин, і так аж до 64-ї клітинки.

Цар. Як мало ти просиш! Зараз слуги винесуть тобі мішок пшениці.

Учениця 3. Але не вмів цар добре рахувати.

( Розв’язок задачі  учні записують у зошити)

Розв’язання

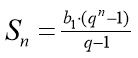
Розглянемо послідовність: 1; 2; 4; 8; 16; … — геометрична прогресія. У ній: b₁ =1; q = 2; n = 64. Тоді

 

Чи велике це число?

 

Це число читається так: 18 квінтільйонів 746 квадрильйонів  73 мільярди 709 мільйонів 551тисяча 615.

Виходить Сета:

Пустелі, гори й океани

Якби засіяти цар зміг,

Років за п’ять спромігся б він

Мені обіцяне віддати.

Вчитель. Молодці. Всі групи підготували цікаві задачі, а тепер колективно розв’яжемо таке завдання:

(Умова проектується на екран за допомогою проектора)

 

 

 

 

 

 

 

Евристична бесіда

• Скільки всього потрібно стержнів?
• Який стержень найдовший?
• Що можна сказати про довжини стержнів від a₁ до a₇ ?
• Як знайти довжину найдовшого  стержня?
• Якою формулою будемо користуватися для обчислення ?
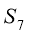• Як знайти суму довжин всіх стержнів?

(Один учень розв’язує  задачу біля дошки).

Розв’язання

а₁ = 5; d = 2

a_n = a₁ +d(n-1)

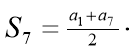
a₇ = 5 +2∙6= 17 (дм)

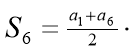
                         7 =                ∙ 7 = 11∙ 7 = 77 (дм)

                              6 =             ∙ 6 = 10∙6 = 60 (дм)

                              77 + 60 = 137(дм)

Відповідь.13 м 7 дм.

Вчитель. Ми розв’язали кілька прикладних задач, а тепер попрацюємо усно над вправою «Незакінчене речення». Правильна відповідь — 2 бали.

(Учні розглядають завдання, що проектуються на дошку).

1. Числова послідовність 4; 8; 16; 32; …  є ….
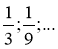2. Різниця арифметичної прогресії 0,5; 1; 1,5; 2; ... дорівнює ...
3. Наступний член геометричної прогресії             дорівнює ...
4. Знаменник геометричної прогресії 2; 6; 18; 54; ... дорівнює ...
5. Для арифметичної прогресії 22; a₂; 40; ...        a₂ = ...
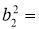6. Числа, кратні 5 утворюють ...
7. Для геометричної прогресії   -3; b₂; -300; ...             …
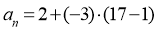8. У геометричній прогресії b₁= 3,5;  q=2;  b₃= ...
9. Формула n-го члена арифметичної прогресії

задає ... член

10.  Наступний член арифметичної прогресії   6,5; 8; ...  дорівнює ...

7. Підсумок уроку

Вчитель. Підведемо підсумок. Чи справдилися ваші сподівання? Де ж використовуються прогресії?

Крім задач, які ми сьогодні розглядали, геометрична прогресія застосовується для стандартизації металорізального інструменту, в банківській справі під час нарахування відсотків на кредит. Навіть зростання площі місячного диска у перші 5 днів відбувається за законами геометричної прогресії.

Оцінювання учнів.

Дякую за сумлінну працю.