Конспект уроку "Вписані і описані чотирикутники"

Конспект уроку

Геометрія

8 клас

Тема: Вписані і описані чотирикутники.

Мета: Сформувати означення чотирикутника, вписаного у коло і чотирикутника, описаного навколо кола; ознайомити учнів із властивістю кутів вписаного чотирикутника та властивістю сторін описаного чотирикутника; ознайомити учнів з розміщенням центрів вписаного і описаного кіл; розвивати математичне мислення та уяву.

Тип уроку: вивчення нового матеріалу.

Обладнання: лінійка, циркуль.

 

Хід уроку

І. Організаційний етап. Оголошення теми уроку. (1 хв.)

ІІ. Актуалізація опорних знань. (3 хв.)

(фронтальне опитування)

1. Яке коло називається описаним навколо трикутника?
2. Яке коло називається вписаним в трикутник?
3. Де лежать центри вписаного і описаного кіл?
4. Чи можна описати коло навколо довільного трикутника (вписати коло в трикутник)?
5. Сформулюйте властивість дотичних, проведених до кола з однієї точки.
6. Який кут називається вписаним в коло?

 

IV. Вивчення нового матеріалу. (20 хв.)

В: Подивіться уважно на дошку, як ви думаєте, який з цих чотирикутників є вписаним?

    

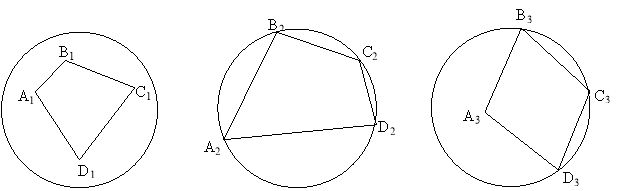
У: A₂B₂C₂D_2.

В: Як можна сказати, який чотирикутник називається вписаним в коло?

У: Чотирикутник називається вписаним в коло, якщо всі його вершини лежать на цьому колі

В: А саме коло називається описаним навколо чотирикутника.

В: А де знаходиться центр описаного кола? Чи буде все так само як і для чотирикутника?

У: Так. Центр описаного кола лежить в точці перетину серединних перпендикулярів, проведених до сторін чотирикутника.

В: Центр описаного кола – точка, рівновіддалена від усіх вершин чотирикутника. Відстань від центру кола до будь-якої вершини кола є радіусом.

 

В: Тепер перейдемо до описаного чотирикутника. Подивіться уважно на дошку, як ви думаєте, який з цих чотирикутників є описаним?

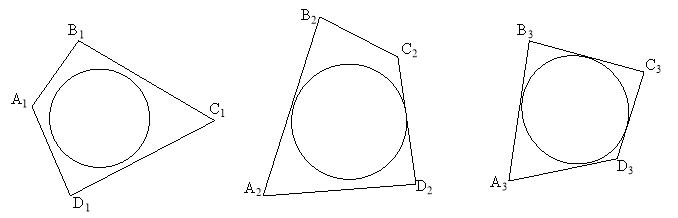
У: A₃B₃C₃D₃.

В: Як ви думаєте, означення описаного чотирикутника буде таким самим як означення описаного трикутника?                           

У: Так. Чотирикутник називається описаним навколо кола, якщо всі його сторони дотикаються до цього кола

В: А саме коло – вписаним у чотирикутник.

В: Де знаходиться центр описаного кола?

У: Центр вписаного кола лежить в точці перетину бісектрис кутів чотирикутника.

В: Відстань від центра кола до будь-якої точки дотику сторони до кола є радіусом.

 

В: Чи можна описати коло навколо довільного чотирикутника (вписати коло в чотирикутник)?

У: Так.

В: Насправді неможна. Давайте з’ясуємо, коли чотирикутник можна вписати в коло.

(Учні записують в зошитах)

Теорема 1. Сума протилежних кутів вписаного чотирикутника дорівнює 180 ^о.

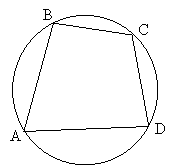
Дано: ABCD – чотирикутник, вписаний в коло.

 

Довести: А+С=180^о,В+D=180^о.

 

Доведення

Нехай чотирикутник АВСD вписаний у коло.

В: Яким є А ?

У: Вписаним?

В: Що ми знаємо про вписаний кут?

У: Дорівнює половині дуги, на яку спирається.

А=1/2BCD, C=1/2DAB. Тоді А+С=1/2(DСB+DАB)= 1/2∙360^о=180^о

В: Чому рівна сума всіх кутів чотирикутника?

У: 360 ^о.

В: А сума кутів А і С?

У: 180 ^о.

Тоді B+D=180^о.

Доведено.

 

В: З цієї властивості випливає наступна ознака вписаного чотирикутника і наслідки.

Теорема 2. Якщо в чотирикутнику сума двох протилежних кутів дорівнює 180^о, то навколо такого чотирикутника можна описати коло.

Наслідок 1. Навколо кожного прямокутника можна описати коло. Якщо паралелограм вписаний у коло, то він є прямокутником.

Наслідок 2. Навколо кожної рівнобічної трапеції можна описати коло. Якщо трапеція вписана в коло, то вона рівнобічна.

 

В: Тепер з’ясуємо, коли чотирикутник можна описати навколо кола.

(Учні записують в зошитах)

Теорема 3. Суми протилежних сторін описаного чотирикутника рівні.

Дано: ABCD – чотирикутник, описаний навколо кола

K, L, M, N – точки дотику.

 

Довести: АВ+СD=ВС+АD.

 

Доведення

В: Що ми маємо за властивістю дотичних, проведених до кола з однієї точки?

У: АK=АN, ВK=ВL, CL=CM, DM=DN.

В: Як ми можемо записати сторону АВ?

У: АВ=АK+ ВK.

В: А сторону СD ми можемо так само записати?

У: Так, СD=CM+DM.

В: А тепер розглянемо суму цих сторін:

АВ+СD= АK+ ВK+ CM+DM=…

А згідно рівностей, записаних вище:

…= АN+ВL+CL+DN=BC+AD.

Доведено.

 

В: З цієї властивості випливає наступна ознака описаного чотирикутника і наслідки.

Теорема 4. Якщо в чотирикутнику суми протилежних сторін рівні. То в цей чотирикутник можна вписати коло.

 

Наслідок 3. У будь-який ромб можна вписати коло. Якщо в паралелограм вписано коло, то він є ромбом.

 

V. Закріплення нового матеріалу. (15 хв.)

Розв’язування вправ.

№252. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Визначте, чи можна описати коло навколо чотирикутника ABCD, якщо кути A, B, C, D дорівнюють відповідно:

а) 90^о, 90^о, 20^о, 160^о;

б) 5^о, 120^о, 175^о, 60^о.

Розв’язання:

а) 90^о+20^о =110^о ні

б) 5^о +175^о =180^о, 120^о +60^о =180^о  так

 

№253. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Знайдіть невідомі кути:

а) вписаного чотирикутника, якщо два його кути дорівнюють 46^о і 125^о.

б) вписаної трапеції, якщо один з її кутів дорівнює 80^о.

Розв’язання:

а) Нехай A=46^o , В=125^о (С125^о, бо 46^o+125^о180^о).

     С=180^о-A=180^о-46^о=134^о.  D=180^о-B=180^о-125^о=55^о.

 

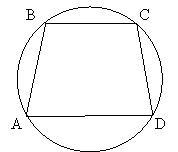б)                           

Дано: ABCD – вписана трапеція, А=80^о.

 

Знайти: B, C, D.

 

 

 

      

Розв’язання:

В: Яка має бути трапеція, щоб її можна було вписати в коло?

У: Рівнобічна.

В: А якими є кути при основах в такій трапеції?

У: Рівні. А=D==80^о.

B=С=180^о-A=180^о-80^о=100^о.

Відповідь: 100^о,  80^о, 100^о.

 

 

№260. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Радіус кола, вписаного у квадрат, дорівнює 3 см. Знайдіть периметр квадрата.

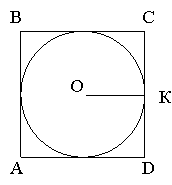
Дано:

ABCD – квадрат описаний навколо кола, R=3 см.

 

Знайти: Р_ABCD

 

 

 

 

Розв’язання:

OK=R.

В: Чому рівний периметр квадрата?

У: Сумі всіх сторін.

В: А в квадрата сторони якими є?

У: Рівними між собою. Р_ABCD= 4АВ.

BC=2OK=23=6 (см)

Р_ABCD= 4BC=46=24 (см)

Відповідь: 24 (см).

 

№261. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Чотирикутник ABCD вписаний у коло, центр якого лежить на стороні AD. Знайдіть кути чотирикутника, якщо ACB=20^o, DBC=10^o.

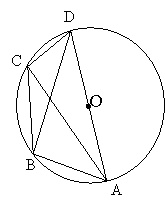
Дано: ABCD-чотирикутник вписаний в коло, ACB=20^o, DBC=10^o.

 

Знайти: A, B, C, D.

 

 

Розв’язання

В: Чому дорівнює кут, що спирається на діаметр?

У: 90^о.

В: А ми маємо тут кути, що спираються на діаметр?

У: Так, ACD=90^o, ABD=90^o.

C=ACB+ACD=20^o+90^o=110^o.

B=DBC+ABD =10^o+90^o=100^o.

A=180^о-C=180^о-110^о=70^о.

D=180^о-B=180^о-100^о=80^о.

Відповідь: 70^о, 100^о, 110^о, 80^о.

 

VІ. Підсумки уроку. (2 хв.)

1.   Який чотирикутник називається вписаним в коло? Описаним навколо кола?
2.   Сформулюйте теорему про властивість кутів вписаного чотирикутника.
3.   Сформулюйте теорему про властивість сторін описаного чотирикутника.
4.   Сформулюйте ознаку вписаного чотирикутника (описаного чотирикутника).

 

VIІ. Домашнє завдання. (1 хв.)

Вивчити §8 (Пункти 8.1, 8.2) .

Розв’язати №254, 257, 259.