Конспект уроку "Вписані і описані чотирикутники. Самостійна робота. Розв’язування задач."

Конспект уроку

Геометрія

8 клас

Тема: Вписані і описані чотирикутники. Самостійна робота. Розв’язування задач.

Мета: закріпити знання учнів про вписані й описані чотирикутники, застосувати властивості сторін описаного чотирикутника та кутів вписаного чотирикутника при розв’язуванні задач.

Тип уроку: відпрацювання вмінь та навичок, діагностика засвоєння.

Обладнання: лінійка, циркуль, роздатковий матеріал.

 

Хід уроку

І. Організаційний етап. Оголошення теми уроку. (1 хв.)

 

ІІ. Перевірка домашнього завдання. (3 хв.)

В: Які проблеми виникли у вас при розв’язуванні домашнього завдання? Давайте спробуємо їх вирішити.

Вчитель викликає до дошки учня, у якого виникла проблема.

 

ІІІ. Актуалізація опорних знань. (5 хв.)

Запитання до класу.

(Учні відповідають по бажанню)

1. Сформулюйте теорему Фалеса.
2. Що таке середня лінія трикутника, яку властивість має середня лінія?
3. Чому рівна градусна міра дуги?
4. Що таке вписаний кут і чому він дорівнює?
5. Сформулюйте властивість і ознаку вписаного чотирикутника.
6. Сформулюйте властивість і ознаку описаного чотирикутника.
7. Які наслідки з даних теорем ви знаєте?

 

IV. Відпрацювання вмінь. (35 хв.)

В: Сьогодні ми почнемо урок з невеличкої самостійної роботи.

(Вчитель роздає завдання на картках)

Самостійна робота

I варіант

1.          Суми протилежних сторін чотирикутника дорівнюють 34 см і 36 см . Чи можна у цей чотирикутник вписати коло? Чому?
2.          Два сусідні кути чотирикутника дорівнюють 120⁰ і 150⁰. Знайдіть решту кутів чотирикутника, якщо його можна вписати в коло.
3.          Периметр чотирикутника ABCD, описаного навколо кола, дорівнює

36 см. AB=10 см, CD=8 см, BC=AD. Знайдіть сторони BC і AD.

II варіант

1.          Суми протилежних сторін чотирикутника дорівнюють 54 см і 54 см . Чи можна у цей чотирикутник вписати коло? Чому?
2.          Два кути чотирикутника дорівнюють 100⁰ і 130⁰. Знайдіть решту кутів чотирикутника, якщо його можна вписати в коло.
3.          У чотирикутнику ABCD AB=10 см, BC=8 см, CD=7 см. Якої довжини має бути сторона AD, щоб цей чотирикутник можна було описати навколо кола?

 

(Один з учнів працює біля дошки, інші в себе в зошитах, хто першим розв’яже самостійно вчитель ставить оцінку і пропонує наступну задачу)

№1. Різниця периметра рівностороннього трикутника і його середньої лінії дорівнює 15 см. Знайдіть сторону даного трикутника.

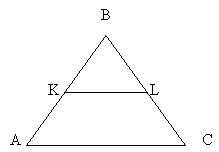
Дано: ABC – рівносторонній, - KL=15 см,

Знайти: AB.

 

Розв’язання

В: Який трикутник дано в умові?

У: Рівносторонній.

В:Правильно, а що ви знаєте про рівносторонній трикутник?

У: В ньому всі сторони рівні.

В: А якби ми позначили сторони через х: AB=BC=AC=x (см). То як би записався периметр?

У: =3x (см).

В: А його середня лінія?

У: KL= x.

В: Чи могли би ви записати рівність дану в умові через х?

У: 3x - x =15;

В: Розв’яжемо це рівняння:          

У: 3x - x =15; 2 x =15, то x =15; 5x =215; x = ; x =6(см.)

Відповідь: 6 см.

 

№2. На рис.1 = , О=12. Знайдіть периметр трикутника .

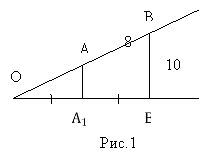
Дано: =, О=12, О= , АВ=8, ВВ₁=10.

Знайти: .

 

Розв’язання

В: Що треба знайти, щоб обчислити ?

У: Знайти всі сторони .

В: Скільки дорівнює О?

У: О= = ОВ₁ = 12=6.

В: Подивимось на рисунок, за умовою =, то що можна сказати про розміщення прямих?

У: То А В.

В: А чому?

У: Бо і відповідні.

В: А якщо А В і  О= , то ми можемо сказати про ОА і АВ?

У: Рівні: ОА= АВ=8.

В: А чому?

У: За теоремою Фалеса.

В: Ми чи можемо тепер знайти АА₁?

У: Так, бо вона є середньою лінією.

В: Правильно.

У: АА₁= ВВ₁= 10=5.

В: Скільки дорівнює О?

У: О= = ОВ₁ = 12=6.

В: Тепер ми вже можемо знайти ?

У: Так, =ОА+АА₁+ ОА₁=8+5+6=19.

 

№ 3. Знайдіть кути рівнобедреного трикутника, основа якого стягує п’яту частину дуги описаного кола. Розгляньте всі можливі випадки.

 

Дано: ABC – рівнобедрений, CmB==72^о.

Знайти: А, В, С.

Розв’язання

В: Давай те з’ясуємо, де будуть лежати вершини рівнобедреного трикутника, вписаного в це коло з даною основою.

 

 

 

 

 

Випадок 1. (Див. рис.1)

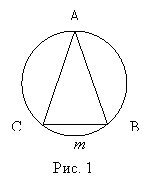В: Чому дорівнює А?

У: А=CmB=72^о=36^о (як кут, що спирається на CmB)

В: Як обчислити А і В?

В: Чому дорівнює сума кутів трикутника?

А+В+С=180^о. В+С=180^о-А=180^о-36^о=144^о.

В: А який в нас ABC?

У: Рівнобедрений. В=С=144^о=72^о.

 

Відповідь: 36^о, 72^о, 72^о.

 

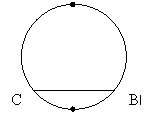
Випадок 2. (Див. рис.2)

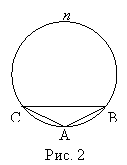В:Чому дорівнює градусна міра CnB?

У: CnB=360^o -CmB=360^о-72^о=288^о.

В: Далі можна розв’язати аналогічно до попереднього.

А=CnB=288^о=144^о (як кут, що спирається на дугу)

А+В+С=180^о.

В+С=180^о-А=180^о-144^о=36^о.

В=С=36^о=18^о

Відповідь: 144^о, 18^о, 18^о.

 

№4. Доведіть, що радіус кола, вписаного в прямокутну трапецію, дорівнює різниці середньої лінії і половини більшої бічної сторони.

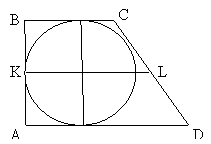
Дано: ABCD – прямокутна трапеція, описана навколо кола.

Довести: R=KL - .

 

Доведення

В: Яку властивість має описаний чотирикутник?

У: Суми протилежних сторін рівні AB+CD=BC+AD.

В: Чи можна виразити BC+AD через середню лінію?

У: Так, BC+AD=2KL.

В: Чи можна виразити суму AB і CD через радіус?

У: AB+CD=2R+CD.

В: Ліві частини підкреслених рівностей рівні, то рівними будуть і праві частини. Запишемо це.

У: 2R+CD=2KL.

R=KL - .

Доведено.

 

V. Домашнє завдання. (1 хв.)

Повторити § 6, 7, 8.

Розв’язати задачі на сторінці 87 №№ 2, 3, 6.