Конспект уроку "Вписані і описані чотирикутники. Розв’язування задач."

Конспект уроку

Геометрія

8 клас

Тема: Вписані і описані чотирикутники. Розв’язування задач.

Мета: закріпити знання учнів про вписані й описані чотирикутники, застосувати властивості сторін описаного чотирикутника та кутів вписаного чотирикутника при розв’язуванні задач; розвивати математичне мислення та уяву.

Тип уроку: відпрацювання вмінь та навичок.

Обладнання: лінійка, циркуль.

 

Хід уроку

І. Організаційний етап. Оголошення теми уроку. (2 хв.)

ІІ. Перевірка домашнього завдання. (5 хв.)

В: Які проблеми виникли у вас при розв’язуванні домашнього завдання? Давайте спробуємо їх вирішити.

Вчитель викликає до дошки учня, у якого виникла проблема.

 

№ 254. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Знайдіть невідомі кути:

а) вписаного чотирикутника ABCD, якщо кути A і C рівні, а кут D дорівнює 50^о.

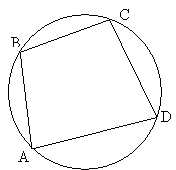
Дано: ABCD – чотирикутник, вписаний в коло.

А=С, D=50^o.

Знайти: А, В, С.

 

Розв’язання:

В: Що нам відомо про суму кутів A і C?

У: Дорівнює 180^о.

 

В:  Якщо А=С, то як ми можемо записати цю суму?

У: А+С=А+А=2А=180^о.

С=А==90^о.

В: Тепер як знайти В?

У: В=180^о-D=180^о-50^о=130^о.

В: Ми знайшли всі кути, отже задача розв’язана.

 

б) вписаної трапеції, якщо сума двох з них дорівнює 230^о.

Розв’язання:

В: Що ми знаємо про трапецію, вписану в коло?

У: Вона рівнобічна.

В: А що ми знаємо про кути в рівнобічній трапеції?

У: При основах рівні.

В: Чому дорівнює сума кутів трапеції, прилеглих до однієї бічної сторони?

У: 180^о.

В: А протилежних кутів вписаного чотирикутника?

У: 180^о.

В: Отже, задача розв’язку не має.

 

№ 257. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

В опуклому чотирикутнику АBCD A+C=B+D. Доведіть, що навколо цього чотирикутника можна описати коло.

Розв’язання

В: Чому дорівнює сума кутів чотирикутника?

У: 360^о.

В: То чому тоді буде дорівнювати сума A+C, якщо A+C=B+D?

У: A+C=B+D==180^о.

Відповідь: Доведено.

 

ІІІ. Актуалізація опорних знань. (5 хв.)

Запитання до класу.

(Учні відповідають по бажанню)

1. Сформулюйте властивості кутів вписаного чотирикутника.
2. Сформулюйте властивості сторін описаного чотирикутника.
3. Чи можна описати коло навколо довільного:

1.   прямокутника;
2.   квадрата;
3.   ромба;
4.   трапеції.

Відповідь поясніть.

4. Чи можна вписати коло у довільний:

1.   прямокутник;
2.   квадрат;
3.   ромб;
4.   трапецію.

Відповідь поясніть.

 

IV. Відпрацювання вмінь. (15 хв.)

 (Учень працює біля дошки, хто першим розв’яже самостійно вчитель ставить оцінку і пропонує наступну задачу)

 

№256. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Із точки С, що лежить усередині гострого кута А, проведено перпендикуляри CB і CD до сторін кута. Доведіть, що навколо чотирикутника ABCD можна описати коло.

 

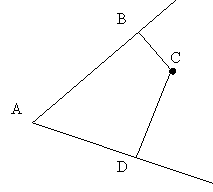
Дано: Точка C – всередині кута A, CBA=90^o, CDA=90^o.

Довести: навколо чотирикутника ABCD можна описати коло.

 

 

 

 

Доведення

В: Згадаймо, коли навколо чотирикутника можна описати коло.

В: Як розв’язати цю задачу?

У: Перевірити чи сума протилежних кутів трикутника дорівнює 180^о.

B+D=90^o+90^o=180^о (за умовою).

А+С =360^о-(B+D)=360^о-180^о=180^о.

Відповідь: Доведено.

 

№268. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Діагональ ромба, що виходить із вершини кута 60^о, дорівнює 24 см. Знайдіть радіус кола, вписаного в ромб.

(З’ясовуємо, що дано і що потрібно знайти)

 

 

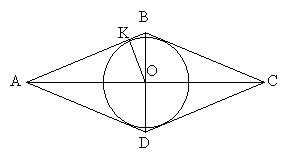Дано: ABCD – ромб, описаний навколо кола, AC=24 см, BAD=60^o.

Знайти: R.

 

 

 

Розв’язання

В: Де лежатиме центр вписаного в ромб кола?

У: В точці перетину діагоналей.

В: Зобрази шуканий радіус на малюнку і заданий кут.

В: З якого трикутника можна знайти радіус?

У: ОКВ і ОКА.

В: А яку властивість мають діагоналі ромба?

У: Перетинаються під прямим кутом і в точці перетину діляться навпіл.

AO=AC=24=12 (см)

В:  А чи можемо ми знайти OAB.

У: Можемо, OAB=DAB=60^o=30^o.

В: Давайте розглянемо AKO. Що ми в ньому маємо?

У: OKA=90^о, бо це кут, що утворює дотична і радіус. Отже, AKO – прямокутний.

В: А чому дорівнює ОК, якщо він лежить проти кута 30^o.

У: OK=AO=12=6 (см)

Відповідь: 6 см.

 

№270. (Єршова А.П., Голобородько В.В., Крижановський О.Ф., Єршов С.В.)

Середня лінія рівнобедреного трикутника, паралельна основі,ділить даний трикутник на трапецію і трикутник із периметром 24 см. Основа даного трикутника дорівнює 12 см. Доведіть, що в отриману трапецію можна вписати коло.

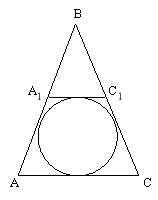Дано: ABC – рівнобедрений з основою AC, AC=12 см,

А₁С₁ – середня лінія, =24 см,

Довести: В трапецію АА₁С₁С можна вписати коло.

 

Доведення

В: Коли в чотирикутник можна вписати в коло?

У: Якщо суми протилежних сторін ріні між собою.

В: Тому треба знайти суми сторін АС і А₁С₁, АА₁ і СС₁ та порівняти їх.

В: Що ми знаємо про середню лінію трикутника?

У: Паралельна одній зі сторін трикутника і дорівнює половині цієї сторони.

А₁С₁=АС=12=6 (см).

АС+А₁С₁=12+6=18 (см).

В: А яким є трикутник А₁ВС₁?

У: Рівнобедреним.

В: Так, тому з того, що ми сказали, що можна записати?

У: А₁В=ВС₁.  =А₁В+ВС₁+А₁С₁=24 (см).

А₁В+ВС₁=24-6=18, А₁В=18=9 (см).

В: А як середня лінія ділить сторони трикутника?

У: Навпіл. АA₁=А₁B=9 см. СС₁=С₁В=9 см.

В: Знайдемо суму АА₁ і СС₁.

У: АА₁+СС₁=9+9=18 (см).

В: Ми маємо усі сторони трапеції, то чи можна в неї вписати коло?

У: Так, бо АA₁+СС₁=А₁С₁+АС=18 (см).

Відповідь: Доведено.

 

V. Підсумки уроку. (17 хв.)

 

VI. Домашнє завдання. (1 хв.)

Повторити §8 (Пункти 8.1, 8.2).

Розв’язати №№ 259, 263.