Урок на тему: « Розв’язування задач за допомогою теореми Піфагора

Конспект уроку з геометрії  для  8 класу   на тему:

  « Розв’язування задач за допомогою  теореми Піфагора».

Мета уроку: Узагальнити та систематизувати знання учнів з теми; показати різні способи доведення теореми Піфагора; вдосконалювати вміння та навички учнів застосовувати теорему Піфагора при розв’язуванні задач;

розвивати логічне мислення учнів, стимулювати їх пізнавальну діяльність, інтерес до математики.

Тип уроку. Урок  формування знань та вмінь

Обладнання: комп’ютер, проектор.

Програмне забезпечення: презентація «Теорема Піфагора. Розв’язування задач на застосування теореми Піфагора» 

                                                     Геометрія володіє двома скарбами:

                                  один із них – це теорема Піфагора,

                 а другий – поділ відрізка в

      середньому і крайньому  відношенні.

                                                       Перший можна порівняти  з   мірою  золота, а другий більше нагадує

                                                        коштовний камінь.

Йоганн Кеплер.

                              німецький астроном і математик

 

                 План уроку.

 I.Організаційна частина.

II.Мотивація навчальної діяльності. Оголошення теми уроку.

III. Актуалізація опорних знань у

 1.Фронтальне опитування

 2.Усний рахунок.

 IV.  Застосування набутих знань

  1. Виконання  задачі № 587 а,в.(2б+2б)

 2.Робота в групах.(2б+2б +2б)

Доведення теореми Піфагора.

Розв’язування  задач

 Розв’язування   старовинних задач

 3. Робота в парах. Розгадування кросворду (1 б)

V. Підсумок уроку.

 VI.Оцінювання

VII.Домашня робота

                          Хід уроку

I.Організаційний момент

 II. Мотивація навчальної діяльності. Оголошення теми уроку.

Сьогодні 21 лютого. Учні роблять повідомлення на тему:

Цей день в історії …

Міжнародний день рідної мови.

1784 — Закладене місто Миколаїв.

1993 —У Донецьку Сергій Бубка встановив світовий рекорд у стрибках із жердиною в закритих приміщеннях — 6 м 15 см.

1431 — Розпочався суд над Жанною д'Арк.

  2018-  Проходять зимові олімпійські ігри.

 Учитель. А ви знаєте, що олімпійські ігри вперше  почали проводитись у Стародавній Греції ще до нашої ери. Змагання проводились з бігу на колісницях, кулачного бою. Цього міцного юнака з товстою шиєю та коротким носом, справжнього забіяку, судді  олімпіади не хотіли допускати до змагань, тому що  він  був досить малий на зріст. Казали, що в нього «ні зросту, ні сили, ні зовнішності». «Так, - сказав на це хлопець, - але я буду наносити удари з математичною точністю!» Йому вдалося побитися зі своїми супротивниками, при цьому ще й перемогти. Цим хлопцем був Піфагор, великий математик  . А подія ця відбувалася у 548 році до н.е. на 58 олімпійських іграх. Прославився Піфагор своєю теоремою про відношення сторін у прямокутному трикутнику .Ми її вивчили  і сьогодні на уроці будемо роз’язувати задачі , використовуючи теорему Піфагора.

III.  Актуалізація опорних знань учнів  

 Бліцопитування (швидке фронтальне повторення переглянутого навчального матеріалу)                                 

• Який трикутник називається прямокутним?
• Як називаються сторони прямокутного трикутника?
• Яку сторону називають гіпотенузою?
• Які сторони наз. катетами?
• Чому дорівнює сума гострих кутів прямокутного трикутника?
• Чи може в прямокутному трикутнику бути два прямих кути? Чому?
• Як читаються ознаки подібності прямокутних трикутників?
•  Перпендикуляр ,проведений з вершини трикутника на протилежну сторону абоїї продовження..
• Закінчити речення:Відрізок, що сполучає основу перпендикуляра з основою похилої… 
• Як читається теорема Піфагора?
• Як читається теорема обернена теоремі Піфагора
• Які проекції мають рівні похилі?

 

 

 

                        Усний рахунок                                  

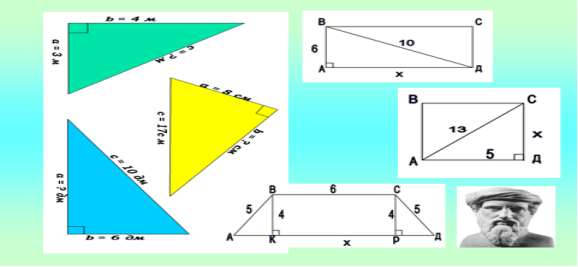
  Учитель.   Ми повторили деякі теоретичні питання курсу геометрії. Але знати математику – це не лише знати теоретичні відомості з тієї чи іншої теми, а і вміти їх застосовувати при доведенні теорем, розв’язуванні задач та вправ. Використовуючи той факт, що квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів катетів, можна довести багато інших теорем і розв’язати чимало різних задач.

IV.Застосування набутих знань.

Учитель.Розв’яжемо задачу №587(а) з підручника.(біля дошки)(2б)

Розв,язання.    У рівнобедреному трикутнику висота, проведена до основи є бісектрисою та медіаною. Отже, утворився прямокутний трикутник  АВД  з катетом  ВД = 20:2=10(см)  і гіпотенузою 26 см.

За т.Піфагора  ВД² =АВ²-АД²  , 26² - 10² =676 – 100 = 576 = 24²

ВД = 24 см.

Відповідь.24 см.

В)самостійно(2б)

25х²=9х²+144, 144= 25х²-9х², 144=16х², х²=144:16, х²=9, х=3. а =в =15см,с=18см.

 Учитель. Цікаво, що у середні віки теорема Піфагора вважалась настільки складною, що її називали pons asinorum («ослячий місток»), або elefuga («втеча нікчемних»), оскільки далеко не кожний міг її довести, тобто перейти через «ослячий місток».

Сьогодні ми успішно вивчаємо і використовуємо цю історичну теорему при розв’язуванні різних задач.

  Далі попрацюємо в групах.

1.Група.  Школа Піфагора.

  2.Група.Школа Евкліда.

 3.Група.Школа Чу Пей

 4.Група.Школа Бхаскари.

Відомо понад 300 різних доведень цієї теореми. Ще з давніх часів люди шукали і знаходили різні способи, і до цього часу знаходять все нові і нові доведення теореми Піфагора.    

  Виступи учнів, які готували різні  способи доведення теореми. (2б)             

1.Школа Піфагора.

Доведемо теорему Піфагора, використовуючи властивість подібних трикутників.

Доведення.

 

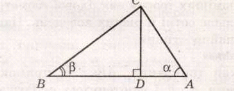
У трикутнику ABC (<C = 90°)  проведемо CD перпендикулярно AВ . Утворились подібні трикутники ABC і ACD.

За властивістю подібних трикутників їх сторони пропорційні, тобто

АВ: АС = АС: AD,

AC² = AB · AD. (1)

Трикутники ABC і CBD мають рівні кути, вони подібні. Сторони цих трикутників пропорційні, тобто:

АВ: СВ = СВ: DB,

CB² = AB · DB. (2)

Додамо почленно рівності (1) і (2):

AC² + СВ² = AB· AD + AB  · DB,

AC² +CB² =AB(AD + DB),

AC² + CB² = AB ·AB,

AC² +CB² = AB², що й потрібно було довести.

 2.Школа Евкліда

В книзі «начало» Евклід довів теорему Піфагора.

Площа квадрата, побудованого на гіпотенузі прямокутного трикутника, дорівнює сумі  площ квадратів , побудованих на його катетах. Відео.

     Така ілюстрація до теореми здається подібною до штанів, тому і маємо жартівливі примовки: «Піфагорові штанці рівні є в три кінці», «Пифагоровы штаны на все стороны равны». Якщо цей рисунок повернути , то вбачатимемо  не штани, а сорочку, тому примовляють: «Хто в сорочці Піфагора – піднімає руки вгору». 

3.Школа Гугу

В Стародавньому Китаї було доведено теорему Піфагора .

 

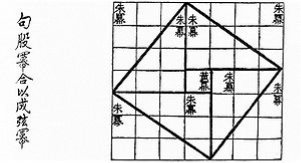
Написана десь між 500 до н. е. і 200 до н. е., китайська математична книга «Чу Пей» (周髀算经) дає візуальне доведення теореми Піфагора, яка в Китаї називається теорема Гугу (勾股定理), для трикутника із сторонами (3, 4, 5). Під час правління династії Хань, з 202 до н. е. до 220 н. е. Піфагорові трійки з'являються в книзі «Дев’ять розділів математичного мистецтва» разом із згадкою про прямокутні трикутники.
 

 4.Школа Бхаскари.

У своїй праці «Вінок систем» індійський математик Бхаскара наводить приклад дове­дення теореми Піфагора у вигляді креслення з підписом «Дивись!».  Використаємо креслення Бхаскари для доведення теореми.

                                        

Доведення.

Площа квадрата, побудованого на гіпотенузі с трикутника, дорівнює сумі площ чотирьох прямокутних трикутників і квадрата, довжина сторони якого — (а-b). Тобто

с² = + (а - b)² = 2ab + а² - 2ab + b² = а² +b².

Отже, а²+b² = с².

 Учитель. Розв’язування задач на застосування теореми Піфагора (робота в групах, учні об’єднані в групи, які працюють в режимі «демократії»:  розв’язують задачу і вибирають учня, який пояснює розв’язок)

Задача 1  (2б)                                                            

У рівнобічній трапеції основи дорівнюють 7см і 13 см, а висота дорівнює 4см. Знайдіть бічну сторону трапеції. Відповідь.5см.

   Задача 2  (2б)                                                        

Основа АD рівнобічної трапеції АВСD ділиться висотою ВЕ на відрізки довжиною 5см і 16см, а довжина бічної сторони трапеції 13см. Знайти діагоналі трапеції. Відповідь.20см

  Задача 3  (2б)                                                          

Дано прямокутну трапецію, у якої бічні сторони дорівнюють 17дм і 15дм, а менша основа – 9дм. Знайти середню лінію трапеції.

Відповідь.13см

                   Задача 4  ( 2б)                                                          

Висоти двох вертикальних стовпів дорівнюють 5м і 12,5м. Відстань між ними 10м. Знайти найменшу довжину троса, яким можна з’єднати верхні кінці цих стовпів.

Відповідь.12,5см

Учитель. Розв’язування старовинних задач на застосування теореми Піфагора.

1.Школа Піфагора.    (2б)                                                      

Старовинна задача з підручника Арифметика Леонтія Магніцького. Сталося якомусь чоловіку до стіни драбину поставити , стіни ж тої висота є 117 стоп .І відати хоче він , на скільки стоп драбини нижній кінець від стіни отстояти має , якщо драбини довжина 125 стоп .

2.Школа Евкліда.       (2б)                                              

Дах будинку має форму рівнобедреного трикутника ( АВС) , АВ=50м ,основа трикутника АС = 96м . Знайти висоту даху .

 3.Школа  Гугу        (2б)                           

Висота новорічної ялинки 8 м. Для закріплення її у вертикальному положенні від вершини ялинки зробили натяжки АВ, АВ1, АВ2 однакової довжини і закріпили їх на підлозі на відстані 6 м від основи ялинки. Якої довжини повинна бути натягуюча проволока, щоб ялинка стояла вертикально.

4.Школа Бхаскари      (2б)

На березі річки тополя росла

І вітру порив її стовбур зламав .

Тополя упала і стовбур її

Кут прямий з течією річки утворив .

Пам’ятай , в тому місці ріка

Чотири фути була шириною .

Верхівка схилилась до краю ,

Залишивши три фути всього над водою .

Прошу , тепер швидше скажи мені ти :

Тополя якої була висоти ?

 3.Робота в парах.                                                                      

Розгадування кросворду.(1б)

 

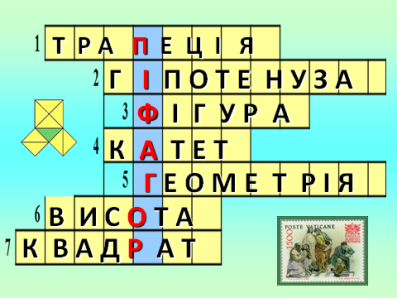
1.Чотирикутник, у якого дві сторони паралельні, а дві інші – не паралельні .                                    (Трапеція)

 2.Найбільша із сторін прямокутного трикутника. (Гіпотенуза)

 3.Трикутник – це ..., яка складається із трьох точок, що не належать

  одній прямій, і трьох відрізків, попарно з’єднуючих ці точки. (Фігура)

4.Одна із сторін трикутника, що утворюють прямий кут. (Катет)

5.Наука, яка вивчає властивості геометричних фігур. (Геометрія)

6.Перпендикуляр, проведений із вершини трикутника на протилежну

    сторону. (Висота)

  7.Прямокутник, у якого всі сторони рівні.    (Квадрат)

 V. Підсумок уроку.

V1.Оцінювання.Максимальна кількість балів 11.За активність на уроці додати 1б.

  V11. Домашнє завдання.

Початковий рівень

№593.повторити п.13.

Достатній рівень.

№ 640,643.

Високий рівень.

** Знайти медіану рівнобедреного трикутника, проведену до бічної   сторони, якщо бічна сторона і основа трикутника дорівнюють відповідно 30см і 48см

№649.