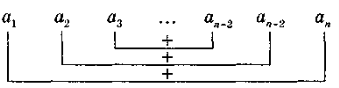Конспект уроку з алгебри 9 клас “Арифметична прогресія”.

Тема: Арифметична прогресія та її застосування

Мета уроку: Ввести поняття арифметичної прогресії, розглянути її властивості; вивести формулу n-го члена та навчити учнів застосовувати її до розв’язування задач; розвивати в учнів вміння відтворювати зміст вивчених понять, а також використовувати їх для розв’язування задач, що передбачають виділення арифметичної прогресії серед інших числових послідовностей, використання властивостей арифметичної прогресії.

 

Цілі:

формування предметних компетентностей:

      -  сформувати поняття арифметичної прогресії;

- домогтися засвоєння властивостей арифметичної прогресії;

- сформувати вміння застосовувати поняття та властивості арифметичної прогресії до розв’язування задач;

     - продовжити подальшу роботу з вироблення вміння порівнювати математичні поняття, знаходити подібності й відмінності, уміння спостерігати, помічати закономірності, проводити міркування за аналогією.

формування ключових компетентностей:

• сприяти усвідомленню цінності нових знань і вмінь;
• формувати вміння доречно та коректно вживати в мовленні математичну термінологію;
• сприяти підвищенню інтересу до математики, активності, умінню спілкуватися, аргументовано відстоювати свої міркування;
• сприяти самовихованню старанності, дисциплінованості.

Тип уроку: засвоєння нових знань і вмінь.

Обладнання та наочність: підручник (Алгебра для 9-го класу авторів А. Г. Мерзляк, В. Б. Полянський, М. С. Якір (2016)), конспект уроку.

 

 

Хід уроку:

І. ОРГАНІЗАЦІЙНИЙ ЕТАП

 Повідомлення теми та мети уроку

Тема уроку – арифметична прогресія. На цьому уроці ми дізнаємося, що таке арифметична прогресія, як відрізнити арифметичну прогресію від інших послідовностей і навчитися розв’язувати задачі з використанням властивостей арифметичних послідовностей.

 

Слово «прогресія» походить від латинського слова «progressio» і означає «рух уперед» (як і слово «прогрес»). Уперше цей термін як математичний вживається у працях римського вченого Боеція (V – VI ст.).

Перша умова, якої треба дотримуватися в математиці, – це бути точним. Друга – бути чітким, і наскільки можливо, простим.

Отже, ми сьогодні з вами на уроці просто, чітко і з легкістю вивчимо тему: «Арифметична прогресія», навчимося обчислювати елементи прогресії, покажемо практичне застосування теми на прикладах історичних задач, задач практичного змісту, будемо удосконалювати вміння оцінювати свої досягнення.

 

ІІ. ПЕРЕВІРКА ДОМАШНЬОГО ЗАВДАННЯ

Вправа «Знайди помилку». Розв'язання домашнього завдання заздалегідь записані вчителем на дошці.

Учні звіряють розв'язання в зошитах із записами на дошці, шукають і виправляють помилки.

 

III. АКТУАЛІЗАЦІЯ ОПОРНИХ ЗНАНЬ ТА ВМІНЬ

1. Інтерактивна вправа «Незакінчені речення».

• Об'єкти, які пронумеровано натуральними числами 1, 2, 3, n, ...

(Утворюють послідовність.)

• Об'єкти, які утворюють послідовність, називають ...

(Членами послідовності.)

• Послідовність називають числовою, якщо …

(Її членами є числа.)

 2. Фронтальне опитування:

1. Як позначаються послідовності і їх члени?
2. Яка послідовність називається скінченною?
3. Яка послідовність називається нескінченною?
4. Які способи задавання послідовностей ви знаєте?

3. Усні вправи

Дано скінченну послідовність: (х_п): 3; 0; -3; -6; -9; -12.

Укажіть:

1) перший, третій, шостий члени цієї послідовності;

2) чи є ця послідовність зростаючою, спадною;

3) формулу її п-го члена.

 

ІV. ВИВЧЕННЯ НОВОГО МАТЕРІАЛУ

Під час розкопок у Єгипті було знайдено папірус, датований 2000 р. до н.е., але виявилося, що і його було переписано з іншого, ще давнішого папірусу (третє тисячоліття до н. е.).

Учені розшифрували текст і прочитали кілька задач. Розглянемо одну з них — задачу про поділ хліба.

Старовинна задача. Сто мір хліба треба розділити між п'ятьма робітниками так, щоб другий отримав на стільки само більше хліба за першого, на скільки третій отримав більше за другого, четвертий — за третього, п'ятий — за четвертого. Крім того, двоє перших повинні отримати хліба у 7 разів менше від трьох інших. Скільки мір хліба треба дати кожному?

Щоб розв'язати задачу, спочатку слід ознайомитися з арифметичною прогресією.

План вивчення теми:

1. Означення арифметичної прогресії. Різниця арифметичної про­гресії.
2. Рекурентна формула арифметичної прогресії.
3. Властивості арифметичної прогресії:

1) характеристична властивість арифметичної прогресії;

2) сума членів скінченної арифметичної прогресії, рівновіддалених від її кінців;

3)* теорема про задання арифметичної прогресії формулою a_n = kn + b, де k, b — деякі числа.

Опорний конспект

	Арифметична прогресія — числова послідовність, у якій кожний наступний член, починаючи з другого, дорівнює попе­редньому члену, до якого додається те саме число. Це число називають різницею арифметичної прогресії.
	Приклад. 1; 3; 5; 7; 9 — арифметична прогресія. 3 – 1 = 5 – 3 = 7 – 5 = 9 – 7 = 2; 2 — різниця арифметичної про­гресії.
	Рекурентна формула арифметичної прогресії
	ап+1 = ап + d, d — різниця арифметичної прогресії. d = aп+1 – ап.
Властивості арифметичної прогресії
1.  , де п >1 ап — п-й член арифметичної прогресії, є середнім арифме­тичним двох сусідніх за ним членів.
2.  Якщо (ап) — арифметична прогресія (скінченна), то:
Сума двох членів скінченної арифметичної прогресії, які рівновіддалені від її кінців дорівнює сумі крайніх членів цієї прогресії.
3. Теорема*. Будь-яка арифметична прогресія (ап) може бути задана формулою an = kn + b, де k і b — деякі числа; і на­впаки, якщо послідовність (ап) задана формулою an = kn + b, де k і b — деякі числа, то ця послідовність є арифметичною прогресією.

 

Вивчення матеріалу уроку починається з формулювання озна­чення арифметичної прогресії (учні підготовлені до його сприй­няття на попередньому етапі уроку), у якому слід звернути увагу учнів на словосполучення «починаючи з другого», а також на те, що число, яке додається до кожного члена, починаючи з другого, є сталим для даної арифметичної прогресії, при цьому воно може бути яким завгодно (додатним або від'ємним; цілим або дробовим; воно може дорівнювати навіть 0; це бажано проілюструвати вели­кою кількістю прикладів). Після цього формулюється уявлення про зміст поняття «різниця арифметичної прогресії» та записуєть­ся відповідна формула. Далі традиційно записується рекурентна формула арифметичної прогресії, яка напряму випливає з озна­чення арифметичної прогресії.

Для розв'язування багатьох прикладних задач важливи­ми є властивості арифметичної прогресії, зокрема характерис­тична властивість (хоча програма з математики не дає її серед обов'язкових знань у цій темі). Також не обов'язковою, проте ці­кавою для застосування є теорема про задання арифметичної про­гресії формулою a_n = kn + b, де k, b — деякі числа. Тому, якщо дозволяють особливості класу, можна запропонувати названі влас­тивості арифметичної прогресії розглянути як додатковий матеріал.

V. ЗАСВОЄННЯ НОВИХ ЗНАНЬ І СПОСОБІВ ДІЙ

Для реалізації дидактичної мети уроку слід розв'язати завдан­ня такого змісту:

1. серед запропонованих послідовностей вибрати арифметичні прогресії;
2. указати п-й член та різницю арифметичної прогресії, заданої переліком її перших членів;
3. за рекурентною формулою знайти кілька перших членів ариф­метичної прогресії;
4. вправи на використання властивостей арифметичної прогресії;
5. на повторення: вправи на розв'язування раціональних рівнянь.

Методичний коментар

При розв'язуванні вправ крім закріплення термінології та фор­мул, що виражають властивості, проводиться відпрацювання та­ких ключових моментів: як перевірити, чи є задана послідовність арифметичною прогресією (за означенням, або за характеристич­ною властивістю, або за теоремою, залежно від умови); як знайти різницю арифметичної прогресії (від будь-якого члена, починаючи з другого, відняти попередній до нього член); як знайти член, на­ступний за даним членом арифметичної прогресії (знайти різницю арифметичної прогресії й додати її до даного члену).

 

VI. ЗАСТОСУВАННЯ ЗНАНЬ І ВМІНЬ

1. Робота з підручником
2. Усні вправи

1. Знайдіть четвертий член і різницю арифметичної прогресії:
   1) 2; 7; 12; …;      2) 6; 5,5; 5; …;     3) 0,7; 1; 1,3; …; 4) -9; -7; -5; … .
2. Знайдіть перші чотири члени арифметичної прогресії(а_п), у якої:

1) a₁ = 5, d = 2;    2) a₁ = 7, d = -2.

3. Знайдіть четвертий член арифметичної прогресії:

1) 7; 11; 15; …;    2) 13; 10; 7; … .

4. Знайдіть пропущений член арифметичної прогресії:

1) 1; а₂; 7; а₄; …; 2) a₁; 5; 3; … .

 

3.  Робота в парах

Обговоріть план виконання завдань. Розподіліть, хто виконуватиме завдання варіанту 1, а хто — варіанту 2. Виконайте завдання і здійсніть взаємоперевірку.

Варіант 1	Варіант 2
1) Знайдіть чотири перші члени арифметичної прогресії an, якщо
a1 = 7, d = 3	a1 = 12, d = -5
2) Запишіть наступні три члени арифметичної прогресії:
5,4; 4,8; 4,2;…	2,1; 2,5; 2,9;…
3) Знайдіть третій член арифметичної прогресії an, якщо:
a1 = 4, d = -3	a5 = -9, d = 5

4. Розв’язування задач практичного змісту

1. Повернемося до старовинної задачі і дамо відповідь на запитання «Скільки мір хліба треба дати кожному робітнику?».

Розв'язання

Кількість мір хліба, які одержали робітники, утворюють зростаючу арифметичну прогресію, перший член якої дорівнює х, а різниця – d.

Перший працівник одержить х мір, другий – (х+d) мір, третій – (х+2d) мір, четвертий – (х+3d) мір, п’ятий – (х+4d) мір.

За умовою задачі:

Отже, робітникам треба дати мір хліба.

Відповідь..

2. Курс повітряних ванн починають із 15 хв. у перший день і збільшують час цієї процедури в кожний наступний день на 10 хвилин. Скільки днів слід приймати ванни в зазначеному режимі, щоб досягти їхньої максимальної тривалості 1 година 45 хвилин? 

Дано: арифметична прогресія, а₁=15 хв, d = 10 хв., a_n=105 хв.

Знайти: n

Розв'язання

Відповідь: 10 днів слід приймати ванни. 

3.У період інтенсивного зростання людина росте в середньому на 5 см у рік. Зараз ріст Олексія – 130 см. Якого росту він буде в 2026 році?

Розв’язання

Відповідь:165 см

4.Риболовля

Олег, Петро, Сергій та Андрій ловили рибу. Кількості рибин, які вони впіймали, утворюють арифметичну прогресію. Найменше рибин – 9 – упіймав Петро, а найбільше – 18 – Олег. Скільки рибин упіймали Сергій та Андрій разом? Скільки всього рибин упіймали хлопці?

Розв'язання

В арифметичній прогресії Тому Сергій та Андрій разом зловили 9+18=27 рибин. Хлопці зловили 54 рибини.

5.Про приріст косуль

Раніше поширені скрізь косулі збереглися лише місцями. Їх поголів’я, яке складало більше мільйона особин різко скоротилося: у 1990 році їх залишилося трохи більше 15000. Проте завдяки захисним заходам, прийнятим відносно цього виду в 2005 році їх чисельність досягла 60010 особин. Скільки особин поповнювало ряди косуль в середньому щороку?

Розв'язання

Відповідь:3215 косуль

 

VІI. ПІДБИТТЯ ПІДСУМКІВ УРОКУ, РЕФЛЕКСІЯ

Інтерактивна вправа «Мікрофон».

Учні, передаючи «уявний мікрофон», висловлюються по черзі (слово надається тому, у кого в руках «мікрофон»).

• На сьогоднішньому уроці ми дізналися …

• На сьогоднішньому уроці найважливішим відкриттям для мене було ...

• На початку уроку я поставив перед собою мету. Ось як я її досяг …

• Сьогодні на уроці мені сподобалося …

• Сьогодні на уроці мені було важко …

 

VІIІ. ДОМАШНЄ ЗАВДАННЯ

1. Вивчити означення понять, розглянутих на уроці
2. Розв'язати вправи, аналогічні за змістом та рівнем складності виконаним на уроці.

Повторити схему розв'язування задач складанням математич­ної моделі

Творче завдання для сильних учнів: зобразити графік арифметичної прогресії