Конспект-уроку з алгебри 9 клас та тему: Арифметична прогресія, її властивості. Формула п-го члена арифметичної прогресії.

Про матеріал

Дати означення арифметичної прогресії, ознайомити учнів з формулою п-го члена арифметичної прогресії, навчити знаходити елементи прогресії за формулою n-го члена, визначати зростання і спадання прогресії залежно від d; розвивати обчислювані навички; виховувати любов до історичного минулого.

Перегляд файлу

Тема: Арифметична прогресія, її властивості. Формула п-го члена арифметичної прогресії.

Мета: дати означення арифметичної прогресії, ознайомити учнів з формулою п-го члена арифметичної прогресії, навчити знаходити елементи прогресії за формулою n-го члена, визначати зростання і спадання прогресії залежно від d; розвивати обчислювані навички; виховувати любов до історичного минулого.

Тип уроку: комбінований

Хід уроку.

Організаційний момент.
Перевірка домашнього завдання (усно). Математичний диктант.

Виписати 6 перших членів послідовності, кратних 7.
Парному номеру відповідає число 5, непарному -3. Яке число відповідає ?
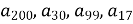Який член слідує за
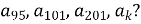
Який член передує члену а₁₇, а₂₆, ?
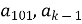Написати невідомі члени послідовності

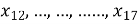Аркуші зібрати для перевірки, а учні беруть зошити.

Ш. Актуалізація опорках знань.

Які є способи задания послідовностей?
Як обчислюються члени послідовності за формулою?
Задайте послідовність словесно і формулою:

а) 1, 2, 3, 5, 8,….;

б) 1, 5, 9, 13,...;

в) 1, 4, 9, 16, 25, ...;

г) 5, 10, 20, 40, ...;

д) 17, 27,37,...;

е) 35, 40, 45, 50, ...;

є) 50, 40, ЗО, 20, ...;

Обчисліть кілька перших членів послідовності за формулою n - го члена:

а) а_n = n / (n + 3);

б) а_n= 2n + 3.

Вивчення нового матеріалу.

Виберіть з усіх послідовностей ті, в яких кожний член, починаючи з другого, знаходили додаванням до попереднього одного й того самого числа. Такі послідовності домовилися називати арифметичними прогресіями,
Означення арифметичної прогресії. ().
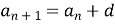Що таке різниця арифметичної прогресії?
Назвати сі у всіх вибраних послідовностях.
Розв’язати №548

Написати сім перших членів арифметичної прогресії, у якої:

а) = 2. d= 5;

б) = 0, d = 1/2;

в) = -3, d = 4;

г) = 4, d = -1;

Які з цих послідовностей є зростаючими, спадними. Від чого це залежить? (Від d).
Вивести формулу n - го члена.

(Учні по черзі записують послідовні члени арифметичної прогресії за їх означенням, поки не побачать закономірність, за якою вони отримані).

Властивість арифметичної прогресії.

Сума двох членів скінченної арифметичної прогресії, рівновіддалених від її кінців, дорівнює сумі крайніх членів.

Чому прогресія називається арифметичною?

(Кожний член арифметичної прогресії дорівнює, середньому арифметичному наступного і попереднього членів, тобто

Історична довідка.

У перекладі з латинської слово прогресія означає рух вперед. Прогресії відомі здавна, а тому не можна сказати хто їх відкрив. Адже натуральний ряд 1, 2, 3, 4,... - це арифметична прогресія, в якій = 1, d = 1.

Задачі на прогресії знайдені на папірусі, що датується 2000 р. до н.е., але і його було переписано з іншого (Єгипет), зустрічаються в одній з найдавніших пам'яток права - “Руській правді”, укладеній ще за Київського князя Ярослава Мудрого (XI ст.)

Значна кількість задач на прогресії є в “Арифметиці” Л. Магницького 1703), що була основним математичним підручником у Росії протягом майже півстоліття.

Тренувальні вправи.

В арифметичній прогресії а₂ =14, 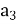= 25. Знайдіть а₁₀, а₂_0/
Знайдіть n - й член арифметичної прогресії:

а) 2, 5, 8, …

б) 7, 6, 5, ...

в) 1/3, 2/3, 1, … .

г) 2, 1,5,1, ....

Скільки від’ємних членів має арифметична прогресія:

а) - 32, -30, -28, ;

б) - 8,5, - 8, - 7,5,

Чи є арифметичною прогресією послідовність, n - й член якої:

а) = 3 n + 1;

б) = 5-4 n;

в) +18.

Знайдіть перший член арифметичної прогресії (а_n), якщо:

а) = 128; d = 4:

б) = - 208; d = -7.

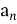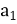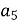Знайдіть різницю арифметичної прогресії (), якщо =10, = 22.
Між числами 5 і 1 вставте сім таких чисел, щоб вони разом із даними числами утворили арифметичну прогресію.