Конспект уроку з алгебри для 8 класу на тему:«Функція у = х² її властивості та графік»

      Тема уроку.  Функція  у = х²   її  властивості та графік

 

Мета  уроку. Домогтися засвоєння  учнями властивостей функції 

                   у = х², виду  і  властивостей її  графіка  та  способу

                   застосування  графіка  функції  у = х²  для  графічного

                   розв’язання  рівнянь  виду х² = а;  формувати  вміння

                   відтворювати  зміст вивчених  понять,  відпрацювати 

                   навички  роботи з  графіком  функції; розвивати 

                   самостійність, уміння  логічно мислити.

Тип уроку. Урок засвоєння  знань  та  вмінь.

 

                                                  Хід уроку

І. Організаційний момент

На цьому етапі уроку слід надати учням інформацію про:

• орієнтовний план вивчення розділу;
• кількість навчальних годин;
• приблизний зміст матеріалу;
• основні вимоги до знань та вмінь учнів;
• приблизний зміст завдань, що будуть винесені на контроль.

Цю інформацію можна розмістити на стенді «Довідково-інформаційний куточок» і запропонувати учням самостійно ознайомитись з нею у позаурочний час.

ІІ. Перевірка домашнього завдання

ІІІ. Формулювання мети й завдань уроку

Поштовхом до вивчення матеріалу уроку може бути завдання, що створює певну проблемну ситуацію:

   «Не розв’язуючи рівняння, доведіть, що рівняння  х² = а (де а – деяке  число) може  мати або два, або один корінь, або не мати жодного кореня, залежно від значення числа а. Дослідіть цю залежність».

 Обговорюючи це завдання учні самостійно, або за допомогою вчителя доходять усвідомлення того, що єдиним на цей момент способом розв’язання задачі є спосіб, який учні опанували під час вивчення попередньої теми. Тобто слід побудувати графіки двох функцій:  у = х²  та  у = а  і  дослідити кількість точок перетину цих графіків залежно від значення  числа  а.

  Таким чином постає питання про необхідність вивчення властивостей функції  у = х²  та  побудову  її  графіка.

ІV. Актуалізація опорних знань

Пригадуємо деякий теоретичний матеріал.

 

Усні вправи:

1. Знайдіть область визначення функції:

   а) ;  б) ;  в) .

2. Функцію  задано  формулою .

   а) Якого значення  набуває функція, якщо аргумент дорівнює 4?

   б) При якому значенні аргументу значення функції  дорівнює ?

3.Чи проходить графік функції    через точки:

   а) А(-1;1);  б) В;  в) С;  г) D?

4. Визначте знак виразу: а) ;  б) ;  в) .

5. Як називається графік функції при ?  Опишіть

    властивості функції.

6. Опишіть вид графіка функції (при ) при ; .

V. Засвоєння знань

План вивчення нового матеріалу

1.Функція у = х² , її область визначення, область значень.

2.Графік функції  у = х², його властивості.

3.Приклади задач на застосування  властивостей функції  у = х².

VІ. Формування вмінь

Усні вправи:

1. Які з точок не належать графіку  функції  у = х² :   (-1;1);  (-2;-4);  (0;8);  (3;-9); (1,7; 2,89);  (16; 0)?

2.Скільки спільних точок можуть мати пряма і графік функції у = х²?

3. а) Піднесіть до другого степеня:  ;

    б) Назвіть числа, квадрати яких дорівнюють: .

Виконання письмових вправ.

Для досягнення мети уроку мають бути розв’язані вправи такого змісту:

1.Знаходження значень функції  у = х² (аргументу), що відповідають 

   даним значенням аргументу (функції) за формулою.

   Виконати № 350 за підручником (А.Г.Мерзляк.  Алгебра  8 клас).

2.Знаходження за готовим графіком функції  у = х²  значень  функції

   (аргументу), що відповідають даним значенням аргументу (функції).

      Користуючись графіком функції  у = х² ,  знайдіть  значення

    аргументу, яким відповідають такі значення функції: 1,5;  3,5;  7,5.

    Виконати № 357  за підручником.

3. Визначення, чи належить задана точка графіку функції  у = х².

       Чи проходить графік функції  у = х²  через  точки: 

        ?

4. Побудова графіка функції  у = х²  разом із графіком якої-небудь

    функції  та знаходження координат спільних точок цих графіків

    (точок перетину).

    Виконати № 355(1, 4) за підручником.

5. Графічне розв’язування рівнянь.

    Виконати № 353(2) за підручником.

6. Логічні вправи та завдання підвищеного рівня складності для учнів,

    які мають достатній та високий рівні знань.

       1) Знайдіть значення b, при якому графіки функцій і

           у = х² мають лише одну спільну точку. Які координати цієї

           точки.

       2) Користуючись графіком функції у = х², укажіть значення х,  при

           яких  точки параболи розміщені нижче від прямої .

VІІ. Підсумок  уроку

В якому з випадків правильно вказано значення параметра а?

а) а = –2                                    б) а = 2                                 в) а = 4

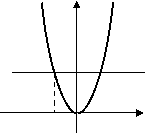
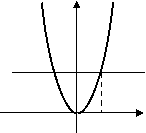
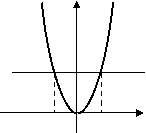                  у                                        у                                           у

                         у = х²                                 у = х²                                   у = х²

 

у = а                               у = а                                      у = а

 

 

         -2     0            х                      0      2        х                     -2  0     2        х

VІІІ. Домашнє завдання

1. Вивчити властивості функції  у = х² , схему побудови  її графіка.

2. Виконати   № 354(1);  №356(1)  за  підручником (А.Г.Мерзляк. 

    Алгебра  8 клас).