Конспект уроку з геометрії 8 клас на тему " Розв*язування вправ" ( теорема Піфагора)

Несватківська філія КЗ « Олександрівське НВО № 2»

 

 

 

 

конспект уроку геометрії

у 8 класі

 

на тему:

 

 

( Теорема Піфагора. Перпендикуляр і похила)

 

 

 

 

 

 

 

Підготувала і провела

Коломієць  В. О.

 

 

 

 

 

 

 

2019 р.

 

Тема: Розв'язування вправ

Мета:повторити з учнями зміст теореми Піфагора та наслідків з неї; формувати вміння застосування  теореми при розв’язуванні задач. Розвивати логічне мислення, пізнавальну активність учнів,обчислювальні навички, увагу, кмітливість, формувати навички самооцінки, виховувати інтерес до  математики. розуміння ролі геометрії у вирішенні практичних завдань

Тип уроку:комбінований

Обладнання: конспект, підручник, портрет Піфагора, картки для практичних робіт.

Хід уроку

І. Організаційний момент.

Світ, що нас оточує, - це світ геометрії. Нехай  сьогоднішній урок стане ще одним віконцем у дивовижний і цікавий математичний простір.

ІІ Перевірка домашнього завдання

Фронтальне опитування

ІІІ. Повідомлення теми, мети уроку, мотивація навчальної діяльності.

Найпопулярнішою з усіх теорем планіметрії є теорема Піфагора. Причинами такої популярності є простота, краса і значення.

В будь-якій задачі, де ми стикаємося з прямокутним трикутником завжди є місце для теореми Піфагора. А прямокутний трикутник зустрічається і в квадраті, і в прямокутнику, ромбі, трапеції, в колі і в багатьох інших фігурах.

Тому метою нашого уроку буде:  повторення знань про властивості прямокутного трикутника; застосовування набутих знань, умінь і навичок до розв’язування задач які містять прямокутний трикутник, безпосередньо застосовування теореми Піфагора для знаходження відстаней між точками.

ІV. Актуалізація опорних знань та умінь.

Бліц-опитування

1. Як називаються сторони прямокутного трикутника, які утворюють гострий кут?

(катет і гіпотенуза )

2. Сторони прямокутника 8 см і 15 см. Знайдіть його діагональ. (17 см)

3. Як читається теорема Піфагора?

  (квадрат гіпотенузи прямокутного трикутника дорівнює сумі квадратів його  катетів)

4. Катети прямокутного трикутника дорівнюють 5 і 12 см. Чому дорівнює гіпотенуза трикутника?       (13 см  )         

5. Гіпотенуза прямокутного трикутника дорівнює 10 см, а один з катетів 8 см. Чому дорівнює другий катет?              (6 см )          

6. Порівняйте катети а і в прямокутного трикутника з його гіпотенузою с.

 (a<c, в <c)

7. Чи буде прямокутним трикутник зі сторонами 9 см, 12 см і 15 см. (ні  )         

8. Відрізок, що з’єднує основу перпендикуляра з основою похилої, проведеної з тієї ж точки, називається ( проекцією)
9. Рівні похилі мають рівні (проекції)

V. Формування вмінь

1)Робота з підручником колективно

№ 432. №446

 

Вправи для зняття втоми очей.

1.Заплющити очі. Не відкриваючи очей, начебто подивитися ліворуч на рахунок „раз-чотири”, повернутися у вихідне положення. Так само подивитися праворуч на рахунок „п’ять-вісім” і повернутися у вихідне положення. Повторити 5 разів.

2.Спокійно посидіти із закритими очима, розслабившись протягом 5 с.

2)Робота з індивідуальними картками

 Опорна  картка –підказка (один слабкий учень)

1  Серед даних трикутників вказати прямокутний

 

 

 

 

 

 

 

 

 

2 Яку назву мають сторони що утворюють прямий кут?

 

 

 

 

 

 

3 Як  називається найбільша сторона прямокутного трикутника?

 

 

 

 

 

 

4 Теорема Піфагора формулюється так: Квадрат гіпотенузи дорівнює сумі....

5 Задача

Знайти гіпотенузу прямокутного трикутника якщо катети дорівнюють 6 см та 8 см

 

АВ²=АС²+СВ²

АВ= АС²+СВ² =

 

1 Діагональ прямокутника дорівнює 10см, а одна з його сторін 8 см. Знайдіть периметр прямокутника.

Картка-підказка для учня(один учень)

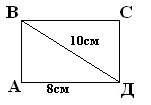1)Розглянути трикутник   АВД (кут А=90°  АД=8 см  ВД= 10 см

2. Знайти АВ застосувавши теорему Піфагора

ВД²= АВ²+ АД²

АВ²⁼

АВ=

3) Що таке периметр?

4)Як обчислити периметр прямокутника?

                                           Р=2АД+

5)Р=2•8+2• АВ=

Відповідь:

Картка для роботи в парі

1 Діагональ прямокутника дорівнює 10см, а одна з його сторін 8 см. Знайдіть периметр прямокутника

2. У прямокутній трапеції АВСД з основами АД і ВС, кут А прямий, АВ = 4 дм. з вершини С до основи АД проведений перпендикуляр СК, КД= 3дм,  Знайдіть СД.

 

Дано: АВСД – прямокутник, ВД -  діагональ, ВД = 10 см,                                        АД=8 см.

Знайти: Р

Розв’язання:

          Р=(АВ +ВС)× 2

 Трикутник АВД - прямокутний, за теоремою Піфагора

    АВ=

АВ=

Р=(6+8)× 2 = 28(см)

 

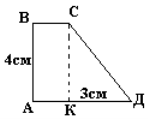
Дано: АВСД – трапеція, <А = АВ=4 дм.

СК АД  КД=3 Знайти: СД

         Розв’язання

 Оскільки АВСД трапеція АД//ВС

 АВ//СК, АВ=СК=4 дм; Розглянемо

  По теоремою Піфагора    СД²=КД² + СК²;

(дм.)

 Відповідь 5дм.

 

Задача . ( для  пожежників) практичне застосування  теореми Піфагора

  Якої  довжини  має  бути  драбина, щоб  її  можна  було б   приставити  до  вікна,  що  знаходиться  на  висоті  6 м  від  землі,  коли  відстань  від  нижнього  кінця   драбини  до  будинку   повинна  дорівнювати  2,5 см?

 

Розв’язання.

Так  як  стіна    перпендикулярна  до  землі  драбина  і  стіна  утворять         прямокутний

                            За  т. Піфагора 

              АВ = =   = = = 6,5 ( м)

Відповідь: 6,5 м.

 

 

VІІ. Підсумки уроку.

«Корисні та шкідливі звички».

• Які риси характеру допомагали вам досягти успіху на уроці?
• Які заважали?                                                                                                              

активність	пасивність	ввічливість	Упертість
дисциплінованість	допитливість	ініціативність	Наполегливість
неуважність	незібраність	недбалість	працелюбство
організованість	лінь	уважність	відповідальність

 

VІІІ. Домашнє завдання:

Повторити §13

Скласти задачу практичного змісту для розв'язування якої необхідне застосування теореми Піфагора