Конспект уроку з геометрії для 7 класу на тему: «Вертикальні кути та їх властивості»

Урок  з геометрії, 7 клас

Автор: Чернишева О.В.

Навчальний заклад : Дружківська ЗШ І-ІІІ ступенів №7

Вертикальні кути та їх властивості

Мета:  1) надати визначення вертикальних кутів, сформувати вміння будувати вертикальні кути, знаходити вертикальні кути на рисунку, розв’язувати задачі із застосуванням теореми про рівність вертикальних кутів та суму суміжних кутів;

 розширити знання учнів про культуру українського народу, формувати національну свідомість, любов до рідної землі, свого народу, держави, народу;

        2) розвивати логічне мислення учнів, формувати вміння аналізувати; дбайливе ставлення до національних багатств, шанобливе ставлення до національних та державних символів;

               3) виховувати культуру оформлення геометричних задач,  інтерес до предмету, охайність записів, культуру математичної мови.

 

Тип уроку: урок засвоєння навичок та вмінь.

Структура уроку

I. Перевірка домашнього завдання

II. Повідомлення теми, мети і завдань уроку і мотивація навчання школярів.

III. Актуалізація опорних знань.

IV. Вивчення нового матеріалу (ввідні вправи).

V. Застосування набутих знань (пробні вправи).

VI. Творче застосування знань і навичок у нових умовах з метою формування вмінь (творчі вправи).

VII. Підсумки уроку і повідомлення домашнього завдання.

Хід уроку

   І. Перевірка домашнього завдання.

   Вчитель повідомляє учням про те, що в кінці уроку вони мають здати зошити з домашнім завданням на перевірку.

 

II. Повідомлення теми, мети і завдань уроку і мотивація навчання школярів.  

   Сьогодні ми з вами, як ви вже зрозуміли, дізнаємося,  які кути називаються вертикальними. Ви мабуть всі знаєте значення слова «вертикально». «Вертикальний» - це «стрімкий, що йде згори донизу». Яким же чином можна говорити, що кути вертикальні? Справа тут ось в чому. Латинське слово verticals - утворено від слова vertex - вершина. Тому термін «вертикальний» має два значення «стрімкий» і «вершинний». Коли говорять про кути, то мають на увазі друге значення. Отже, щоб не плутати ці два поняття давайте дізнаємося, що ж таке вертикальні кути?

III. Актуалізація опорних знань.

1. Які кути називаються суміжними?

2. Чи можуть бути суміжними три кути?

3. Чому дорівнює сума суміжних кутів?

4. Знайдіть кут, суміжний з кутом 30°; 90°; 120°(усно).

5. Дано кут. Один з кутів, суміжний з даним кутом, дорівнює 50°. Чому дорівнює інший кут, суміжний з даним?

-Знайдіть суміжні кути на гербі нашого міста та в назві ДРУЖКІВКА

 

 

 

 

 

 

 

 

 

 

IV. Вивчення нового матеріалу (ввідні вправи).

   Побудуйте кут АОB.(учні в зошитах, вчитель на дошці)

   Проведіть доповняльні промені до його сторін.(учень на дошці)

   Дістанемо два кути АОB і СОD зі спільною вершиною О. Такі кути є вертикальними.

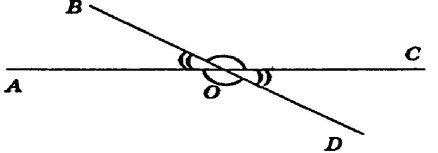
   Давайте спробуємо разом сформулювати означення вертикальних кутів, виходячи зі способу іх побудови.(Учні з допомогою вчителя формулюють означення вертикальних кутів.)

   Означення. Два кути називають вертикальними, якщо сторони одного є доповняльними променями сторін іншого.

   Запитання до дітей: -Чи можуть три кути бути вертикальними?

-Який предмет побуту надає нам уявлення про вертикальні кути?

-Скільки пар вертикальних кутів утворюється при перетинанні двох прямих 

 

   Вчитель: Намалюємо вертикальні кути та за допомогою транспортиру виміряємо їх градусні міри.  Що ми бачимо?  

  - Цікаво, а чи завжди так буде чи тільки в даному випадку?

   Розв’яжемо задачу. Кут 1 і кут 2 вертикальні. Кут 3 дорівнює 120 градусів. Знайти кути 1 і 2.

- А якщо ми візьмемо загальний випадок, чи отримаємо ми такий же результат?

Вчитель формулює і доводить разом з учнями (використовуючи розв’язок попередньої задачи) теорему про вертикальні кути .

   Теорема. Вертикальні кути рівні. 

    А К D 

 

Доведення.  Нехай  AKC      і  DKB   вертикальні  кути  (рис.  59). Тоді якими є кути AKC і  AKD?

Учні: суміжними,

Вчитель: Їх сума дорівнює…

Учні:  AKC  + AKD  =  180°.

Вчитель: А кути  AKD  і   DKB –

Учні: теж суміжні, тому AKD  + DKB = 180°.

Вчитель: Маємо: AKC  = 180° – АКD   і  DKB = 180° – AKD .

 Праві частини цих рівностей рівні, тоді який можемо зробити висновок?

Учні: тому рівними є й ліві частини. Отже, AKC  = DKB.

Теорему доведено.

   Запитання для учнів: Якщо  1  і  2 вертикальні і 1= 47°, то чому буде дорівнювати 2?

   V. Застосування набутих знань (пробні вправи).

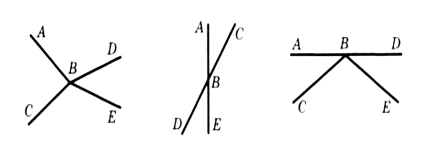
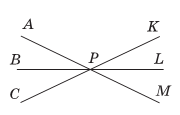
   Задача 1. Чи є вертикальними кути зображені на малюнку. Назвіть всі пари вертикальних кутів (рис. 1).

1. 2                             3                                     4

Учні:

1. Оскільки сторони одного кути не є доповняльними променями сторін іншого, кути не вертикальні оскільки.

2. За означенням вертикальних кутів, кути  ABC i DBE, а також ABD i  CBE є вертикальними.

3. Оскільки СB не є доповняльним променем до BE, то кути не вертикальні.

4. За означенням вертикальних кутів, кути  APB і LPM , а також KPL і   BPC, APC і KPM є вертикальними.

   Коментована вправа: учні детально пояснюють свої міркування, кожен раз формулюючи означення,  дають відповідь.

   Задача 2. Один з кутів, що утворилися при перетині двох прямих, дорівнює 40°. Знайдіть інші кути (рис. 2).

Рис. 2

Розв’язання

1) Нехай   2 = 40°, тоді кут  4= 40, як вертикальний до  2.

2) 1+2=180°, оскільки 2 і  1 – суміжні. Отже, 1=180°- 2=180-40=140°

3) 3 =1=140°, оскільки  1 і  3 – вертикальні.

Відповідь:  1= 3=140°, 2= 4= 40°.

   Учні виконують завдання біля дошки пояснюючи свої дії, можна вже не вимагати повторення означень.

   Задача 3. Сума двох вертикальних кутів дорівнює 120°. Знайти значення кожного з кутів.

Розв’язання

1)   Сума двох вертикальних кутів дорівнює 120°, отже 1+2=120°.

2) 1= 2 , за теоремою про вертикальні кути, тому 1+1= 2*1=120°.

2) 1= 2= 60°.

Відповідь:  1= 2= 60°.

   Учні виконують дану задачу самостійно у парах і говорять відповідь.

   VI. Творче застосування знань і навичок у нових умовах з метою формування вмінь (творчі вправи).

Вчитель:  А зараз перевіримо, чи все вам зрозуміло з даної теми для цього дайте відповіді на запитання, а потім виконайте творче завдання.

  Запитання (дати відповідь так чи ні):

1. Якщо кути рівні, то вони вертикальні. 

2. Якщо два кути мають спільну вершину, то вони вертикальні.

3. Два прямі кути можуть бути вертикальними.

Творче завдання. Вертикальні кути мі можемо побачити всюди навколо нас. Сьогодні ми будемо шукати їх у візерунках українських вишиванок.

 

Вишивка - класичний вид українського народного мистецтва, що розкриває невичерпне багатство творчих сил народу, вершини його мистецького хисту.

У процесі історичного та культурного розвитку на Україні у кожній місцевості утворились характерні орнаментальні мотиви і композиції, найбільш улюблена і поширена колірна гама, специфічні техніки виконання. Дбайливо передавалися вони з покоління в покоління, майстри відшліфовували кращі досягнення своїх попередників, розвиваючи і вдосконалюючи їх. Вишивкою займалися повсюди. Кожний район, навіть кожне село відзначалися своєрідністю мотивів. Ось тому вишивка - це не

тільки художнє оформлення речей, а й своєрідне світобачення відтворене специфічними художніми засобами. В українській вишивці органічно співіснують рослинний і геометричний орнаменти. Геометричні мотивистали основою східнослов'янського узору.

Отже, починаемо (робота у парах, учні позначають вертикальні кути на картках з візерунками)

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

VII. Підсумки уроку і повідомлення домашнього завдання.

   Підведіть свої результати на уроці, заповніть лист самооцінки, враховуючи всі види робіт і вашу участь в них. Поставте свою оцінку:

  Я все зрозумів правильно. Для мене всі завдання були зрозумілі.

Більша частина моїх відповідей правильна, на деякі питання я дав неправильні відповіді, мені потрібно ще попрацювати над цією темою.

 У мене дуже багато помилок, напевно, я неуважно слухав пояснення вчителя і працював не на повну силу; потрібно добре попрацювати вдома.

   Домашнє завдання:

1. Знайдіть усі кути, що утворилися в результаті перетину двох прямих, якщо:
а) сума двох із них дорівнює 320°;

б) один із цих кутів на 50° менший за інший.

2. Знайдіть кут між двома прямими, які перетинаються, якщо:

а) сума двох утворених кутів на 80° менша, ніж сума двох інших кутів;

б) один із кутів, що утворилися, удвічі менший за суму решти трьох кутів.

3. У результаті перетину двох прямих утворилися чотири кути, один із яких є прямим. Доведіть, що решта кутів також прямі