Урок-проект з геометрії «Трикутник»

Група «Історики»

Наша група досліджувала історію розвитку вчення про трикутник та трикутник як символ. Опрацювавши інформаційний матеріал, інтернет-ресурси, ми встановили, що вчення про трикутник розвивалося в Стародавній Греції у іонійській школі, школі Піфагора, у Стародавньому Китаї, Стародавньому Єгипті, в арабських країнах, Вавилоні, Стародавній Індії.

Задачі про трикутник були знайдені у давньогрецьких папірусах, старовинних індійських книгах. У папірусі Ахмеда згадується про рівнобедрений прямокутний трикутник, давні Вавилоняни 4 тис. років тому уже знали про властивість кутів при основі рівнобедреного трикутника.

Вважається, що Фалес Мілетський першим познайомив греків з геометрією. Він же довів теорему про рівність кутів при основі рівнобедреного трикутника. Саме Фалесу приписують доведення другої ознаки рівності трикутників, так як він використовував її для визначення відстані від берега до морських кораблів.

Землеміри Стародавнього Єгипту для побудови прямого кута ділили мотузку вузлами на 12 рівних частин і кінці зав’язували. Потім мотузку розтягували по землі так, щоб утворився трикутник зі сторонами 3, 4 і 5 вузлів. Кут, що лежав проти сторони в 5 вузлів – прямий.

Піфагору та його учням належать вчення про прямокутний трикутник.

У першій книзі «Начал» Евкліда описуються властивості трикутників. Серед визначень є такі: «З тристоронніх фігур рівносторонній трикутник є фігура, яка має три рівні боки, рівнобедрений – має тільки дві рівні сторони, різнобічний має три нерівні сторони». У 15-16 століттях з’явилась величезна кількість досліджень властивостей трикутника, які увійшли в розділ планіметрії під назвою «Нова геометрія трикутника».

Трикутник – один із найпотужніших і універсальних символів. Рівносторонній трикутник вершиною вгору – чоловічий сонячний знак, який представляє божество, вогонь, життя, благополуччя, гармонію і королівську владу. Трикутник вершиною вниз – символ, пов’язаний з місяцем, представляє воду, холод, природу, жіночу основу, символізує велику матір. Трикутники, що перетинаються, утворюючи гексакграму, символізують синтез, союз протилежностей, а також символ людської душі.

В індуїзмі і християнстві трикутник – знак Бога. Бог християнської Трійці інколи представлений оком всередині трикутника. Трикутник є поширеним символом на писанках, килимах, рушниках, посуді. Він є основою, нижнім ярусом стилізованого дерева життя.

Працюючи над проектом, ми дійшли до розуміння того, що дуже багатьох вчених цікавив трикутник, так як практично скрізь ми зустрічаємо цю геометричну фігуру: в архітектурі, економіці, мистецтві, психології.

 

 

 

 

 

 

 

 

 

 

 

 

Група «Дослідники»

Наша задача – дослідити розміщення висот, медіан та бісектрис в трикутниках та довести, що трикутники живуть не лише на сторінках підручника геометрії. Результатом нашого дослідження є презентація.

Якщо в трикутнику провести всі три бісектриси, то вони перетнуться в одній точці, яка знаходитиметься у внутрішній частині трикутника. Ця визначна точка трикутника буде центром вписаного в трикутник кола, на що ми просимо звернути увагу. А так як ми група дослідників, то до вашої уваги малюнки, де ми шукали центр вписаного кола для різних видів трикутників.

Якщо в трикутнику провести три медіани, вони перетнуться в одній точці, яка належить трикутнику, при чому, в цій точці вони діляться на відрізки у відношенні 2:1, починаючи з вершини. Ця визначна точка трикутника називається центроїдом. На цьому дослідженні бачимо (малюнок) 15:7.5=2:1 і 12:6=2:1. Отже, на нашому слайді всі відношення AO:OM=BO:ON=CO:OP=2:1.

Якщо провести три висоти трикутника, вони теж перетнуться в одній точці, але для прямокутного трикутника ця визначна точка буде вершиною С з прямим кутом. У тупокутному трикутнику знаходитиметься за межами трикутника, у гострокутному у внутрішній області. Точку перетину висот називають ортоцентром.

Якщо ви нас уважно слухали, то зможете пояснити, чому на наших малюнках ми проводили по дві бісектриси, по дві медіани? (Так як третя бісектриса, медіана або висота пройде через точку перетину інших). Це обов’язково необхідно пам’ятати при розв’язуванні задач

У рівносторонньому трикутнику висота, медіана і бісектриса, проведені з однієї точки, збігаються, а значить точка перетину висот, медіан і бісектрис одна.

Дуже цікавим для нас було дослідження трикутника Наполеона, який полюбляв геометрію, і залишив для нащадків декілька задач. Так от, якщо на кожній стороні довільного трикутник АВС побудувати по рівносторонньому трикутнику, а потім знайти точку перетину їх бісектрис (можна медіан, висот, адже ми знаємо, що вони збігаються в рівносторонньому трикутнику), то трикутник з вершинами в точках О₁, О₂, О₃ обов’язково рівносторонній. Проробивши не одну таку побудову ми впевнилися, що це завжди так.

Дивне було відкриття, зроблене американським математиком Ф.Морлі. Якщо в трикутнику провести промені, що ділять кути на три рівні частини (трисектриси), то точки перетину суміжних трисектрис є вершинами рівностороннього трикутника.

З усіх многокутників тільки трикутник – фігура жорстка. Це ми можемо продемонструвати на моделі. А тому ажурні конструкції опор, мостів виготовляють так, щоб вони мали якомога більше трикутників, що ви можете побачити на слайді.

Як виявилося, трикутники дуже різноманітні, досліджували їх багато різних людей, і робили все це з метою практичного їх застосування, як в математиці, так і в житті. І ми впевнені, що трикутник зберігає ще якісь таємниці, які зможемо розкрити ми.

 

 

 

 

 

 

 

 

Група «Практики»

Наша задача – опрацювати збірник задач, інтернет-ресурси, підручник, підібрати задачі, продумати їх розв’язання та відповідно оформити, а також підібрати задачі для їх самостійного розв’язування. Для уроку ми пропонуємо слідуючі задачі:

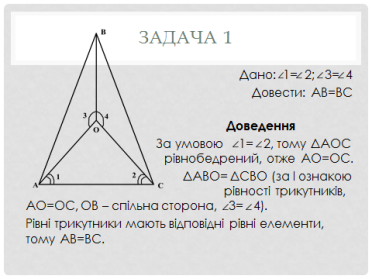
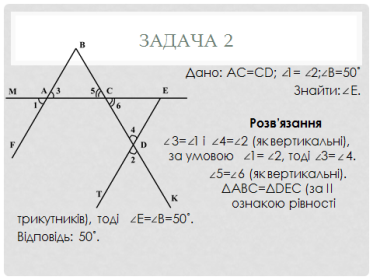
Ми знайшли цікаву презентацію, яка називається «Задачі за готовими малюнками» і, якщо ви їх опрацюєте, то отримаєте тільки відмінні оцінки.

Ми не повинні бути байдужими до геометрії, а полюбити цей красивий предмет. А щоб розвинути інтуїцію, набути досвіду геометричного зору, необхідно більше розв’язувати задач і тоді ми будемо готові і до здачі ДПА та ЗНО і до навчання в майбутньому.

 

 

 

 

 

 

 

 

 

 

Група «Пошуковці»

Опрацювавши різний інформаційний матеріал, інтернет-ресурси, ми не очікували такої популярності трикутників.

 Бермудський трикутник – район в Атлантичному океані, в якому відбуваються таємничі зникнення морських і повітряних суден. Американський дослідник Лоуренс Куш провів ціле дослідження і з’ясував, що майже 90% всіх містичних випадків в цьому районі або вигадані, або мають раціональне пояснення. «Легенда про Бермудський трикутник – це сфабрикована містифікація», - прийшов до висновку Лоуренс Куш. «Вона виникла в результаті недбало проведених розслідувань». Аналогічний трикутник в Тихому океані називається Диявольським.

        Драматичний трикутник або трикутник Карпмана. Три драматичні ролі є насправді мелодраматичним спрощенням реального життя. Ми бачимо себе щедрими рятівниками, вдячними чи невдячними жертвами, праведними переслідувачами нечестивих, лінивих. Занурюючись в будь-яку з цих ролей, ми починаємо ігнорувати реальність як актори на сцені, щоб створити хороший спектакль. При цьому ми ніколи надовго не затримуємо в одній ролі. Наприклад,учень 7 класу-жертва,що переслідується  однокласниками,які провокують на прогули та порушення поведінки, а класний керівник –рятівник.

       Відомим є правило «золотого трикутника», яке використовують у торгівлі. Знайшовши в магазині потрібний товар, покупець іде до каси. Завдання продавця розташувати товар, що користується найбільшим попитом у вершинах уявного трикутника саме для того, щоб змусити покупця пройти весь периметр магазину. Чим більша площа трикутника між входом, касовим вузлом і товаром, тим більш вдалим можна назвати планування магазину, від чого залежить об’єм продажу товарів.

Трикутник Паскаля – математичне поняття , назване на честь Блеза Паскаля – французького математика, фізика, філософа. Його легко запам’ятати, так як ряди пронумеровані згори та починаються з одиниць. На бічних сторонах теж стоять одиниці. А числа всередині одержуємо, додавши два числа, розміщені вгорі (зліва та справа). Якщо подивимось на третій ряд, це записані коефіцієнти квадрата двочлена, формулу, яку ми вже зустріли в алгебрі.

Серед неможливих фігур є трикутник Пенроуза (трибар), як один із яскравих математичних парадоксів. Дивлячись на нього, неможливо не повірити в його реальне існування. Але це ілюзія, яку може пояснити лише геометрія. Зображений у 1938 році шведським художником у вигляді набору кубиків трибар став відомим завдяки англійському математику Роджеру Пенроузу, який зобразив його у вигляді трьох балок з’єднаних під прямими кутами. Але ж ми знаємо, що це неможливо.

Наш великий світ складається з дрібних частинок. І якщо якась маленька деталь зникне, зламається весь механізм, який будувався тисячоліттями. На жаль,  ми часто не звертаємо уваги на дрібниці так само, як і не помічаємо того, що завжди оточує нас. Працюючи над проектом, ми дійшли висновку, що практично скрізь присутня геометрична фігура – трикутник, а значить, з трикутником пов’язана не лише математика, а й наше повсякденне життя.