Конспект уроку з геометрії для 8 класу з теми "Середня лінія трапеції"

Конспект уроку з геометрії

для 8 класу

з теми "Середня лінія трапеції"

Задачі уроку:

• Закріпити навички розв’язування задач;
• Навчати розв’язувати задачі різними способами;
• Перевірити степінь засвоювання матеріалу;
• Розвивати логічне мислення, математичну пам'ять, мову;
• Виховувати інтерес до предмету;
• Сприяти вихованню в учнів точності, охайності.

Обладнання:

• Малюнки для усного рішення задач.

Хід уроку:

1. Фронтальне повторення:

1. Активізація класу;
2. Перевірка домашнього завдання;
3. Усне рішення задач.

2. Рішення задач.

4. Задачі на середню лінію трапеції.

3. Домашнє завдання.
4. Підсумок уроку

І. Фронтальне повторення:

1. Перевірити готовність учнів до уроку, активізувати увагу.

2. Перевірити домашнє завдання. №331 (3); №334; №337 розв’язують троє учнів біля дошки.

3. На дошці зображені малюнки до вправ і задач для усного рішення.

Задача 1 спрямована на тренування «геометричний зір».

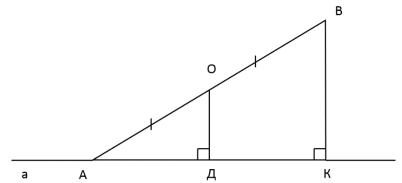
1. Чим є ВК на малюнку?

Відповідь. Відстань від кінця відрізка АВ до прямої а, катет прямокутного трикутника АВК, перпендикуляр до прямої а, основа прямокутної трапеції.

2. Чим є ОД на малюнку?

Відповідь. Середня лінія трикутника АВК (за теоремою Фалеса), відстань від середини відрізка АВ до прямої а, перпендикуляр до прямої а, катет трикутника АОД, менша основа прямокутної трапеції, відрізок від однієї з двох паралельним прямих.

3. Знайти ОД, якщо ВК дорівнює 20 см.

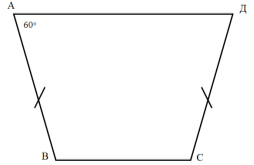
Задача 2. Знайти середню лінію трапеції АВСД.

Дано: АВ = 10 см, АД = 30 см, кут А = 60°

Учні знаходять чотири способи рішення.

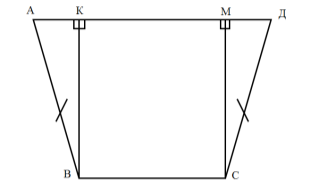
1 спосіб.

Проведемо ВК перпендикулярно АД і СМ перпендикулярно АД.

З трикутника АВК, де кут АВК = 30°, знайдемо АК.

АК = ½ АВ = 5 см.

ВС = КМ = АД – 2 АК = 30-10 = 20 см.

Середня лінія: (30+20) / 2 = 25 см

2 спосіб.

Побудуємо ВО паралельно СД, тоді кут ВОА = куту СДО = 60° (кути із сонаправленими сторонами). Трикутник АВО – рівносторонній, тоді

АО = 10 см, ОД = 30 – 10 = 20см, ВС = ОД = 20см, оскільки ВСДО – паралелограм. Середня лінія 25 см.

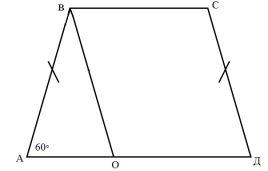
3 спосіб.

Нехай ВО бісектриса кута АВС (згідно з тим самим малюнком), тоді трикутник АВО – рівносторонній, тоді АО = 10 см, ОД = 30 – 10 = 20см, ВС = ОД = 20см, оскільки ВСДО – паралелограм. Середня лінія 25 см.

4 спосіб.

Продовжимо АВ і ДС до перетину в точці М. Трикутник АМД – рівносторонній, ВМ = 30 – 10 = 20см, трикутник ВМС – рівносторонній (кут МВС = куту ВАД = 60°). ВС = 20см. Середня лінія 25 см.

ІІ Рішення задач.

Учні працюють в групах.

Перша група одержує задачі на картках. Учні розв’язують задачі в зошитах, рішення перевіряється на дошці.

Задача 1. Діагональ рівнобічної трапеції ділить її середню лінію на відрізки довжиною 5 см і 11 см, бічна сторона 12 см. Знайти кути трапеції.

Задача 2. Дана трапеція АВСД, АД і ВС основи. З кута В проведено бісектрису, яка перетинає середню лінію трапеції в точці О, а основу АД – в точці Р. Знайти кут АОР.

Друга група.

Задача 1. В прямокутній трапеції менша основа 3 см, менша бічна сторона 8 см, тупий кут 135°. Знайти середню лінію трапеції.

Задача 2. В рівнобічної трапеції діагональ є бісектрисою гострого кута, одно з основ на 6 см більша за другу. Знайти середню лінію трапеції якщо периметр дорівнює 74 см.

Всі задачі перевіряються на дошці і індивідуально у кожного з тих учнів, які розв’яжуть їх протягом уроку.

ІІІ. Домашнє завдання.

IV. Підсумок уроку.