Конспект уроку з геометрії "Теорема Фалеса". 8 кл
Урок ГЕОМЕТРІЇ. 8 клас
Тема: ТЕОРЕМА ФАЛЕСА
Мета:
Навчальна: формувати в учнів усвідомлене розуміння змісту теореми Фалеса та способу її доведення; вміння відтворювати формулювання теореми Фалеса, застосовувати її для розв'язування задач на знаходження довжин відрізків, що відтинаються на сторонах паралельними прямими, розв'язувати задачі на поділ відрізка на n рівні відрізки або в даному відношенні.
Розвивальна: розвивати пам’ять, розумову активність, логічне мислення; формувати науковий світогляд, розуміння важливості свідомого й міцного володіння системою математичних знань, навичок і умінь, необхідних у повсякденному житті, майбутній трудовій діяльності, достатніх для вивчення інших дисциплін та продовження освіти.
Виховна: виховувати інтерес до математики та історії, уважність, акуратність, дисциплінованість.
Обладнання: ноутбук, мультимедійний проектор, відеофільм «Фалес Мілетський. Історія одного вченого», презентація уроку, косинець, лінійка, циркуль, картки із завданнями, підручник «Геометрія 8 клас» (авт. О.С.Істер, 2016 р.в.)
Тип уроку: урок вивчення й первинного закріплення нових знань
ХІД УРОКУ
- Організація початку уроку (2.5 хв)
1. Діти записують у зошити: дата, класна робота.
2. Ознайомлення з думкою угорського математика Д. Пойа: «Потрібно всіма засобами навчати мистецтву доведення, не забуваючи при цьому про мистецтво здогадуватися».
3. Настанови щодо ефективного проведення уроку.
Виконання усних вправ за готовими рисунками (2.5 хв)
|
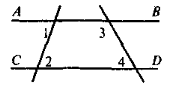
1 |
|
Дано:
Довести: |
|
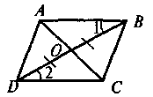
2 |
|
Дано: ВО = ОD, |
|
3
|
|
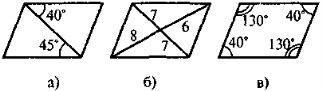
Які помилки допущено в зображенні паралелограма |
- Мотивація навчальної діяльності (5 хв)
Сьогодні ми познайомимося з видатним ученим Давньої Греції та його математичним винаходом.
«Як ви думаєте, чи можуть знання відкрити шлях до багатства?»
Пропоную переглянути відеофільм і дати відповідь на моє запитання.
Перегляд фільму «Фалес Мілетський. Історія одного вченого»
Питання до класу після перегляду фільму: «Чи згодні ви, що один зі шляхів до збагачення – це знання?»
Тож учімося, щоб жити гідно як Фалес!
- Повідомлення теми та мети уроку
Тема нашого уроку «Теорема Фалеса».
Давайте разом сформулюємо мету уроку! (Вивчити теорему Фалеса, навчитися її застосовувати при розв’язанні задач, зрозуміти, як можна її використати в житті)
(Дата, Класна робота, тема і мета уроку записується на дошці та в зошиті)
- Підготовка учнів до засвоєння, актуалізація опорних знань. Інтерактивна вправа «Незавершене речення» (5 хв)
- Прямі, що не перетинаються, називаються … (паралельні).
- Перша ознака рівності трикутників за … (двома сторонами і кутом між ними)
- Друга ознака рівності трикутників за … (стороною і прилеглими кутами)
- Медіана трикутника сполучає його вершину із (серединою протилежної сторони)
- Паралелограм – це чотирикутник, у якого …(протилежні сторони попарно паралельні)
- Протилежні сторони паралелограма … (рівні)

- Вивчення нового матеріалу (10 хв)
Завдання. Щоб розрізати дошку на 5 рівних частин (рейок), столяр, не вимірюючи її ширини і не виконуючи жодних обчислень, виконує розмітки, показані на малюнку, після того проводить прямі ВВ1, СС1, ДД1, ЕЕ1. Чи правильно поступає столяр ? (Рисунок 4)
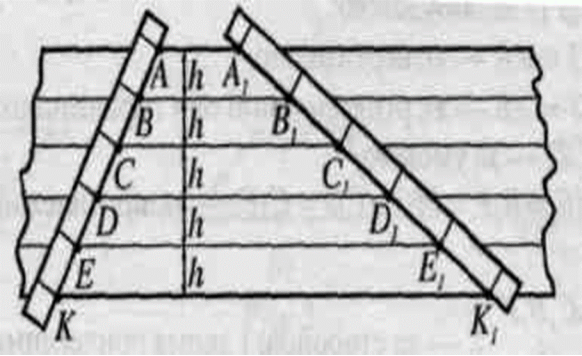
Відповіддю на поставлене питання у задачі послужить теорема Фалеса. Це теорема не звичайна, а авторська, названа в честь її творця і, до речі, людини, яка за переказами у свій час зуміла навіть зупинити війну.
Учитель. Отже, ми згадали основні геометричні істини, які допоможуть нам знайти відповідь на поставлене запитання.
Учитель. Формулювання теореми Фалеса подано в підручнику на сторінці 51 і звучить так:
паралельні прямі, які перетинають сторони кута і відтинають на одній із них рівні відрізки, відтинають рівні відрізки і на іншій стороні.
Які умови з прочитаного формулювання повинні виконуватися, щоб теорема була істинною?
(Доведення теореми вчителем).


Учитель. Ось такими міркуваннями ми підійшли з вами і до ще одного формулювання цієї теореми. Можливо ви й самі можете зробити невеличке узагальнення, виходячи з ваших попередніх відповідей?
- Первинна перевірка засвоєння знань
![]()
- Первинне закріплення знань
Вправа на побудову.
![]()
Алгоритм виконання (показано на екрані, виконують на дошці та в зошиті)
- Нехай АВ – даний відрізок (проведемо його довільно)
- Проведи довільний промінь АМ.
- Відклади на ньому за допомогою циркуля послідовно сім відрізків АС1, С1С2, С2С3, С3С4, С4С5, С5С6, С6С7.
- Проведи через точки С2 та С7 за допомогою косинця і лінійки дві паралельні прямі DС2 та ВС7.
- За теоремою Фалеса вони поділять відрізок АВ у заданому відношенні АD:DВ=2:5.
Висновок: таким способом можна ділити у заданому співвідношенні будь-які відстані.
Розв’язуємо задачу
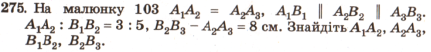
|
|
Розв’язання
Нехай А1А2=3х, В1В2=5х, тоді А1А2= А2А3=3х і 5х-3х=8, 2х=8, х=4. Отже, А1А2= А2А3=3∙2= 6 см, В1В2= В2В3=5∙2= 10 см. Відповідь: 6 см, 10 см. |
- Контроль і самоперевірка знань
Учитель перевіряє роботу в зошиті.
Учням пропонується оцінити свою роботу й записати оцінку в зошиті.
Форма для самооцінювання
|
Оцінка |
Правила, вивчені раніше |
Теорема Фалеса |
Усна задача |
Задача на побудову |
Задача на розв’язання |
|
Відмінно |
Знав всі |
Знаю і зрозумів теорему, можу довести самостійно |
Відповідь знайшов швидко |
Не виникало труднощів під час виконання |
Самостійно знайшов шлях для розв’язання |
|
Добре |
Лише деякі правила згадав згодом |
Зрозумів теорему, але ще складно її доводити |
Відповідь знайшов після обговорення з сусідом |
Під час виконання креслення допускав деякі помилки |
Задачу зрозумів після колективного обговорення |
|
Задовільно |
Складно було згадати правила |
Складно зрозуміти теорему |
Відповідь знайшов після допомоги учителя |
Складно було користуватися інструментами для креслення |
Задачу записав у зошит, але сам не зробив би. |
- Підбиття підсумків уроку. Рефлексія
Отже, сьогодні на уроці ми… (Вивчили теорему Фалеса, навчилися її застосовувати при розв’язанні задач, зрозуміли, як її можна використати для поділу відстані на задане співвідношення)
На уроці я... — дізнався... — зрозумів... — навчився... — найбільший мій успіх — це... — найбільші труднощі я відчув... — я не вмів, а тепер умію... — я змінив своє ставлення до... — на наступному уроці я хочу... (записують на заготовлених кольорових геометричних фігурках та зачитують)
- Інформація про домашнє завдання
Вивчити стор.55-56, виконати завдання:
середній рівень №270,
достатній рівень №276,
високий рівень №279.
Творче завдання: напиши п’ять причин, чим прославився Фалес.
Фалес Мілетський — багатий мудрець
Фале́с Міле́тський ( бл. 624 — 548 до Хрестової ери) — мислитель, математик, астроном, засновник іонійської школи філософії. На думку Валерія Бебика Фалес мав скіфо-дорійське походження, за іншими відомостями — фінікійське, тобто ханаанське.
Багато подорожував. Зокрема, навчався в Єгипті. Осівши в Мілеті, заснував там школу філософії. Був одним з учителів Піфагора.
Він передбачив сонячне затемнення (28 травня 585 до Хрестової ери). Йому належить заслуга у визначенні часу сонцестояння і рівнодення, у встановленні тривалості року в 365 днів, відкриття факту руху Сонця відносно зірок. Він вперше в історії науки використовує доведення теорем. Якщо землемірів задовольняла відповідь на питання «Як?», то Фалес, мабуть, першим поставив питання «Чому?» й успішно відповів на нього.
Фалес відкрив цікавий спосіб визначення відстані від берега до видимого корабля. Йому приписують також спосіб визначення висоти різних предметів, зокрема пірамід, за довжиною тіні, коли сонце піднімається над горизонтом на 45 градусів.
У «Політиці» Аристотеля є уривок про те, як Фалес за допомогою спостережень за зірками передбачив врожай олив та використав цей факт для власного збагачення. Таким чином він показав, що філософи здатні стати багатими, якщо захочуть.













про публікацію авторської розробки
Додати розробку