Урок геометрії у 8 класі на тему "Теорема Піфагора"

Урок геометрії у 8 класі

для дистанційного компоненту освітнього процесу в закладах загальної середньої освіти

 

Вчитель  Леонова Л.М.

Тема: Теорема Піфагора

 

Мета:

Навчальна:

• систематизувати відомості про прямокутний трикутник;
• розглянути теорему Піфагора як джерело надзвичайних математичних відкриттів;
• формувати значущість, практичний аспект теореми Піфагора як для геометрії, так і для математики вцілому;
• підвищувати рівень мотивації навчання.

Розвивальна:

• розвивати уяву, логіку, пам'ять учнів;
• розвивати пізнавальний інтерес учнів;
• розвивати уміння та навички самостійного здобуття знань, уміння застосовувати їх для розв’язання нових пізнавальних та практичних завдань;
• розвивати здатність працювати у різноманітних групах, виконуючи різні соціальні ролі, навички самооцінки та самоконтролю;
• розвивати уміння здійснювати дослідницьку діяльність;
• розвивати уміння працювати з інформаційними джерелами.

Виховна:

• виховувати спостережливість;
• лідерські якості;
• науковий підхід;
• інтерес до математики, практичну спрямованість предмету;
• толерантність, вихованість.

 

Тип уроку: засвоєння нових знань.

 

 

Хід уроку

1.Організаційний момент.

 

2. Мотивація навчальної діяльності учнів.

В сучасному світі без реклами неможливо жити.

Тому вашій увазі «Математична реклама» (на слайді зображені геометричні фігури, в яких можна побачити трикутники). Повяжіть ці зображення і скажіть, яку геометричну фігуру рекламовано.

Отже, трикутники можна побачити в планіметричних і просторових фігурах, в практичній діяльності: будівництво, архітектура тощо.

Чому саме трикутники? Бо кожний многокутник можна розрізати на кілька трикутників. Тому трикутники в геометрії відіграють таку важливу роль, як атоми у фізиці, як цеглини в будинкувони. А ще мають дуже важливу властивість – жорсткість.

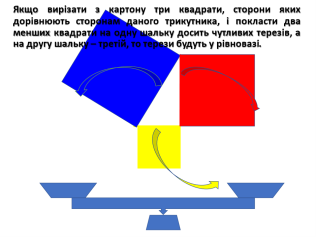
Якщо зібрати з окремих планок трикутник і чотирикутник, то виявиться, що

чотирикутник неважко деформувати: змінити кути, не змінюючи довжин сторін, а трикутник деформувати не вдається. Тобто три сторони трикутника однозначно визначають його кути!

Знаючи, що з усіх многокутників тільки трикутник фігура жорстка, ажурні конструкції виготовляють так, щоб вони мали якомога більше трикутників.

 

 

 

3. Актуалізація опорних знань учнів. 

Метод «Мікрофон»

А які види трикутників ми знаємо?

 

Серед них найпочесніше місце займає прямокутний трикутник.

 

(повторення відомостей про прямокутний трикутник)

• Прямокутним трикутником називається трикутник, який …..
• Сторона прямокутного трикутника, яка лежить проти прямого кута ….
• Сторони прямокутного трикутника, які утворюють прямий кут  …
• Сума всіх кутів трикутника дорівнює…..
• Сума гострих кутів прямокутного трикутника дорівнює …
• У прямокутному трикутнику не може бути …. кута.
• Катет, що лежить проти кута 30°, дорівнює ….
• Прямокутний трикутник з рівними катетами …
• Гострі кути прямокутного, рівнобедреного трикутника …
• Висота прямокутного трикутника, проведена до гіпотенузи є середнім пропорційним між проекціями …. (катетів на гіпотенузу)
• Катет  прямокутного трикутника є середнім пропорційним між гіпотенузою і .. (його проекцією на гіпотенузу)

 

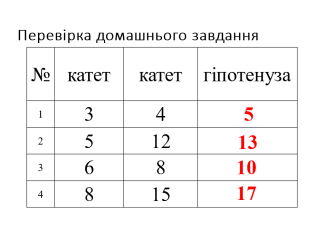
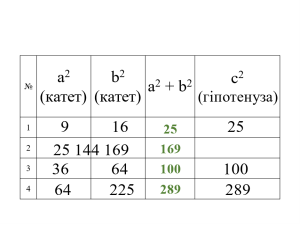
4. Перевірка домашнього завдання.

Обговорення домашньої практичної задачі, при виконанні якої учні креслили два довільні прямокутні трикутники та вимірювали за допомогою лінійки довжини сторін, порівнювали квадрат гіпотенузи із сумою квадратів катетів. Що ви помітили? Як ви вважаєте: це випадковість чи закономірність?

 

5. Повідомлення теми, мети та завдань уроку.

 

Епіграф: «Вчись усьому, що потрібно знати, і тоді будеш вести спокійне життя. Початок є половина всього».(Піфагор)

 

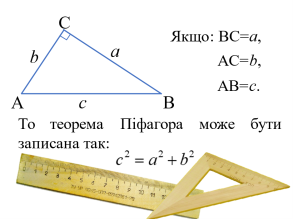
6. Вивчення нової теми.

 

(Перегляд відео-файлу   https://www.youtube.com/watch?v=YRBaVlC4_x0   )

 

 

Хвилинка відпочинку

 

Біографія вченого, оповита легендами і гіпотезами. Нажаль, всі відомості про «найбільшого еллінського мудреця», зі слів Геродота, ґрунтуються на працях його послідовників. Хто ж такий Піфагор?

 

(Перегляд відео-файлу   https://www.youtube.com/watch?v=4KMuqRpibbw)

 

Народився Піфагор Самоський на о. Самосі, біля узбережжя Малої Азії приблизно 580 років до нашої ери. Він із знатного роду. Його батьки за пророчеством Бога Аполлона надають сину гарну освіту та виховання. Він отримує знання основ музики та живопису, вивчає природу, таємниці чисел, навчається астрології, медицині.

Піфагор перший назве Всесвіт «Космосом», відкриє гармонійні співвідношення в музиці, розів’є вчення про число, введе термін «Філософ». Він навчався у Фалеса, засновника першої в історії філософської школи. Отримував знання в Єгипті, Вавилоні, Індії.

Повернувшись у Грецію, Піфагор оселився в місті Кротоні, у якому створює школу, яка діє майже тридцять років і здобуває велику популярність досягненнями в галузі математики. Статут школи був дуже суворим. Потрапити до школи Піфагора могли тільки розумні, кмітливі та старанні учні. Греки вважали за честь навчатися в Піфагорійській школі. Емблемою союзу і розпізнавальним знаком піфагорійців була пентаграма – правильний п’ятикутник. Діагоналі п’ятикутника утворюють зірку, яку піфагорійці вважали символом здоров’я.

Доля Піфагора, як і його школи трагічна. Існує три версії загибелі вченого: від голодування,

 при пожежі в Школі,

та під час вуличних суточок.

 

 

Різні способи доведення теореми Піфагора та цікаві історичні факти пов’язані з теоремою

.

 

(Перегляд  відео- файлу  https://www.youtube.com/watch?v=YyFFE-tbfkk)

 

Теорема Піфагора має народну назву «Піфагорові штани на всі сторони рівні» завдяки математику – філософу Евкліду. Креслення, яке застосовується при доведенні цієї теореми жартівливо назвали «Піфагорові штани».

 

Єгипетський трикутник

Про те, що трикутник зі сторонами 3, 4, 5 - прямокутний, знали єгиптяни ще за 2000 років до нашої ери і користувалися цією властивістю для побудови прямих кутів.

 

Теорема Піфагора має і інші народні назви:

• У Франції і деяких областях Німеччини в середні віки її називали „віслюків міст” (вважали, що коли учень не розуміє теорему, символічно не пройде через неї, то він "справжній віслюк")
• "гетакомба" - сто биків.
• У математиків арабського Сходу ця теорема одержала назву „теореми нареченої».

 

 

«Застосування теореми Піфагора»

 

 

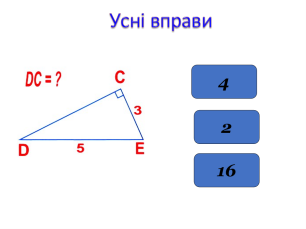
Особливе значення посідають в історії математиці Піфагорові трійки. Це такі три числа у яких квадрат одного дорівнює сумі квадратів двох інших (наводяться приклади чисел)

Єгипетські трикутники — це такі прямокутні трикутники сторони яких пропорційні числам 3, 4 і 5

 

 

7.  Відповідь на проблемне питання.

У чому полягає причина популярності теореми Піфагора?

Популярність теореми триєдина – це краса, простота, значущість.

 

8. Оцінювання учнів.

 

9. Підсумок уроку. Рефлексія.

Сьогодні ви зробили ще один крок, щоб вважати себе людиною розумною... Навіть єгипетські жерці, віддаючи своїх дітей для навчання мистецтву, хотіли передусім, щоб вони вивчали геометрію. А Гіппократ вважав, що для того, щоб стати добрим лікарем і знати як розміщені органи, слід вивчати геометрію. Один із послідовників Сократа, опинившись на безлюдному острові та побачивши на піску накреслені геометричні фігури, радісно вигукнув: "Я бачу геометричні малюнки, отже, я бачу сліди людей розумних.

Вам іти у світ, вам доводити ще не одну математичну і не одну життєву теорему. Можливо, з часом теорема Піфагора буде здаватися вам до сміху простою. Але сьогодні ви подолали певний рубіж, ви стали розумнішими на цілу теорему - на теорему Піфагора, цікаву, могутню і Вічну. Дякую вам за співпрацю. Ви всі були молодці.

 

А зараз я пропоную скласти СЕНКАН до слова ПІФАГОР

А ще цікаво, які із висловлювань Піфагора вам сподобалися найбільше?

 

Домашнє завдання.

 

1. Вивчити теорему Піфагора.

 

2. Виконати тести за посиланням  https://naurok.com.ua/test/teorema-pifagora-1044769.html
3. Розв’язати 1 із запропонованих задач:

 

Задача 1

У народі кажуть «Без верби і калини нема України». Здавна в нашій місцевості на обійстях садили ці рослинисимволи. Знайдіть висоту верби, якщо довжина тіні, яку відкидає це дерево, дорівнює 4 м, а відстань від вершини стовбура до кінця тіні – 5 м. Відповідь: 3 м.

Задача 2

За 40м одна від однієї ростуть дві ялинки. Ви заміряли їх висоти: виявилося, що одна із них має висоту 31м, а інша, молода – 6м. Чи можете ви обчислити, якою є відстань між їхніми верхівками?

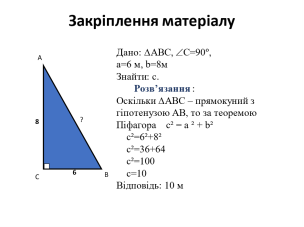
Задача 3

Знайти довжину драбини, прикладеної до будинку, якщо один її кінець находиться на відстані 4м від будинку, а другий на  зіткненні стіни і даху. Висота будинку дорівнює 8м.

Задача 4

На березі річки тополя росла та вітру порив її стовбур зламав.

Тополя упала і стовбур її кут прямий з течією річки утворив.

Памятайте у тому місці ріка 4 фути була шириною.

Верхійвка схилилась до краю, залишивши 3 фути всього під водою.

Прошу тепер швидше скажіть мені ви, тополя якої була висоти ?

Задача 5

Над озером тихим

Висотою із пів фута підіймалася лотоса квітка, яка росла одинокою.

Та вітер скаженим поривом

Відніс її в бік.

І не стало видно квітки над водою.

Знайшов її рибалка ранньою весною

В двох футах від місця її росту.

І так, пропоную я вам запитання:

Яка в цьому місці глибина озера?

Задача 6

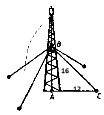Вертикальна вежа підтримується чотирма канатами, які прикріплені до неї на відстані 16м від землі і на відстані 12м від основи вежі. Скільки метрів канату потрібно для укріплення вежі, якщо на вузли пішло 10м?