План-конспект уроку

Предмет: Геометрія

Тема програми: Аксіоми стереометрії.

Взаємне розміщення прямих у просторі.

             Тема       уроку:       Основні       поняття

стереометрії. Аксіоми стереометрії.

Мета уроку.  

навчальна: дати уявлення

про стереометрію як частину геометрії, домогтися засвоєння аксіом стереометрії, узагальнити відомості про просторові фігури;

виховна: виховувати культуру праці, працелюбність, бережне

відношення до майна; 

розвиваюча: розвивати технічне мислення, просторову уяву,

пам`ять, сприяти розвитку координації рухів; здібностей учнів та їхнього інтересу до геометрії.

Обладнання: Персональний комп’ютер, проектор, програма Power Point, роздатковий матеріал (зображення картин, робочі листи), презентація, моделі многогранників.

Тип уроку: засвоєння нових знань.

Вид уроку: бесіда

План уроку

I.                  Організаційний момент.

II.               Перевірка домашнього завдання.

III.            Оголошення теми, мети, завдань уроку.

IV.            Вивчення нового навчального матеріалу. V. Засвоєння знань і вмінь.

VI.                Підбиття підсумків уроку.

VII.            Домашнє завдання.

          

Хід уроку

І. Організаційний момент.

Привітання, перевірка відсутніх на уроці.

ІІ.        Перевірка домашнього завдання.

(домашнім    завданням було повторити    основні       поняття

планіметрії)

Викладач роздає робочі листи з тестовими завданнями.

Виконання тестових завдань.

1)    Які з наведених фігур не є основними фігурами планіметрії?

1)    Пряма;

2)    Куля;

3)    Точка;

4)    Площина;

2)    Яке з наведених тверджень є аксіомою шкільного курсу геометрії?

1)    Сума суміжних кутів дорівнює 180°.

2)    Яка б не була пряма, існують точки, що належать цій прямій і точки що не належать їй.

3)    Дві прямі на площині називаються паралельними, якщо вони не перетинаються.

4)    Через кожну точку прямої можна провести на площині перпендикулярну до неї пряму і до того ж тільки одну.

3)    Яке з наведених тверджень є теоремою з шкільного курсу геометрії?

1)    Вертикальні кути рівні

2)    Через будь які дві точки можна провести пряму і тільки одну.

3)    Кожний відрізок має певну довжину, більшу від нуля.

4)    Трикутник називається рівнобедреним, якщо дві його сторони рівні.

4)    Яке з наведених тверджень правильне?

1)    Через три точки можна завжди провести пряму і тільки одну.

2)    Через три точки в жодному разі не можна провести прямої.

3)    Через одну точку можна провести 1 000 000 прямих.

4)    На площині не існує інших точок, крім тих що належать певній прямій.

ІІІ. Оголошення теми, мети, завдань уроку

Вступне слово викладача

Викладач говорить про місце геометрії у математиці та її особливості які пов’язують геометрію з мистецтвом.  

Серед інших розділів математики геометрія відрізняється однією особливістю – це нерозривне з’єднання живого уявлення і логіки. Уява більше належать мистецтву, а 

логіка - науці. Як дві сторони однієї медалі, але якщо немає однієї із сторін

–        немає          і         справжньої          геометрії. Німецький педагог Адольф Дістервех, сказав у свій час:

«Більше приносить користі розгляд одного і того ж предмету з 10 різних сторін, ніж          розгляд       10      різних предметів з однієї сторони».  

Тому ми сьогодні з вами повинні подивитися на геометрію з різних сторін. Спочатку як на науку, потім як на мистецтво.

Отже, сторона перша – наука. Викладач задає питання учням. 

1.     Геометрія – це наука, яка …

Очікувана     відповідь:   отже,         це наука,     яка    складається         з           вивчення геометричних фігур та їх властивостей.

2.     З яких двох розділів складається шкільний курс геометрії?

Очікувана відповідь: планіметрія і стереометрія

3.     Чим вони відрізняються один від одного?

Очікувана відповідь:

Планіметрія (від латин. Planum – площина і грец. Metreo – вимірюю, у буквальному перекладі «вимірювання плоского») – це розділ геометрії в якому вивчають фігури на площині.

(викладач доповнює)

Стереометрія (від грец. Stereos – просторовий і metreo – вимірюю, тобто буквально «вимірювання просторового») – це розділ геометрії, у якому вивчають фігури в просторі.

Отже, ми можемо записати тему нашого уроку: «Основні поняття стереометрії.           Аксіоми стереометрії». 

                                                                                                                                                                                                                                                                                                  ІV.           Вивчення          нового

навчального матеріалу

Викладач задає питання учням:

1.     Які саме фігури вивчає геометрія?

Очікувана відповідь: трикутник, квадрат, ромб, пряма, точка…

2.     Поясніть мені, будь ласка, навіщо нам вивчати ці фігури, чи можемо ми в природі зустріти куби і кулі, прямі і точки?  

Очікувана відповідь: яблуко і т. д.

Але ж, в природі не існує ідеальних фігур, вони є грубою подобою до ідеальних геометричних фігур. 

3.     Що простіше вивчати, ідеальні об’єкти чи недосконалі?

Очікувана відповідь: ідеальні

Таким чином,         геометрія   –        це математична ідеальна      модель навколишнього світу. І пізнаючи та

вивчаючи ці моделі людина тим самим пізнає навколишній світ. Але, всьому в природі є свій початок, так давайте розберемось який початок у геометрії?

Очікувана    відповідь:   перші геометричні відомості знали ще з давніх давен, Єгиптяни, волиняни, греки, але ці відомості були різного характеру, і були отримані в результаті спостережень і практичного досвіду.

                                                                                                                            Вище     призначення     математики     -

знаходити порядок в хаосі, який нас оточує.

сказав американський математик Ноберт Вінер

І саме з цією метою вчені працювали над систематизацією всіх геометричних знань.

(викладач викликає учня до дошки з повідомленням про працю грецького вченого Евкліда).

             Доповідь        учня:        З        метою

систематизації геометричних знань в ІІІ ст. до н.е. грецький вчений Евклід зібрав наявний на той час матеріал із стереометрії і виклав його в своїй відомій праці

«Основи» (на рос. Мові – «Начало»), першу і найкращу енциклопедію елементарної математики. Перед Евклідом стояла проблема – як зібрати в одне ціле ті знання, які на той час були відомі. І він вирішив цю проблему       за допомогою аксіом, понять із яких і будується весь курс геометрії. 

Згадайте 7 клас, ви з яких понять почали вивчати геометрію?

Очікувана відповідь: точка, пряма…

А зараз в стереометрії познайомимось з поняттям – площина.

Отже, на основі спостережень за цими поняттями Евклід сформував істину, яка не потребує доведення. І як вона називається? 

Очікувана відповідь: аксіома або постулат.

Евклід розділяв ці поняття, а в даний час вони значать практично одне і теж.

А ще які твердження ви вивчали в геометрії?

Очікувана відповідь: теореми, леми, властивості і тд…

Тобто всі інші твердження вже безпосередньо виводяться або доводяться із основних понять.

Отже, найцінніше, що дав світу Евклід - це аксіоматичний підхід до вивчення не тільки геометрії, але і інших наук.

І сьогодні на уроці ми подивимось як геометрія і аксіоматичний підхід допомагають вивчати навколишній світ.

(викладач пропонує вирішити практичну задачу)

Задача:

Уявіть що ви як Робінзон Крузо 

раптом опинилися   на      безлюдному острові.

Змайструйте для себе стілець  з тих матеріалів, які є під рукою

(викладач роздає набори конструктори,

коли діти почали майструвати, проходить по класу, перевіряє та коментує роботи учнів).

На якому стільці буде зручніше сидіти: на тому, що на трьох рівних ніжках, чи тому, що на чотирьох різних? Очікувана відповідь: на тому, що на рівних ніжках.

Формулювання першої аксіоми стереометрії та ілюстрація малюнка до неї в робочих листах:

С1:

Через будь–які три точки, що не лежать на одній прямій, можна провести площину, і до того ж тільки одну.

 

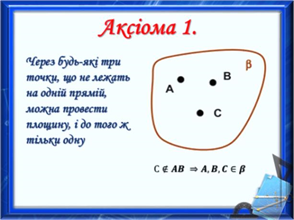
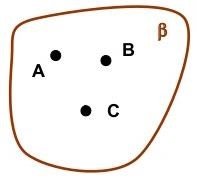
С ∉ АВ ⟹ А, В, С ∈ 𝛽

Задача.

Аліса прийшла в гості до Болванчика не сповна розуму.

Дивлячись на крючки, прибиті до стіни і на      вішалки       –        плечики,      Аліса замислилась…

Як повісити їй пальто так, щоб воно не пом’ялось?  

Як би ви зробили і чому саме так?

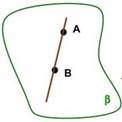
Викладач формулює аксіому:

С2:

Якщо дві точки прямої лежать у площині, то і вся пряма лежить у цій площині.

 

Задача.

З третьою аксіомою ми зустрічаємось коли складаємо фігури з аркушів паперу.

Скажіть, будь ласка, що являє собою утворена лінія вигину?

(викладач формулює аксіому, дає завдання замалювати до неї малюнок в робочих листах).

С3:

Якщо дві площини мають спільну точку, то вони перетинаються по прямій, яка проходить через цю точку.

Запитання до учнів:

1.  Де в житті доводиться зустрічатися з цією аксіомою, наведіть приклад, подивіться навколо себе?

                                                     

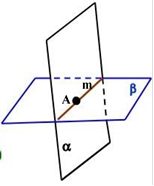
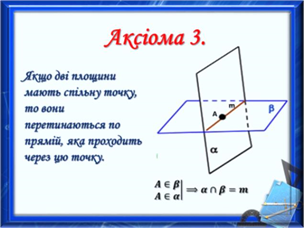
𝐴 ∈ 𝛽| ⟹ 𝛼 ∩ 𝛽 = 𝑚   

𝐴 ∈ 𝛼

Отже, ми вже уявляємо, як можна вивчати навколишній світ за допомогою геометрії і тепер для вас не складно буде відповісти ще на одне питання.

Коли три горобці, які сиділи на одному столі, після зльоту знову опиняться в одній площині?

Очікувана відповідь: три горобці завжди знаходяться в одні площині.

Викладач    дає     завдання переконати її.

Очікувана відповідь: аксіома 1.

                                                                                                                                              Отже,      провівши     ланцюжок

певних висновків довели, спираючись на якісь правила і аксіоми, своє твердження. Такі міркування в математиці називаються доведеннями.

В чому ж полягає перша користь від занять геометрією?

Очікувана відповідь: ці заняття вчать нас буди переконливими в суперечці, доводити правоту.

Як ви думаєте, навіщо ми малювали ілюстрації до аксіом?

Уявіть,         якщо вам    потрібно замовити незвичайний стіл майстру, який опис дасть більш точно уявити ваше замовлення? Словесний чи малюнок?

А який саме малюнок несе більше інформації для майстра, схематичний чи від руки аби як?

Очікувана відповідь: схематичний

Тому, дуже важливо вміти схематично зображувати просторові фігури, на аркуші паперу.

Але ще важливо бачити об’єм на площині. Для цього потрібно мати гарну уяву.

Отже, друга сторона геометрії  - мистецтво.

Одного разу німецький математик Давид Гільберт сказав про одного із учнів своїх:

«Він став поетом  - для математики у нього занадто мала уява».

(викладач пропонує провести тест, який визначить     на      скільки       добре          розвинута просторова уява в учнів).

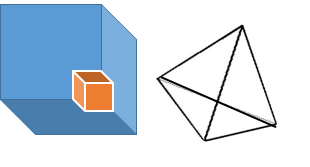
Тест на уяву.

На екрані представлені два малюнки. Необхідно записати в робочі листи, якомога більше версій, що на них зображено.

Запишіть декілька варіантів, що саме ви бачите.

Очікувана   відповідь:   піраміда чотирикутна, прямокутний        паралелепіпед якому приклеїли куб на кут., і т. д.

Результати тесту.

5-6 – уява розвинуто на відмінно

3-4 - добре

0-2 – потрібно розвивати просторову уяву

Сьогодні ми будемо вчитися розвивати уяву.

Одним із способів зображення об’ємних     фігур           є        паралельна проекція, яка нагадує створення тіні від предметів в сонячний день. І якщо ми будемо брати різні напрямки проектування або різні площини, то будемо отримувати різні зображення однієї і тієї ж фігури.

Завдання.

Уявіть, що у вас в руках знаходиться квадрат, зверху на нього падає проміння сонця, покрутіть його, уявіть яка буде тінь і замалюйте в зошитах.

1.     Яку тінь ви отримали? (викликати до дошки учня, щоб той намалював.)

2.     Яка тінь дає об’єм? 

Люди з давніх давен намагаються втиснути об’єм в площину і зобразити навколишній світ на скалі чи полотні. Художники удосконалюють свою майстерність, щоб створити ілюзію об’єму в своїх картинах.

(викладач демонструє картину венгерського художника Іштван Ороса «Колодязь», учень розповідає коротку історію картини).

Картина була написана на честь сторіччя з дня народження іншого голландського художника, засновником математичного мистецтва, який писав про вивчення

математики, як про прогулянки по прекрасному      садку,          де      ні       що     не повторюється. Ворота в лівій частині картини відділяють математичний сад, який знаходиться в нашому мозку, від навколишнього      світу.          Звати         цього художника – Моріс Корнеліус Ешер.  

Лице    цього          художника зображено на даній картині. Щоб його побачити, нам потрібно вийти із площини в простір. Для цього скористайтеся циліндрами.

(викладач пропонує поставити циліндри     в        середину     колодязя, зображеного на картині і побачити у відображенні, портрет). 

Наступною картиною буде М.К. Ешер «Бельведер», далі картина «Водопад».

Ця картина написана на основі неможливого трикутника, вигаданого англійським

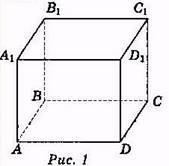математиком Роджером Пенроуза.  (викладач обговорює з учнями неможливий трикутник).

V. Засвоєння знань і вмінь

(викладача викликає учнів до дошки та дає їм завдання)

Завдання 1.

Користуючись рис.1, вкажіть:

а) спільні точки верхньої і передньої граней;

б) пряму перетину площин задньої і нижньої граней; 

в) спільні точки площин граней АВВ₁А₁, і Α₁Β₁С₁D₁;

г) пряму перетину площин граней Α₁Β₁С₁D₁ і ВВ₁С₁С.

Завдання 2.

Користуючись зображенням куба на рис.2, вкажіть точки, які:

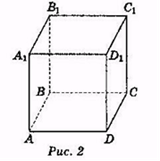а) не належать передній грані; 

б) належать верхній грані;

б) належать грані ABCD;

г) не належать грані А₁В₁ВА.

Завдання 3

1.             Користуючись рис.1, вкажіть, яку площину визначають прямі:

а) АВ і АD;     б) BС і СС₁;     в) DC і СС₁; г) А₁В₁ і В₁А.

2.             Користуючись зображенням куба на рис.2, доведіть, що можна провести площину через прямі:

а) АС і СС₁;    б) AD і DC₁.

VІ. Підбиття підсумків уроку  (проводиться у вигляді рефлексії) Рефлексія:

1.                  Я дізнався…

2.                  Я навчився…

3.                  Мені сподобалось… VIІ. Домашнє завдання 

1.       Завдання за підручником:  §20, № 740, 744;

2.       Додаткове завдання: скласти неправильний трикутник. 

Кожному учневі дісталась розгортка неможливого трикутника. Ваше завдання

виготовити модель і проаналізувати її, знайти той кут, під яким потрібно буде подивитися на трикутник одним оком, щоб його побачити. Пам’ятайте, що все у ваших руках і якщо ви будете мати гарну уяву, володіти достатнім багажем знань та великим бажанням вирішити будь яку проблему, то все неможливе стане –

можливим.