Конспект уроку з математики для 6 класу на тему: "Множення раціональних чисел "
Тема уроку: Множення раціональних чисел
Мета уроку: навчити учнів множити раціональні числа, знаходити значення
виразів, розвивати навички усної лічби, математичну мову,
виховувати інтерес до нових знань і прагнення їх здобувати.
Тип уроку: урок засвоєння нових знань.
Хід уроку:
- Організація початку уроку.
- Вивчення нового матеріалу.
1.Згадати означення раціональних чисел. Навести приклади.
2.Які дії ми вже вміємо робити над раціональними числами?
3.А скажіть, будь ласка, якою дією можна замінити суму кількох однакових
доданків?
Наприклад, 5+5+5=53; 7+7+7+7=74
4.Як називаються числа при множенні? З'являється питання: а чи можна
множити додатнє число на від'ємне? від'ємне число на від'ємне?
Виявляється, що суму кількох однакових від'ємних чисел також можна
замінити добутком.
Що означає помножити, наприклад, число -6 на 4? Це означає знайти
суму 4-ох доданків, кожен з яких дорівнює -6:
(-6)4=(-6)+(-6)+(-6)+(-6)=-24; отже, (-6)4=-24.
Щоб виконувався переставний закон множення, вважають, що 4(-6)=-24
Міркуючи так само щодо чисел -15 і 10, маємо:
(-15)10=-150 і 10(-15)=-150.
5.Сформулювати правило множення від'ємного і додатнього чисел.
Приклади:
(-4)34=-136; (-2)/39/22=(-3)/11;
6(-1)/36=(-1)/6; ½ (-4)/3=-(2)/3;
6. №1244( стор.217)- усно 1 стовпчик;
№1245(непарні)
-
10(-4)=-40; 5) -
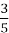5=-3;
3) -70,3=-2,1; 7) 2,3(-
)=-0,575.
7. Сформулюємо правило множення двох від'ємних чисел.
Приклади:
(-3)(-4)=12; (-3)/7(-14)/5=6/5;
(-1,5)(-6)=9; (-2,4)(-1,2)=2,88.
Чому саме за такими правилами множать від'ємні числа, стане зрозуміло
пізніше. У загальному вигляді ці правила записують так:
(-а)(-b)=ab;
(-а) b=-ab.
Знак добутку визначається знаками множників, як показано в таблиці 3:
|
Знак числа A |
Знак числа B |
Знак A*B |
|
+ - - + |
+ - + _ |
+ + - -
|
№1248
- -4(-25)=100; 3) -0,04(-2,5)=0,1; 5) -0,6(-5)=3;
- -12(-100)=1200; 4)-1,3(-0,01)=0,013; 6) -0,01(-130)=1,3.
Звернемо увагу на окремі випадки множення. Ɐ є Q завжди:
а0=0а=0;
а1=1а=а;
а(-1)=(-1)а=-а;
№1257 (усно)
8. Раніше вчені намагалися обґрунтувати правило множення від'ємних
чисел, хотіли зрозуміти, чому (-а)(-b)=ab. Наводили різні обґрунтування
цього правила, але вони згодом виявлялися непереконливими. Тому
протягом кількох століть правила множення і ділення від'ємних чисел
вважали незаконними, а самі від'ємні числа називали хибним
абсурдними, несправжніми. Тільки згодом учені зрозуміли, що такі
правила слід не виводити з інших, уже відомих правил, а визнати їх
правильними за домовленістю. У сучасній математиці рівність
(-а)(-b)=ab приймається без обґрунтувань. Тільки за такої домовленості
раціональні числа стають корисними і зручними у застосуванні.
Гра на відпочинок ( 5 хв.)
- 1) Хто з птахів може розвивати швидкість до
360 км/год?
А. Сокіл; В. Орел; С. Страус; D. Горобець
- 2) Чиє серце може важити 600-800 кг?
А. Зубр; В. Слон; С. Бегемот; D. Кит
- 3) Скільки видів риб у Мертвому морі?
А. 10 000; В. Жодного; С. 1000; D.1 000 000
- 4) У якого птаха довжина кроку може досягати 8,5 м?
А. Сорока; В. Кенгуру; С. Страус; D. Горобець
- 5) Найбільша одиниця вимірювання площі.
А. 1 а; В. 1 га ; С. 1 
; D. 1 д
- 6) Скільки кілограмів має один центнер?
А. 10 000; В. 10; С. 1000; D.100
-
7) Як називається
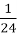частина доби?
А. Година; В. Хвилина; С. День; D. Секунда.
- 8)Яким інструментом вимірюють величину кута?
А. Лінійка; В. Лекало; С. Транспортир; D. Циркуль
- 9) Чому дорівнює одинадцять у квадраті?
А. 22; В. 101; С. 121; D.111
- Закріплення матеріалу.
№1261, №1269, №1272(1,2), №1282*(1)
- Домашнє завдання: §28 перемалювати таблицю 14 в зошит( за підручником Н. А. Тарасенкова)
ЗНОБ-НОВГОРОДСЬКИЙ ОПОРНИЙ ЗАКЛАД ЗАГАЛЬНОЇ
СЕРЕДНЬОЇ ОСВІТИ І-ІІІ СТУПЕНІВ
ЗНОБ-НОВГОРОДСЬКОЇ СЕЛИЩНОЇ РАДИ
СЕРЕДИНО-БУДСЬКОГО РАЙОНУ СУМСЬКОЇ ОБЛАСТІ
про публікацію авторської розробки
Додати розробку