Конспект уроку з математики для 6 класу з теми «Властивості множення раціональних чисел»

Конспект уроку з математики

 для 6 класу з теми «Властивості множення раціональних чисел»

Вчитель: Старостенко С.Б.

 

Тема: Властивості множення раціональних чисел

Мета: повторити відомі учням властивості множення натуральних та дробових чисел, поширити їх на множину раціональних чисел; вдосконалювати вміння виконувати дію множення раціональних чисел; розвивати навички усного рахунку, вміння узагальнювати та систематизувати матеріал; виховувати інтерес до нових знань і прагнення їх здобувати.

Обладнання: дошка, роздавальний матеріал, таблиці

Тип уроку: систематизація та узагальнення знань, умінь та навичок

 

ХІД УРОКУ

 

І. Перевірка домашнього завдання

Зошити перевірити перед уроком. На дошці з коментуванням розібрати виконання №1092, пояснити №1098.

ІІ. Актуалізація опорних знань

• На дошці записаний великий ланцюжок математичних термінів. Прочитайте їх та поясніть.

Цілінатуральнівід’ємніраціональніпротилежні

• Отже, всі числа, які нам відомі на сьогоднішній день, називаються…?
• Що вам відомо про нові числа, про від’ємні?

Історична довідка

Від’ємні числа виникли в Китаї в І ст до нашої ери у зв’язку з розв’язуванням рівнянь. Оскільки в ті часи знаків плюс та мінус не було, то від’ємні числа позначали іншим кольором на відміну від додатних. Додатними числами позначали майно, прибуток, наявні гроші. Їм раділи та зображали червоним кольором (китайці їх називали «чен»), від’ємними числами позначали борг, збиток, тому зображали їх чорним кольором (називали їх «фу»).

В ХІІІ столітті від’ємні числа в Китаї стали зображувати цифрами, перекресленими похилою рискою справа наліво.

В V – VІ ст. індійці-математики використовували від’ємні числа в задачах на рух, виграші, програші, а в деяких задачах мова йшла про момент зустрічі в минулому та майбутньому.

 В Європі вперше про від’ємні числа згадав італійський математик Леонардо Пізанський (Фібоначчі, ХІІ-ХІІІ ст.). Німецький математик Михайло Штіфтель (ХVІ ст.) називав від’ємні числа «числами, меншими за ніщо, тобто меншими від нуля. Він писав: «Нуль міститься між істиними та абсурдними числами». Довгий час від’ємні числа не визнавали, їх вважали несправжніми, фіктивними.

 Знаки «+» та «-» для позначення додатних і від’ємних чисел ввів в кінці ХV ст. німецький математик Відман.

 Наукове обґрунтування від’ємних чисел було дано в ХІХ ст.

 

• Які дії ви вмієте виконувати з раціональними числами?
• Як додати два числа з різними знаками?
• Як додати два від’ємних числа?
• Як знайти добуток двох від’ємних чисел?
• Як помножити два числа з різними знаками?

 

Усні вправи

Обчислити:

-7∙8;   -6∙(-5);  -2-3;   -3+5;   68∙0,5;

-6∙10;   -0,01∙(-34);  -2∙(-3);  -3∙5;   0,5∙68;

3∙(-0,7);  -5,8∙100;  4-8;   -6-7;   4∙25∙0,4;

4∙(-0,02);  0∙(-35,7),  4∙(-8;)   -6∙(-7)  0,5∙28∙2.

 

ІІІ. Узагальнення знань

 

Вивчивши алгоритм виконання будь-якої математичної дії, ми неодмінно повинні знайти відповідь на запитання: «А чи не можна цю дію за даним алгоритмом виконати більш зручним способом?»

Виконанню обчислень нам завжди допомагали основні властивості. Які? (Переставна, сполучна, розподільна.) Але їх ми застосовували для натуральних та дробових чисел, чи будуть вони справедливі для раціональних чисел? Давайте перевіримо це.

 

1. Виконати дії: (Біля дошки працює 2 учнів.)

-2,9∙(-1,3);    (-1,3)∙(-2,9);

5,1∙(-0,12);    (-0,12)∙5,1;

(-2∙(-10))∙5.    -2∙((-10)∙5).

Висновок: Для раціональних чисел справедливі переставна та сполучна властивості.

 

a∙b=b∙a;

(a∙b)∙c=a∙(b∙c).

 

 2. Продовжіть запис, використовуючи переставну властивість множення:

  a∙0=…;  1∙a=…;  -1∙a=…

 

 3. Проблемні питання:

1. Чи можна записати підряд 17 цілих чисел так, щоб добуток будь-яких чотирьох сусідніх чисел був від’ємним, а добуток всіх чисел додатним?

2. Визначте знак добутку (-1)∙(-2)∙(-3)∙(+5)∙(-7,5).

 

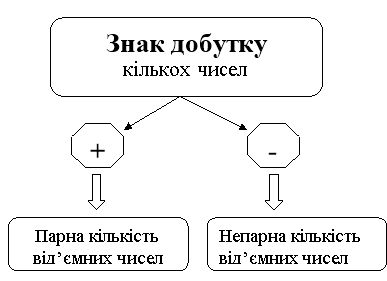
Знак добутку кількох раціональних чисел, відмінних від нуля, залежить тільки від кількості від’ємних множників:

а) якщо їх парне число, то знак добутку «+»;

б) якщо їх непарне число, то знак добутку «-».

_

 

IV. Удосконалення вмінь

Усні вправи

1. Додатним чи від’ємним буде добуток:

 а) трьох від’ємних чисел;

б) двох від’ємних і трьох додатних чисел;

в) одного додатного і трьох від’ємних чисел;

г) чотирьох від’ємних чисел?

2. Знайти знак добутку:

 №1156, №1157

3. Виконати множення:

 -3∙0;   -19∙1;   0,25∙(-3)∙(-4);

0∙13;   1∙(-27);  -1,25∙(-3)∙(-8);

-5∙(-17)∙0;  15∙(-4)∙(-25);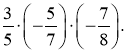 

Письмові вправи

№1166 а) (-7)∙(-8)∙0,5=28;  №1168 а) (-3)∙20∙(-8)∙0,5=240;

  б) 2,5∙(-6)∙40=-600.    б) 12∙(-5)∙(-2)∙(-0,5)=-60.

 

№1169 а)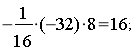

  б)

Відповіді в хаотичному порядку подано на дошці.

4. Розв’яжіть рівняння:

а) -3,2∙х=0;  б) -3,2∙(х-2)=0;   в) (х-3)∙(х+0,5)=0.

5. Визначте знак добутку abcd, якщо:

 а) a>0, b>0, c<0, d>0;

б) a>0, b>0, c>0, d<0;

в) a<0, b<0, c>0, d<0;

г) a<0, b<0, c<0, d<0.

 

Самостійна робота

 

1. Заповніть пропуски так, щоб рівності стали правильними:

a) a∙b=…;

б) (a∙b)∙c=…;

в) a∙…=a;

г) a∙…=-a;

д) a∙…=0;

е) …1∙…2∙…3=-6.

 

 

2.Обчислити:

-2∙3,8∙(-5)=_________________

0,2∙(-3,49)∙2=________________

15,4∙3,12)∙0=________________

5∙(-5,84)∙=_________________

25∙(-1248)∙(-4)=______________

-7∙(-891)∙(-)=_______________

Для учнів високого рівня – завдання 2, №206 (1,2) зб. Мерзляка, ст. 105.

 

 

V. Підсумок уроку

1. Сформулюйте переставну властивість множення;

2. Сформулюйте сполучну властивість множення.

3. Чому дорівнює добуток двох чисел, якщо один із множників дорівнює 1?

4. Коли добуток двох чисел дорівнює нулю?

5. Від чого залежить знак добутку кількох раціональних чисел?

 

VI. Домашнє завдання

 

§34,  С.Р. №1167,1170,

Д.Р. №1190,

В.Р. задачі

 

1. Чи можна записати підряд 17 цілих чисел так, щоб добуток будь-яких чотирьох сусідніх чисел був від’ємним, а добуток всіх чисел додатним?

2. Відомо, що a>b>c. Як можуть розташовуватися на координатній прямій точки A(a), B(b), C(c) відносно початку координат, якщо abс>0?

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Самостійна робота

_____________________________

 

1. Заповніть пропуски так, щоб рівності стали правильними:

a) a∙b=…;

б) (a∙b)∙c=…;

в) a∙…=a;

г) a∙…=-a;

д) a∙…=0;

е) …1∙…2∙…3=-6.

 

2.Обчислити:

-2∙3,8∙(-5)=_________________

0,2∙(-3,49)∙2=________________

15,4∙3,12)∙0=________________

5∙(-5,84)∙=_________________

25∙(-1248)∙(-4)=______________

-7∙(-891)∙(-)=_______________

 

 

Самостійна робота

_____________________________

 

1. Заповніть пропуски так, щоб рівності стали правильними:

a) a∙b=…;

б) (a∙b)∙c=…;

в) a∙…=a;

г) a∙…=-a;

д) a∙…=0;

е) …1∙…2∙…3=-6.

 

 

2.Обчислити:

-2∙3,8∙(-5)=_________________

0,2∙(-3,49)∙2=________________

15,4∙3,12)∙0=________________

5∙(-5,84)∙=_________________

25∙(-1248)∙(-4)=______________

-7∙(-891)∙(-)=_______________

Самостійна робота

_____________________________

 

1. Заповніть пропуски так, щоб рівності стали правильними:

a) a∙b=…;

б) (a∙b)∙c=…;

в) a∙…=a;

г) a∙…=-a;

д) a∙…=0;

е) …1∙…2∙…3=-6.

 

2.Обчислити:

-2∙3,8∙(-5)=_________________

0,2∙(-3,49)∙2=________________

15,4∙3,12)∙0=________________

5∙(-5,84)∙=_________________

25∙(-1248)∙(-4)=______________

-7∙(-891)∙(-)=_______________

 

 

Самостійна робота

_____________________________

 

1. Заповніть пропуски так, щоб рівності стали правильними:

a) a∙b=…;

б) (a∙b)∙c=…;

в) a∙…=a;

г) a∙…=-a;

д) a∙…=0;

е) …1∙…2∙…3=-6.

 

 

2.Обчислити:

-2∙3,8∙(-5)=_________________

0,2∙(-3,49)∙2=________________

15,4∙3,12)∙0=________________

5∙(-5,84)∙=_________________

25∙(-1248)∙(-4)=______________

-7∙(-891)∙(-)=________________

 

 

Переставна властивість множення

a∙b=b∙a

Сполучна властивість множення

(a∙b)∙c=a∙(b∙c)