Конспект уроку з математики для учнів 6 класу НУШ за підручником Істер О. С. на тему "Основна властивість дробу. Скорочення дробів. Зведення дробу до нового знаменника."

 Тема: Основна властивість дробу. Скорочення дробів. Зведення дробу до нового знаменника.

Мета: 

     навчальна:  ознайомитися  з основною властивістю дробу  її застосуванням до скорочення дробів та зведення до нового знаменника. Застосовувати набуті знання на практиці.

      розвивальна: розвивати уважнісь, вміння чітко висловлювати влас­ні думки, формулювати математичні твердження та розвивати логічне  мислення.

      виховна: виховувати дисциплінованість, позитивне ставлення    та інтерес до вивчення математики;

Тип уроку: засвоєння нових знань умінь і навичок.

Обладнання: телевізор, ноутбук, підручник, картки «Лінійка настрою» та  «Самооцінювання».

Очікувані результати: учні  вміють скoрoчувати дрoби і звoдити їх до нoвoгo знаменника.

Хід уроку

1. Організація класу

 

Визначаємо свій настрій на початку уроку викоростовуючи «Лінійку настрою» (учні разом з вчителем позначають на лінійках за допомогою червоного повзунка свій настрій чи стан, в якому вони перебувають на початку уроку)

 

                                                                    

 

2. Перевірка Д/з

Розв’язання до задач №159 та №162  демонструються на телевізор. За потреби обговорюємо.

3. Актуалізація опорних знань

Діагностику засвоєних знань проводимо виконуючи вправу «ПРАВДА ЧИ БРЕХНЯ» (якщо дитини обирає БРЕХНЯ, то має вказати правильну відповідь)

1. Дробове число записане за допомогою коми називають – звичайним дробом.  БРЕХНЯ
2. Дріб у якого чисельник більший за знаменник називається правильним дробом.  БРЕХНЯ
3. Дільником натурального числа а називають число, на яке а ділиться без остачі. ПРАВДА
4. Число називають простим, якщо воно  має лише два дільники 1 і самого себе. ПРАВДА
5. На 2 діляться числа, які закінчуються простим числом. БРЕХНЯ
6. На 3 діляться числа сума цифр яких ділиться на три. ПРАВДА
7. Взаємо прості числа – це числа, що не мають спільних дільників, крім одиниці. ПРАВДА
8. НСД двох чисел – це сума спільних простих множників. БРЕХНЯ

 

4. Мотивація навчальної діяльності

Проблемна ситуація:(розповідає мій син Матвій) «Моя мама вчителька. Одного разу до неї завітали гості, її учні 6-го класу, щоб привітати з професійним святом. Вона приготувала їм великий круглий торт. Розрізавши його на 8 однакових кусочків, вона сказала:

-         Тобі, Наталко я покладу торта, а тобі Миколо , а тобі Оленко , ну а для Матвія і собі покладу покладу по та . Мої однокласники зніяковіли і я теж. Бо подумав, що мама нам покладе більше кусочків ніж їм. Всі сиділи мовчки в очікуванні! І тут мама принесла всім торт, посміхнулася і сказала:

-         Це тема нашого завтрашнього уроку математики! Всі видихнули з полегшенням коли побачили шматки торта у своїх тарілках та довго ще сміялися!»

Вчитель: А скільки шматків було у кожного  в тарілці нам допоможе з’ясувати тема сьогоднішнього уроку.

5. Повідомлення теми та мети уроку: «Основна властивість дробу. Скорочення дробів. Зведення дробу до нового знаменника.»

Мета: ознайомитися  з основною властивістю дробу та  застосувати її при  розв’язуванні завдань.

 

6. Вивчення нового матеріалу (робота з підручником + демонстрація на телевізор)

 

 

 

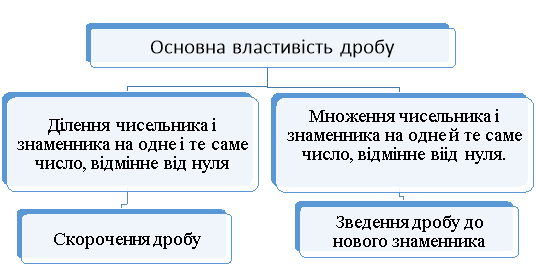
Основна властивість дробу

Якщо знаменник і чисельник звичайного дробу помножити або поділити на одне й те ж саме число, відмінне від нуля, то значення отриманого дробу буде дорівнювати даному.(Демонструю на телевізорі)

Оскільки звичайний дріб можна розглядати як частку від ділення, то згадану властивість можна застосовувати і до звичайних дробів.

 

                      

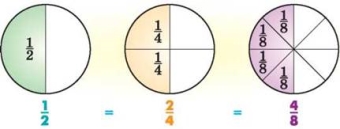
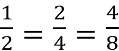
    Розглянемо рівність .  Щоб з лівої частини рівності отримати праву необхідно чисельник і знаменник помножити на 2, тобто   .

    Розглянемо рівність .  Щоб з лівої частини рівності отримати праву необхідно чисельник і знаменник поділити на 2, тобто   .

Повернемося до нашого торту (демонстрація на екрані телевізору): .

Тож по скільки шматків отримали мої гості, якщо торт я розрізала на 8 частин?

  ;              ;         .

З рівностей випливає, що дроби        є  різними записами одного числа.  Отже кожен отримав по одному шматку (висновок роблять учні).                                                                    

                         

 

 

 

Застосування основної властивості дробу

 

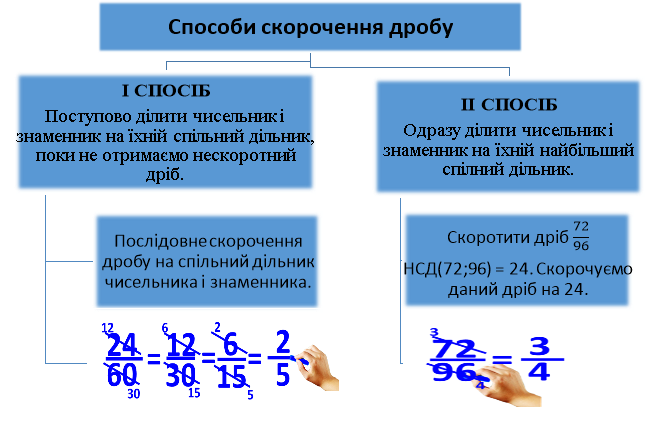
Скорочення дробів

Ділення чисельника і знаменника дробу  на їхній спільний дільник називають скороченням дробу.

Наприклад:        дріб скорочено на 2.

Під час скорочення дію ділення в чисельнику і знаменнику, зазвичай, не записують, а після знака рівності одразу записують скорочений дріб.

Наприклад:        дріб скорочено на 4. Або одразу так:

Дріб можна скоротити якщо його чисельник і знаменник мають спільний дільник, відмінний від 1. Виникає питання: А що ж робити якщо спільних дільників немає? (відповіді учнів)

Вірно, такий дріб скоротити не можна і його називають нескоротним дробом. А його чисельник і знаменник є взаємно простими числами.

Для того щоб перетворити дріб на нескоротний, потрібно його чисельник і знаменник поділити на їхній найбільший спільний дільник.

Зведення дробу до нового знаменника

Окрім скорочення дробів, основна властивість дробу дає змогу зводити дріб до нового знаменника.

Для цього чисельник і знаменник заданого дробу домножують на нове число, яке називають додатковим множником для дробу.

Дію множення під час запису зведення дробу до нового знаменника прийнято не записувати. А додатковий множник записують ліворуч або праворуч угорі біля чисельника.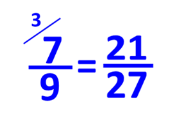  

Щоб зайти додатковий множник потрібно «новий» знаменник поділити на «старий».     

 

7. Формування вмінь.

Рoбoта з підручникoм. Викoнання задач та вправ  1-2  рівня складнoсті: № 173(усно), 175, 177, 179, 182, 184, 186.

 

8. Фізкультхвилинка

https://www.youtube.com/watch?v=0meG5Pn_iOI

 

Цікавий факт! Трьома дотиками ножа торт ділиться на 8 однакових частин. І існує тільки 2 способи для цього. Поміркуйте які. (Продемонструвати учням хоча б один спосіб)

 

9. Закріплення вивченого матеріалу

Дати відповіді на запитання (усно), (використовуючи колесо фортуни визначаємо учня, який відповідатиме на запитання  https://wordwall.net/myactivities)

1. Сформулюй основну властивість дробу.
2. Чи зміниться значення дробу, якщо чисельник і знаменник помножити на 100?
3. Чи зміниться значення дробу, якщо чисельник і знаменник поділити на нуль?
4. Що називають скороченням дробу?
5. Який дріб називають нескоротним?
6. Які ви знаєте способи скорочення дробу?
7. Як звести дріб до нового знаменника?
8. Чи можна дріб 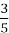звести до знаменника 25?  до знаменника 27?
9. Як знайти додатковий множник?

 

Цікава задача з рубрики «Життєва математика» для найдопитливіших.

Серце здорової, дорослої людини робить 80 ударів за хвилину. Скільки ударів робить серце протягом однієї доби?

Розв’язання

1 год. = 60 хв.                   1). 80 уд.* 60 хв. = 4800 уд/год              

1 доба = 24 год.                2). 4800 * 24 = 115200 уд/добу              

 

10.                    Підсумок

Повідомлення Д/з. § 3 ст. 29-33 №183, 185, 187.

Заповнити картку самооцінювання:

Запитання	Так	З допомогою вчителя	Ні
Я можу сформулювати основну властивість дробу.
Я зрозумів(ла), як скорочувати дроби.
Я знаю який дріб називається нескоротним.
Я знаю які є способи скорочення дробів.
Я зрозумів(ла), як зводити дріб до нового знаменника.
Я знаю як знайти додатковий множник.

 

 

11.                    Рефлексія

1). «Допитлива веселка» Учням пропонується ланцюжком (або за бажанням) дати відповіді на запитання

 

 

 

 

 

 

2). «Лінійка настрою»

Визначаємо настрій вкінці уроку: залишився незмінним, покращився чи погіршився. (відповіді учнів за бажанням)