Конспекти уроків №1-№6 з алгебри на тему: "Числові нерівності"
Урок №1
Тема. Числові нерівності. Доведення числових нерівностей
Мета : вивчити поняття: «числової нерівності», «правильні і неправильні числові нерівності», «строгі і нестрогі числові нерівності»; ознайомити з методом різниці, вивчити алгоритм порівняння чисел методом різниці;
розвивати логічне мислення, пам'ять, обчислювальні навички;
виховувати цілеспрямованість, працелюбність, упевненість у власних силах,культуру математичного мовлення , любов до точних наук.
Очікувані результати:
учні повинні знати: означення числової нерівності, правильних і неправильних, строгих і нестрогих числових нерівностей;
уміти застосовувати метод різниці до доведення нерівностей.
Обладнання: підручник, роздаткові матеріали.
Тип уроку: засвоєння нових знань.
Хід уроку:
І. Організаційна частина
Доброго дня!
Часто в народі говорять, як день розпочнеш, так і закінчиш, або: не з тієї ноги встав і інше. Бажаю вам всім розпочати наш урок з тієї ноги, з позитивом, щоб весь день та навчальний рік у вас пройшов у гарному настрої.
(Далі учитель ознайомлює учнів із підручником, особливостЯми вивчення алгебри в 9 класi; організаціЄю навчального процесу в 9 класi ( робИтЬ акцент на важливості серйозної пiдготовки до державної пiдсумкової атестації та ЗНО)
ІІ. Формулювання теми, мети й завдань уроку; мотивація навчальної діяльності
Для усвiдомлення учнями необхiдностi вивчення основного питання уроку (означення, що виражає залежнiсть мiж вiдношеннями «бiльше», «менше», «дорiвнює» й знаком рiзницi лiвої таправої частин нерiвностi) пропонуємо виконати такі завдання:
1) Який iз записiв: 0,25 > 0,117; 32 < 54; 0,5 > 1,4 – 0,9 зайвий? Чому?
2) Який iз записiв: 25 > 17; 0,32 < 0,4; 0,5 < 1,4 – 0,9 зайвий? Чому?
Пiд час обговорення результатiв виконання завдання пiдводимо
учнiв до висновку про те, що в 7 класi було вивчено питання про види, властивостi й способи перетворення виразiв, якi не мiстять дiлення на змiнну (цiлi вирази); у 8 класi вивчалися види, властивостi й способи перетворень виразiв, якi мiстять дiлення на змiнну(дробовi вирази). Отже, в 9 класi виникає необхiднiсть узагальнити
знання про види виразiв та логiчний зв’язок мiж ними. Це i є основною дидактичною метою вивчення роздiлу «Нерiвностi».
Фронтальна бесіда
Розглянемо задачу
На придбання м’ячів для спортклубу заплановано виділити 3000 грн. Визначте, яку найбільшу кількість м’ячів можна закупити на цю суму, якщо ціна одного м’яча становить 220 грн.
Розв’язання
Створимо математичну модель задачі. Якщо позначити кількість м’ячів через n, то їх вартість становитиме 220⋅n грн.
Щоб сума коштів на закупівлю м’ячів була меншою ніж 3000 грн., має виконуватись умова: 220⋅n < 3000.
Кількість м’ячів є натуральним числом. Найбільшим натуральним значенням n, яке задовольняє умову 220⋅n < 3000, є n =13. Отже, на виділені кошти можна придбати 13 м’ячів.
Запис 220⋅n < 3000 відрізняється від відомого вам запису 220⋅n = 3000 тим, що замість знака «=» використано знак «<».
ІІІ. Сприйняття та усвідомлення нового матеріалу
Два вирази, які з’єднані між собою знаками «>», «<», «≤»,«≥», називають нерівностями.
Нерівності, у яких обидві частини є числовими виразами, називають числовими нерівностями.
Числові нерівності бувають:
- правильними (істинними), наприклад: 14 > 2 4; - 3 > - 14 ; 
> 
;
< 3
- неправильними (хибними), наприклад: 18 > 24; - 13 > - 4 ; 
< 
;
> 11
Укажіть серед наведених числових нерівностей правильні:
16<45; -36>-2; 67>-160; -27>-2.
Історична довідка
Знаки відношень першими почали використовувати англійські математики:
знаки«>»і«<»—Томас Гарріот (1560–1621); знак«=»—Роберт Рекорд (бл.1510–1587). Окрім знаків нерівностей,вам відомий знак « ≠ » (не дорівнює). Запис a ≠ b означає, що a <b або a >b
Ви вже вмієте порівнювати між собою натуральні числа, цілі числа, десяткові дроби (тобто дійсні числа), використовуючи певні правила. Сьогодні ви познайомитеся з методом порівняння чисел і виразів, який має назву метод різниці.
Розглянемо приклади, наведені в таблиці. Для кожної правильної нерівності та рівності знайдемо різницю чисел, розташованих у лівій і правій частинах, та порівняємо цю різницю з нулем.
|
Нерівність або рівність
|
Різниця лівої і правої частин
|
Порівняння різниці з нулем
|
|
16 > 5 |
16 – 5 = 11 |
11 > 0, різниця чисел більша за нуль |
|
14>22 |
14 – 22= - 8 |
- 8<0, різниця чисел менша від нуля
|
|
14=14 |
14-14=0 |
0= 0 , різниця чисел дорівнює нулю
|
Чи помітили ви залежність між значенням шуканої різниці та знаками «>», «< », «=»?
Залежно від знака різниці роблять висновок про результат порівняння чисел.
Означення. Число a більше за число b, якщо різниця a-b є додатним числом. Число a менше від числа b, якщо різниця a - b є від’ємним числом, тобто
Якщо a > b, то a − b> 0, і навпаки, якщо a − b> 0, то a > b.
Якщо a < b, то a − b< 0, і навпаки, якщо a −b < 0, то a< b .
Якщо a = b, то a− b = 0, і навпаки, якщо a − b= 0, то a = b.
Для порівняння двох чисел a і b досить утворити різницю a – b і з’ясувати, яким числом вона є: додатним, від’ємним чи нулем. Такий метод порівняння називають методом різниці.
Розглянемо координатні прямі
а b x
b а x
порівняємо а та b.
Учні приходять до висновку, що кожному числу відповідає деяка точка координатної (числової) прямої, причому більшому числу відповідає точка, розташована праворуч від точки, яка відповідає меншому числу
Усне розв’язання
І група ІІ група
1.Порівняйте числа а і b, якщо: 1. Порівняйте значення виразів 4 x −1 і 3 x +1 ,
1) a− b = 2 7, ; 2) a − b= − 3 ; якщо: 1) x = 0; 2) x = 4; 3) x = -1 5 ; 4) x = 3 5 3) a = b +2 3 ; 4) 3+ b = 1+ a .
2 . Запишіть всі нерівності між числами, 2. Дано числа a, b, c, d, e. Відомо, що d< c ,
зображеними на числовій прямій a >c , b >e , e> a .
Зобразіть на числовій прямій задані числа.
Запишіть задані числа в порядку:
а с т а) зростання; б) спадання.
Нерівності бувають строгими і нестрогими:
знаки «>» і «<» є знаками строгих нерівностей ;
знаки «≥» і «≤ » є знаками нестрогих нерівностей ;
У ході вивчення математики постає питання доведення правильності нерівностей (часто кажуть «доведення нерівностей»). Існують різні методи доведення: геометричної інтерпретації, доведення «від супротивного», використання раніше доведених нерівностей тощо. Одним із найпоширеніших є метод різниці.
Приклад 1. Доведіть нерівність (а+3)(а+1)>а (а+4)
Розвязання: Утворимо різницю лівої та правої частин нерівності й спростимо її.
(а+3)(а+1)-а (а+4)=
+а+3а+3--4а=3
Проаналізуємо знак результату. 3 >0 .Оскільки різниця додатна, то ліва частина нерівності більша за праву, тобто (а+3)(а+1)>а (а+4).
Приклад 2. Доведіть нерівність 
, якщо a і b — невід’ємні дійсні числа. Доведення
Запишемо різницю лівої та правої частин нерівності 
=
=
≥ 0, якщо a ≥ 0, b ≥ 0 тому, що вираз 
різниця додатна, отже, ліва ча стина нерівності не менша від правої.
Вираз √ab називають середнім геометричним двох чисел а і b
Нерівність 
для a 
0, b 0 має спеціальну назву — нерівність Коші для двох чисел (на честь відомого французького математика Огюстена Луї Коші)
(Історична довідка. Огюстен Луї Коші (1789-1857)
Огюстен Луї Коші був сином високопоставленого французького муніципального службовця Луї-Франсуа Коші і його дружини Марі-Мадлен Дезестре.
Коші є автором низки значущих наукових робіт з математики: «Зібрання праць Огюстена Коші, опубліковане під науковим керівництвом Французької академії наук і під патронатом пана міністра народної просвіти» у 27 томах, «Підручник з аналізу для Королівської політехнічної школи», і т. д.
Жоден математик - за винятком хіба що Леонарда Ейлера - не залишив після себе стільки наукових праць, як Огюстен Коші).
(На першому поверсі Ейфелевої вежі розміщений список 72 найвідоміших французьких учених таінженерів XVIII–XIXст. Серед імен на південно-східній стороні вежі викарбовано ім’я Огюстена Луї Коші.)
IV. Осмислення нового матеріалу
(підручник автори: Мерзляк А.Г., Полонський В.Б., Якір М.С. 2017 рік. )
І група №1.4, №1.5, №1.8(2,3)
ІІ група №1.11(1,3)
№ 1.13(1), №1.16, №1.28(1)
V. Підсумок уроку
1.Повторення основних понять та означень, вивчених на уроці.
2.Висновок про виконану на уроці роботу та досягнення мети уроку.
3.Оцінювання роботи учнів на уроці.
VI.Домашнє завдання
Опрацювати п.1.
Виконати:
І група №1.3, №1.9, (1-3);
ІІ група № 1.12(1,2), №1.17 №1.29(1).
Урок №2
Тема. Розв’язування вправ
Мета : формувати вміння відтворювати зміст вивчених понять та застосовувати їх для виконання завдань на порівняння числових та буквених виразів, удосконалювати навички та вміння доводити числові нерівності;
розвивати логічне мислення, пам'ять, обчислювальні навички; вміння аналізувати та робити висновки;
виховувати дисциплінованість, працелюбність, упевненість у власних силах, культуру математичного мовлення, любов до точних наук.
Обладнання: підручник, роздаткові матеріали.
Тип уроку: удосконалення вмінь і навичок.
Хід уроку:
Найважливіше — не те велике,
до чого додумалися інші,
а те маленьке,
до чого дійшов ти сам.
Харукі Муракамі
І. Організаційна частина
«Психологічна настанова».
- Усміхніться один одному, подумки побажайте успіхів на цілий день. Для того, щоб впоратися на уроці із завданнями, будьте старанними і слухняними. Завдання наші такі:
Не просто слухати, а чути.
Не просто дивитися, а бачити.
Не просто відповідати, а міркувати.
Дружно і плідно працювати.
(Робота з епіграфом. Прочитайте епіграф. Як ви розумієте ці слова? (Відповіді учнів.))
ІІ. Перевірка домашнього завдання
Правильність виконання вправ домашньої роботи перевіряється в учнів,які потребують додаткові педагогічної уваги (зібрати зошити). Фронтальну перевірку якості виконання домашньої роботи можна провести у формі завдання «Знайди помилку».
(Знайди помилку
- Якщо m −k = −2 то m> k; Якщо k −m = 33 то m> k ; Якщо m < k то k − m= 0.
- Доведіть нерівність: 46а-71≤9а2+64а-107
Розглянемо різницю 46а-71-(9а2+64а-107)=46а-71-9а2-64а-107=-9а2-18а-178≤0.
- Порівняйте суму квадратів двох додатних чисел і квадрат їхньої суми.
а2 + в2 ≥ (а+в)2)
ІІІ. Актуалізація опорних знань
Усні вправи та повторення необхідного теоретичного матеріалу.
- Порівняйте значення виразів а(а+в) і ав.
А) а(а+в) ≥ ав Б) а(а+в) > ав В)а(а+в) < ав Г) а(а+в) ≤ ав
(Що називається нерівністю? Що означає «довести нерівність»? В чому заключається метод різниці доведення нерівностей?).
2. Знайдіть усі цілі числа x, для яких є правильною нерівність:
1) 4≤х<8 ; 2) -5 ≤х<4; 3) -14<2х<-4; 4) 8<2х<15; 5) 1<
<4; 6) -6 <
<10.
(Які нерівності називаються строгими?....-нестрогими?)
3. Подайте у вигляді квадрата двочлена вираз:
1) у2 – 2у + 1; 2) а2 + 12а + 36; 3) а2 – 8а+ 16; 4) а2 –ав +в2 –ав;
5) у-2
(х > 0; у > 0).
(Сформулюйте правила піднесення до квадрата суми та різниці двох виразів)
3. Порівняйте з нулем значення виразу:
1) в2; 2) в2 + 1; 3) (в + 1)2.
(Закінчіть речення: «квадрат будь-якого числа завжди…»
ІV. Мотивація навчальної діяльності
Виконуючи домашнє завдання ви зрозуміли, що процес доведення числових нерівностей є зовсім не простим. Тому ,щоб виконувати такі завдання без проблем, треба ще багато працювати, щоб накопичити необхідний досвід. Над цим і попрацюємо на сьогоднішньому уроці.
V. Удосконалення навичок
- Доведіть нерівність, якщо m — довільне дійсне число:
1) m (m−4) ≥ - 4 ; 2) n(n+6)+9 ≥0;
3) (m −3) ( m +5) > m (m+2) −1 7;
4) ( 4−m) (m+ 4) < (2 m −1) (m+ 3) − 3 m2− 5 m + 40 ;
- Доведіть нерівність: 1) а2+в2- 4а+10в+29 ≥ 0;
- Cвітланка має подарунковий сертифікат вартістю 300 грн для придбання солодощів. 1) Яку найбільшу кількість шоколадок за ціною 28 грн може купити дівчинка? 2) Чи можна за цей сертифікат придбати 27 круасан, якщо ціна одного круасана на 60 % менша, ніж ціна однієї шоколодки?
- Яка з рівностей є правильною — перша чи друга?
-
|4-
| = 
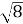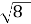- 4 2) |4- 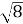| = 4-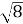
- Виконати № 1.15; №1.22; №1.24
VІ. Підсумок уроку
1. Висновок про виконану на уроці роботу та досягнення мети уроку
2. Вправа «Сходинка успіху»
Учні повинні самостійно визначити, на якій сходинці вони опинились в кінці уроку, і намалювати на ній фігурку людини.
Якщо ви уважно слухали, але нічого не робили, то ви, ймовірніше всього, опинились на сходинці під №1.
Якщо ви уважно слухали і виконували деякі вправи, то ви, ймовірніше всього, опинились на сходинці під №2.
Якщо ви уважно слухали і виконували усі вправи, але вони не завжди були правильно виконані, то ви, ймовірніше всього, опинились на сходинці під №3.
Якщо ви уважно слухали і виконували правильно усі вправи, то ви, ймовірніше всього, опинились на сходинці під №4
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
3 |
4 |
|
За результатами вправи проводиться коротке обговорення, чому саме на тій чи іншій сходинці намалювали себе учні, і що треба зробити для того, щоб у подальшому у навчанні піднятись на сходинку вище.
3.Оцінювання роботи учнів на уроці.
VIІ. Домашнє завдання
Повторити п.1, виконати №1.14; №1.29(2,3); №1.27*
Урок №3
Тема. Основні властивості числових нерівностей
Мета : вивчити властивості числових нерівностей; формувати вміння та навички застосовувати властивості числових нерівностей до розв’язування задач; розвивати логічне мислення, пам'ять, обчислювальні навички,вміння виділяти головне, аналізувати та робити висновки; виховувати працелюбність, наполегливість, цілеспрямованість, культуру математичних записів, впевненість у власних силах.
Очікувані результати: учні повинні знати і вміти доводити основні властивості нерівностей, застосовувати їх до розв’язування задач, зокрема до оцінювання значень виразів.
Обладнання: підручник, роздаткові матеріали.
Тип уроку: засвоєння нових знань та формування вмінь і навичок.
Хід уроку:
І. Організаційна частина
Якщо людина помістить всі свої знання в коло, то за колом вздовж його периметра залишається все те, що треба пізнати.
І якщо людина збільшує своє коло знань, вона починає розуміти, що не знає вона ще більше.
Давайте спочатку з’ясуємо, яким є ваше коло знань.
ІІ. Перевірка домашнього завдання
ІІІ. Актуалізація опорних знань
Усні вправи
1. Порівняйте числа х і у, якщо різниця у – х дорівнює: 1) 4; 2) -8; 3) 0.
(Як можна порівняти два числа? Сформулюйте правило різниці .Які нерівності називаються строгими, а які нестрогими?)
2. Доведіть нерівність:
1) с+5
a– 13 > a – 14;
3) a2 + b2 ≥ 2ab;
4) b + 
, b > 0;
(Що означає «Довести нерівність»? Що ви знаєте про нерівність Коші?)
3. Чи є правильним твердження:
1) якщо а = b, то b = а;
2) якщо а = b, b = с, то а = с;
3) якщо а = b, то а – с = b – с;
4) якщо а = b, то а + с = b + с;
5) якщо а = b, то ас = bс;
6) якщо а= b, то 
= 
.
ІV.Мотивація навчальної діяльності
Нерівності, що містять змінні, мають свої розв’язки .
Для того,щоб знайти ці розв’язки, треба нерівність розв’язати. Щоб уміти розв’язати будь-яку нерівність, слід вивчити всі властивості нерівностей .
V. Сприйняття та усвідомлення нового матеріалу
Розглянемо задачу.
Вхідний квиток до музею коштує 40 грн, а квиток на кожну окрему виставку в музеї — 3,5 грн. Суму, витрачену на відвідування музею, можна розрахувати за допомогою виразу A n = 3, 5⋅ n +40 грн, де n — кількість квитків на окремі виставки. Скільки виставок можна відвідати, якщо витрати не повинні перевищувати 65 грн? Коментар до розв’язання. За умовою An
65. Отже, необхідно знайти таке ціле число n, що задовольнятиме нерівність 3, 5⋅ n +40≤ 65. Для цього слід знати правила, за допомогою яких можна перетворювати числові нерівності, це те що ми не знаємо. Пригадайте властивості рівнянь і виконайте завдання.
Дано нерівність − 5< 6.
Користуючись прикладами (а–г), з’ясуйте, чи зміниться знак нерівності, якщо: 1) до обох частин нерівності додати (від обох частин нерівності відняти) одне й те саме число;
2) обидві частини нерівності помножити (поділити) на одне й те саме додатне число; від’ємне число. а) −5 + 3? 6 + 3; в) − 5⋅ 3? 6 ⋅ 3; б) −5 − 3? 6 − 3 ; г) − 5 ⋅ (−3) ?6 ⋅(- 3 )
Ви вже вмієте розв’язувати рівняння, використовуючи їх основні властивості.
Сьогодні ви познайомитеся з основними властивостями числових нерівностей, що допоможе вам розв’язувати задачі, математичними моделями яких є нерівності. Розглянемо основні теореми, які виражають властивості числових нерівностей, і з’ясуємо, чим властивості нерівностей схожі на властивості рівнянь, а чим відрізняються від них
Теорема 1. Якщо a> b , то b < a або якщо a <b , то b >a
Доведення 1) Доведемо перше твердження теореми: якщо a> b , то b< a . Застосуємо метод різниці. Якщо a> b , то різниця a −b є додатним числом, тоді різниця b −a = − ( a − b) є від’ємним числом, отже, b< a . 2) Аналогічно доводять друге твердження теореми: якщо a <b , то b >a .
ПОМІРКУЙТЕ! Які слова пропущено?
1) Якщо А дешевше від В, то В __________ А.
2) Якщо А важче за В, то В __________ А.
3) Якщо А вище за В, то В __________ А
Теорема 2. Якщо a < b і b< c , то a <c
Доведення Доведемо, що якщо a <b і b <c , то a <c . Застосуємо метод різниці: щоб довести, що a < c, досить довести, що a − c< 0. Запишемо різницю чисел a і c та перетворимо її: ac a− c= (a− c )+ b −b = (а −b) + (b −с ) . Оскільки за умовою a <b і b< c , то відповідно a − b< 0 і b− c < 0, тобто числа a− b і b −c є від’ємними. Отже, число a− c теж від’ємне (як сума від’ємних чисел a − bі b −c ). Звідси випливає, що a <c . Аналогічно доводять і таку властивість: якщо a >b і b >c , то a >c .
Якщо нерівності a <b і b< c правильні, то їх можна записати у вигляді подвійної нерівності a< b < c.
Розглянемо приклади.
5 < x, x < 9 . 5< x < 9 (x більше за 5 і менше від 9)
5 ≤ x, x < 9. 5 
9 (не менше від 5 і менше від 9)
5 < x, x≤ 9. 5< x ≤ 9 (x більше за 5 і не більше за 9 )
5 ≤ x, x ≤ 9. 5≤ x ≤ 9 (x не менше від 5 і не більше за 9)
Завдання . Запишіть у вигляді подвійної нерівності співвідношення:
1) x <21 і x > 0; 2) x <5 і x ≥ −4;
Теорема 3. 1) Якщо a> b і c — будь- яке число, то a+ c >b+ c.
- Якщо a > bі c — будь- яке число, то a− c > b − c.
Доведення 1) Доведемо, що якщо a> b і c — будь-яке число, то a+ c >b+ c. Застосуємо метод різниці. Утворимо різницю (a +c) − ( b+ с ). Маємо: (a+ c) − (b +c) = a− b. Оскільки за умовою a >b , то різниця a −b є додатним числом. Звідси випливає, що a+ c >b+ c.
2) Дію віднімання можна замінити дією додавання: a −c = a + (−c). Отже, можна зробити висновок: якщо a > bі c — будь-яке число, то a− c > b− c . Аналогічно доводять і таку властивість: якщо a < bі c — будь-яке число, то a + c< b+ c , a −c < b− c .
Для перетворення нерівностей використовують правило.
Правило 1 Будь-який доданок можна перенести з однієї частини правильної нерівності в іншу, змінивши знак доданка на протилежний.
Наприклад: 1) x + 4 > 11; x > 11− 4; x > 7 ;
2) x – 7 > 13; x > 13 +7; x > 20.
Завдання. 1. Додайте до обох частин нерівності:
1) − 17+ x < 12 число 17; 2) x + 8 ≥ 13 число –8.
2) Відніміть від обох частин нерівності:
15+ x ≤ 5 число 15; 2) 23− x < −11 число –23.
3) Перенесіть доданки зі змінною в ліву частину, а числа — у праву частину нерівності:
1) 24+ x 
‑ 4 x − 16; 2) − 13 − x ≥ 34 − 41 x.
Теорема 4. 1)Якщо a> b і c —додатне число,то a ⋅c > b⋅ c .
2)Якщо a>b і c—від’ємне число,то a⋅ c < b⋅ c
Доведення Нехай a > b. Помножимо обидві частини нерівності на число с і застосуємо метод різниці. Запишемо різницю та перетворимо її: a ⋅c − b c =− c( a−b) За умовою a >b , отже, різниця a −b є додатним числом. 1) Якщо c > 0, то добуток c (a −b ) є додатним числом, тобто різниця a⋅ c −b⋅ c є додатним числом, отже, a ⋅c > b⋅ c . 2) Якщо c < 0, то добуток c (a −b) є від’ємним числом, тобто різниця a⋅ c −b⋅ c є від’ємним числом, отже, a ⋅ c< b⋅ c . Дію ділення можна замінити дією множення: a : с = a 
. Отже, доведені властивості справедливі й для випадку ділення обох частин нерівності на деяке число, відмінне від нуля. Аналогічно доводять і такі властивості: якщо a <b і c — додатне число, то ac < bc; якщо a < bі c — від’ємне число, то ac > bc
Правило 2 Обидві частини нерівності можна помножити (або поділити) на одне й те саме додатне число. При цьому знак нерівності не змінюється. Обидві частини нерівності можна помножити (або поділити) на одне й те саме від’ємне число. При цьому знак нерівності змінюється на протилежний.
Завдання Виконайте множення або ділення обох частин нерівності від- повідно до запису:
1) 0,5x < 48( ⋅4); 2) − x ≥13 (⋅ (−1)) ; 3) 32 x <- 64
Наслідок із теореми 4. Якщо обидві частини правильної нерівності, які є числами одного знака, замінити оберненими до них числами і змінити знак нерівності на протилежний,то отримаємо правильну нерівність.
Якщо ab > 0 і a > b, то 
Завдання 1 . Відомо, що 2 < m< 7. Оцініть значення виразу:
1) 6m; 2) −m; 3) 2−m;
Завдання 2. Відомо, що сторона a ділянки квадратної форми набуває значень 4 < a <7 (у м). Оцініть периметр (у м) ділянки квадратної форми зі стороною, втричі більшою за a.
VІ. Осмислення нового матеріалу
(підручник автори: Мерзляк А.Г., Полонський В.Б., Якір М.С. 2017 рік. )
І група №2.1, №2.3, №2.7, №2.10
ІІ група №2.5, № 2.9, №2.12, №2.15, №2.19
Ігровий пошук «Вірю — не вірю»
Діти, зараз я пропоную прослухати вам речення і погодитися з моїм твердженням чи його спростувати.
1) Якщо a < −3, то − a > 3.
2) Якщо x >5, то x >2 .
3) Якщо y < −2, то y < −4.
4) Якщо один автобус може перевозити не більше 20 пасажирів, то 3 таких автобуси
можуть перевезти 58 пасажирів.
5) Якщо в книгарні ціна будь-якої однієї книжки не менша ніж 30 грн, то 5 книжок
можуть коштувати 140 грн.
VІІ. Підсумок уроку
Рефлексія. Продовжте речення:
1) Сьогодні на уроці я дізнався….
2) Мені сподобалось….
3) Сьогодні на уроці я навчився…
4) На мою думку можна було б…
5) Тепер я знаю, що…
Вчитель: Ми вивчили основні властивості числових нерівностей,але попереду іще багато невідомого нас чекає в загадковій країні «Алгебра». На наступних уроках ми обов’язково над цим будемо працювати.
(Оцінювання роботи учнів на уроці)
VIІІ. Домашнє завдання
Опрацювати п.2, виконати:
І група №2.4, №2.6;
ІІ група № 2.8, №2.11 №2.20*
Урок №4
Тема. Додавання і множення числових нерівностей. Оцінювання значення виразу
Мета : домогтися засвоєння учнями змісту поняття «додати нерівності почленно» та «перемножити нерівності почленно», а також змісту властивостей числових нерівностей, що виражені теоремами про почленне додавання і почленне множення числових нерівностей і наслідків із них. Виробити вміння відтворювати названі властивості числових нерівностей та використовувати ці властивості для оцінювання значення виразів, а також продовжити роботу з відпрацювання навичок доведення нерівностей, порівняння виразів із використанням означення та властивостей числових нерівностей; розвивати обчислювальні навички, вміння логічно мислити, аналізувати, робити висновки, виховувати наполегливість, самостійність, цілеспрямованість, культуру математичного мовлення та математичних записів, віру у власні сили.
Обладнання: підручник, роздаткові матеріали
Тип уроку: засвоєння знань, формування первинних умінь.
Хід уроку:
І. Організаційна частина
ІІ. Перевірка домашнього завдання
ІІІ. Формулювання мети і завдань уроку.
Мотивація навчальної діяльності учнів
Кіностудія знімає серіал із x серій, 19 ≤ x ≤ 24. Кожна серія триває y хв,
30 ≤ y ≤ 40. Як оцінити загальний час показу всього серіалу (у хв), якщо транслювати його без перерви й реклами?
Коментар до розв’язання. Щоб знайти загальний час показу серіалу, необхідно тривалість однієї серії помножити на кількість серій. Оскільки в умові подано не конкретні значення x і y, а межі, у яких вони містяться, то для розв’язання задачі слід перемножити дві нерівності. Виникає питання: як у цьому випадку знайти значення добутку x · y?
ІV. Сприйняття та усвідомлення нового матеріалу
Існують правила, за якими можна виконувати окремі арифметичні дії з нерівностями. Розглянемо відповідні теореми, які для зручності будемо доводити для строгих нерівностей, але ці теореми справедливі також у випадку нестрогих нерівностей
|
1.Теорема (властивість) про почленне додавання числових нерівностей |
|||||
|
Якщо а > b і c > d, то a + c > b + d. (Якщо a < b і c <d ,то a +c < b+ d) |
|||||
|
Доведення 1) Розглянемо різницю (a +c) − (b +d) і перетворимо її: (a+ c) − (b +d) = a +c −b− d = (a− b) + (c− d). За умовою a > b і c >d, тоді a − b > 0 і c −d > 0, таким чином, (a −b) + (c− d) > 0.
Нерівності a >b і c >d (або a <b і c< d ) називають нерівностями одного знака. Нерівності a> b і c <d (або a < bі c >d ) називають нерівностями протилежних знаків. Приклад. Виконайте додавання нерівностей:
1) a < 4 і с < 2; 2) x 3) x < − 16 і y <32 ; 4) -3<x<2 і 5<у<7 |
|||||
|
|||||
|
Якщо а> b>0 і c> d >0, то ac > bd. (Якщо0 < а< b і 0< c< d , то ac < bd) Доведення. 1) Розглянемо різницю ас-bd= ас-bc+bc-bd=c(a-b)+b(c-d).За умовою a-b>0, c-d>0, c>0,b>0. Отже, ac > bd. 2) Учні самостійно доводять друге твердження теореми для нерівностей 0 < а< b і 0< c< d Наслідок. Якщо 0 < а < b, то an < bn, де п — натуральне число. |
|||||
|
Приклад 1. Відомо, що 3 < а < 4; 2 < b < 3. Оцінимо значення виразу:
1) а + b; 2) а - b; 3) аb; 4) Розв'язання |
|||||
- 2 > -b > -3 -3 < -b < -2 0< а - b< 2
3) 6< аb<12, 4) 3 < а < 4
V. Осмислення нового матеріалу (підручник автори: Мерзляк А.Г., Полонський В.Б., Якір М.С. 2017 рік. ) №3.1; №3.3,№3.5; №3.8; №3.12; №3.16; №3.18;№3.25*.
VІ. Самостійна робота І варіант ІІ варіант 1. Відомо, що 6< m < 8 і 2 < n< 3. 5< m < 7 і 1 < n < 3.
Оцініть значення виразу m +n . А) 8 < m +n < 11 А) 8 < m +n < 9 Б) 9 < m+ n <10 Б) 6 < m+ n <10 В ) 12 < m+ n < 24 В) 5 < m+ n < 21 Г) 6 < m + n < 3 Г) 5 < m + n < 7 2. Відомо, що 0 <a <2 і 1 < b < 4. 2 <a <5 і 1 < b < 3 Оцініть значення виразу a− b . А) -2 < a− b < -1 А) 1 < a− b < 2 Б) -4 < a− b <-1 Б) -1 < a− b <4 В ) 1 < a− b < 2 В) -1 < a− b < 2 Г) -1 < a− b < -2 Г) 3 < a− b < 8 3. Відомо, що 4 < p < 7. 1 < p < 5.
Оцініть значення виразу
А)
Б)
В ) 7 <
Г) 4 <
4.Відомо, що 4 < p < 10 і 2 < q < 6. 1 < p < 8 і 2 < q < 6. Оцініть значення виразу q p + 2 . А) 10 < q p + 2 < 62 А) 4 < q p + 2 < 20 Б) 8 < q p + 2 <22 Б) 4 < q p + 2 <50 В ) 6 < q p + 2 < 16 В) 3 < q p + 2 < 14 Г) -1 < q p + 2 < -2 Г) 3 < q p + 2 < 8 5. Майстер виготовляє дерев’яні декоративні дощечки прямокутної форми. Ширина такого прямокутника становить a см, 10 <a <20, довжина — b см, 15 < b <30. Оцініть площу S (у см2) цього Оцініть периметр P (у см) цього прямокутника. прямокутника. 6.Відомо, що 20< x <40, 1 < y < 20. 10< x <80, 2 < y < 10. Установіть відповідність між початком речення (1–3) та його закінченням (А–Г) так, щоб утворилося правильне твердження.
Г) більше за 1 і менше від 40.
VIІ. Домашнє завдання Повторити п.3, виконати №3.7; №3.15; №3.17; за бажанням№3.26 VIІІ. Підсумок уроку У майстерні виготовляють вітражні вікна прямокутної форми. Довжина й ширина кожного вікна дорівнюють a м і b м відповідно. Оцініть площу S (у м2) вікна, якщо за технічними умовами дозволено такі його розміри (у м): 0,6 < a < 1,4; 1, 4 < b < 2. (Висновок про виконану на уроці роботу та досягнення мети уроку. Оцінювання роботи учнів на уроці.)
|
|
2) а
|
|
|
|
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
|
|
|||||
Б ) більше за 20 і менше від 800.
. В) більше за 1/40 і менше від 3/2.
Урок №5
Тема. Розв’язування вправ
Мета : перевірити знання теорем про почленне додавання і множення нерівностей, удосконалити уміння застосовувати ці теореми до розв’язування задач оцінювання значень виразів; розвивати логічне мислення, пам'ять, обчислювальні навички, вміння аналізувати ситуацію, формувати інтерес до знань; виховувати наполегливість, зосередженість, уважність, працьовитість, цілеспрямованість.
Обладнання: мультимедійний проектор, презентація
Тип уроку: удосконалення умінь і навичок.
«Міцні знання – гарантія успіху»
Хід уроку
І. Організаційний момент
Доброго дня, дорогі діти. Сідайте, перш за все перевірте готовність робочих місць. Налаштуйтеся на серйозний лад, адже нам сьогодні потрібно буде плідно попрацювати. Не забудьте проявляти кмітливість, рішучість, впевненість у ході прийняття рішень.
ІІ. Мотивація навчальної діяльності учнів
1. Аутотренінг
А щоб налаштувати себе на активну роботу, проведемо аутотренінг. Прошу повторювати за мною:
Я – учень.
Я – особистість творча.
Я думаю, аналізую.
Я не боюся висловлювати свої думки
Помилившись, міркую далі.
На помилках вчаться
Я хочу багато знати.
Оголошення теми й мети уроку. Хочу звернути вашу увагу на епіграф нашого уроку: “Міцні знання – гарантія успіху”. Саме вони і допомагають людині стати успішною. Практика неможлива без теорії, давайте зараз згадаємо все те, що нам знадобиться сьогодні на уроці.
ІІІ. Перевірка домашнього завдання
ІV. Актуалізація опорних знань
Інтерактивна вправа «Мікрофон»
1. У якому разі число а вважають більшим за число в?
2. У якому разі число а вважають меншим від числа в?
3. Яке із чисел а або с –більше, якщо відомо, що а>в і в>с?
4. Сформулюйте теорему про додавання до обох частин нерівності одного й того
самого числа.
5.Сформулюйте теорему про множення обох частин нерівності на одне й те саме число.
6. Сформулюйте теорему про почленне додавання нерівностей.
7. Які нерівності називають нерівностями однакового знака, а які- нерівностями протилежних знаків?
8. Сформулюйте теорему про по членне множення нерівностей
V. Узагальнення та систематизація понять.
Інтерактивна вправа «Взнай слово»
Дано: 3< р <6, 0,6< с < 1. Знайдіть:
1) найбільше значення виразу рс 3) найбільше значення виразу 2р+с
2) найменше значення виразу рс 4) найбільше значення виразу 
5) найменше значення виразу р-с 6) найменше ціле значення виразу рс
7) найбільше значення виразу 2р-3с
|
Е |
Ж |
І |
Н |
Н |
Р |
Е |
|
10 |
13 |
6 |
2 |
1,8 |
10,2 |
1 |
Відповідь: Інженер
Майбутні інженери в галузі будівництва отримують необхідні знання для проектування, спорудження,експлуатації,реконструкції автодоріг, будівельних об’єктів,а також знання в галузі новітніх та енергозберігаючих технологій створення ефектив- них конструкцій і матеріалів для будівельно-монтажних робіт.
Розвяжемо задачу «БУДІВНИЦТВО АВТОЗАПРАВОК»
З міста A виходять три автомагістралі. Автозаправки B і C розташовані на автомагістралях 1 і 3 відповідно. На автомагістралі 2 заплановано розмістити автозаправку D і побудувати дорогу, що сполучить усі три автозаправки. Де необхідно розмістити автозаправку D, щоб нова дорога BDC мала найменшу довжину? Відповідь обґрунтуйте
В
D
А
С
VІ. Засвоєння провідних ідей і теорій на основі широкої систематизації.
Інтерактивна вправа «Вмій застосувати»
Розв’язування прикладних задач в групах
(Попередньо підготуйте рольові картки 6 малих груп, додаткову інформацію та список «ситуацій та подій». Об’єднайте учнів у групи. Роздайте рольові картки та попросіть їх «увійти» в роль, ознайомившись із інформацією. Вишикуйте учнів, які будуть презентувати ролі, вздовж лінії (уявної або намальованої на підлозі).
Розкажіть учасникам, що ви прочитаєте список ситуацій. Якщо вони на задану ситуацію можуть відповісти «так», то їм слід зробити крок вперед. В іншому випадку вони повинні залишатись на місці і не рухатись. Запропонуйте скористатися при розрахунках додатковою інформацією. Читайте поступово по одній ситуації. Робіть паузи між прочитаними ситуаціями так, щоб в учасників був час провести розрахунки, ступити вперед і оглянутись навколо та зрозуміти своє положення відносно інших учасників.)
Довідкова інформація
-Прожитковий мінімум в Україні з 1 січня 2020 року становить 2027 грн.
-Для дітей віком до 6 років - 1779 грн
-Для дітей віком від 6 до 18 років - 2218 грн
-Для працездатних осіб - 2102 грн
-Для осіб, які втратили працездатність-1638 грн
-Ставка податку на доходи фізичних осіб – 18%. Податок на доходи не нараховується на пенсії, стипендії,допомогу на дітей, допомогу по безробіттю, тощо.
- Платники податку, які утримують двох чи більшe дітей віком до 18 рoків, дитину-інваліда, мають право нaподаткову соціальну пільгу на кожну тaку дитину.
-Допомогу держави – субсидію – можуть отримати українські родини, якщо їхні комунальні витрати перевищують в середньому 15% щомісячного сукупного доходу.
-Малозабезпеченим сім’ям, які мають середньомісячний сукупний дохід нижчий від прожиткового мінімуму для сім’ї, призначається державна соціальна допомога.
|
Батько, мати, двоє дітей шкільного віку. Заробітна платня батька – 8000 грн. Заробітна платня матері – 5500 грн.
Щомісячні витрати – 11000 грн., з них оплата комунальних послуг – 2600 грн.
|
Батько,мати,дочка-студентка. Заробітна платня батька – 9000 грн. Заробітна платня матері – 4500 грн. Стипендія дочки 1600 грн.
Щомісячні витрати – 9000 грн., з них оплата кому- нальних послуг – 2300 грн.
|
Мати-одиначка, ди- тина дошкільного віку. Заробітна платня матері – 4200 грн.
Щомісячні витрати – 3200 грн., з них оплата кому- нальних послуг – 1700 грн
|
|
Батько з інвалідністю, мати, дитина дошкільного віку. Пенсія батька – 2000 грн. Заробітна платня матері – 4500 грн.
Щомісячні витрати – 5000 грн., з них оплата кому- нальних послуг – 700 грн.
|
Безробітній чоловік Допомога по безробіттю – 2500 грн.
Щомісячні витрати ≈ 2500 грн., з них оплата кому- нальних послуг – 900 грн.
|
Батько, мати, дитина 1 рік, бабуся-пенсіонерка Заробітна плата батька – 9000 грн. Щомісячна виплата на дитину до 3-х років – 860 грн. Пенсія бабусі – 1710 грн.
Щомісячні витрати – 9000 грн., з них оплата кому- нальних послуг – 1400 грн.
|
Приклади ситуацій
• Доходи родини перевищують прожитковий мінімум.
• Сім’я має право на отримання субсидії.
• Сума податку на доходи фізичних осіб, яку сплачують члени родини n відповідає умові: 1500 грн. < n <1800 грн.
• Один із працюючих членів родини може звернутися із заявою про надання податкової соціальної пільги.
• Протягом року родина може дозволити собі покупку побутової техніки вартістю х, яка відповідає умові: 2300 грн. < х < 14000 грн.
• Залишок коштів у місяці родина розмістила на депозит під 12% річних. Розмір прибутку родини, отриманого протягом року > 3500 грн.
Обговорення
1.Було легко чи важко грати різні ролі?
2.Якою ви уявляєте родину, чию роль презентували?
3. Чи були такі моменти, коли хтось відчував, що їхні фінансові можливості
обмежують задоволення певних потреб?
4.Яким чином такий дослід відображає суспільство?
5.Кому належить провідна роль у створенні рівних можливостей для громадян?
6.Які перші кроки можна зробити для усунення нерівності в суспільстві?
V. Домашнє завдання
Повторити п.1-3, завдання №1 (с.54); №3.28*
VI. Підсумок уроку
Пляшечка шампуню коштує 40 грн. Яку найбільшу кількість таких пляшечок можна
придбати на 170 грн під час дії акції, коли знижка на цей шампунь складає 25 %?
(Висновок про досягнення мети уроку та оцінювання роботи учнів на уроці)
Урок №6
Тема. Самостійна робота
Мета : перевірити рівень засвоєння учнями теми «Числові нерівності», а саме вміння : порівнювати числа, додавати і множити числові нерівності, оцінювати значення виразів, доводити нерівності; розвивати логічне мислення, пам'ять, вміння правильно і чітко висловлювати власні думки в письмовому вигляді; виховувати уважність, працьовитість, самостійність, відповідальність, дисциплінованість.
Обладнання: картки (два варіанти)
Тип уроку: контроль знань і вмінь.
Хід уроку
І. Організаційний момент
(привітання з учнями, перевірка готовності учнів до уроку, створення робочої атмосфери)
ІІ. Перевірка домашнього завдання
(Відповісти на можливі запитання учнів і зібрати зошити на перевірку
в кінці уроку)
ІІІ. Формулювання мети і завдань уроку
(Оголосити тему уроку, сформулювати разом з учнями мету й завдання уроку, налаштувати учнів на роботу, провести інструктаж щодо виконання завдань самостійної роботи, нагадати правила поведінки під час виконання самостійної роботи)
ІV. Самостійна робота
І варіант
1.Оцініть значення виразу 
, якщо − 21 < а < 3.
А) - 1< а< 7 Б) 7< а< 9 В) - 7< а< 1 Г) -7< а< 3
2. Оцініть значення виразу a +b , якщо 10 < a < 15 і 6< b <9.
А) 19< а+ b < 21 Б) 16< а+ b < 24 В) 4< а+ b < 9 Г) 15< а+ b <13
3. Укажіть нерівність, яка є правильною при всіх дійсних с.
А) 4с ≥ с Б) с - 1 ≥ с +1 В) 4(с- 1) ≥ 0 Г) (с-4)2 ≥ 0
4. Відомо, що 5< х < 8. Оцініть значення виразу 
А) 
< 
< 
Б) 
< < В ) 5 < < 8 Г) -8 < < -5
5. Укажіть число, яке є розв’язком нерівності – 2
x < 4 .
А) -3 Б) -1 В) 4 Г) 5
- Відомо, що 5< a < 7 і 6< b <8. Укажіть число, яке не може бути значенням виразу ab.
А)35 Б) 24 В) 48 Г) 55
7.Відомо, що −2 < x < 4 . Оцініть значення виразу 10 −4x.
А) -8<10 −4x <16 Б) -16<10 −4x <8 В) - 6< 10 −4x < 18 Г) -6<10 −4x < 16
8. Для закупівлі енергозберігальних ламп за ціною 50 грн планують виділити від 700 до 1100 грн.
1) Скільки таких ламп можна закупити на заплановану суму?
2) Яку найбільшу кількість таких ламп можна закупити на заплановану суму, якщо ціна однієї лампи збільшиться на 20 %?
9. Доведіть нерівність (а-6)2 > −а (12-а ), якщо а — довільне дійсне число.
10. Доведіть нерівність (1+а ) ( 1+ b) 4
для a 0, b0
ІІ варіант
1.Оцініть значення виразу -4х , якщо − 1 < х < 3.
А) - 3< -4х < 1 Б) -3 <-4х < 1 В) – 12 < -4х < 4 Г) -12<-4х < -4
2. Оцініть значення виразу х +у , якщо 2 < у < 5 і 5< х <8.
А) 10< х +у < 11 Б) 7< х +у < 13 В) 7< х +у < 12 Г) -7< х +у <13
3. Укажіть нерівність, яка є не правильною при всіх дійсних с.
А) 4с ≥ 0 Б) с - 1 с +1 В) 4(с- 1) ≥ 0 Г) (с-4)2 ≥ 0
4. Відомо, що 4 < у < 9. Оцініть значення виразу 
А) 
< 
< 
Б) 
< < В ) 4 < < 9 Г) -4 < < -9
5. Укажіть число, яке не є розв’язком нерівності – 
x 3 .
А) -3 Б) -1 В) 0 Г) 3
6.Відомо, що 4< х < 6 і 5< у <8. Укажіть число, яке не може бути значенням виразу ху.
А)25 Б) 33 В) 48 Г) 45
7.Відомо, що −2 < x < 4 . Оцініть значення виразу 12 −2x.
А) -8<12 −2x <4 Б) 16<12 −2x <20 В) 4< 12 −2x < 16 Г) -4<12 −2x < 16
8. Олена планує купити 12 зошитів у клітинку й 10 зошитів у лінійку. Ціна зошита в клітинку не перевищує 8 грн, у лінійку — 5 грн. Доведіть, що Олені на всю покупку вистачить 125 грн, ураховуючи, що дівчина скористається карткою магазина, яка надає право на знижку 15 %.
9. Доведіть нерівність (с-7)2 > −с (14-с ), якщо с — довільне дійсне число.
10. Доведіть нерівність (2+а ) ( 2+ b) 8 для a 0, b0
V. Домашнє завдання.
Повторити п.1-3
Опрацювати завдання, які викликали труднощі під час виконання самостійної роботи
VІ. Підсумки уроку.
(Зібрати роботи учнів, відповісти на можливі запитання)
про публікацію авторської розробки
Додати розробку