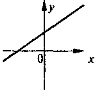
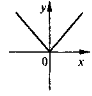
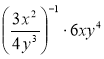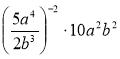Конспекти уроків алгебри 8 клас Розробка теми «Степінь з цілим показником»

Конспекти  уроків алгебри 8 клас

Розробка теми «Степінь з цілим показником»

Котис О.В., вчитель математики

Городницької ЗОШ І-ІІ ст.. Скалатської міської ради

Урок 23

Тема: Аналіз контрольної роботи. Степінь з цілим показником.

Мета. Домогтися засвоєння учнями змісту означення степеня з ці­лим від'ємним показником (для цілої та дробової основи степеня); сформувати вміння відтворювати означення степеня та застосовувати його для перетворення степеня з цілим від'ємним показником у дріб, та навпаки, сформувати вміння розв'язувати вправи на обчислення значень числових виразів із застосуванням вивченого означення степеня з цілим показником.

Тип уроку. Засвоєння знань та первинних умінь.

Обладнання. Підручник (О.С.Істер).

Хід уроку

I. Організаційний етап. Аналіз контрольної роботи

Учитель аналізує найбільш допущені помилки, та виправляє їх. На закріплення учні розв’язують приклади , в яких допущені помилки

III. Формулювання мети і завдань уроку

IV. Актуалізація опорних знань та вмінь

• Що називається степенем числа?
• Що означає , ,

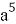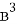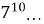
Виконання усних вправ

1. Прочитайте вираз, назвавши основу і показник степеня:

1) 5⁴;               2) (6,1)⁹;       3) 10¹;

4) (-8)⁵;      5) 0¹⁷;       6) .

2. Піднесіть до квадрата:

1) 4;          2) -3;         3)        4) ;          5)           6) 0,9.

3. Піднесіть до куба:

1) 3;          2) -2;         3) ;       4);        5);               6) -0,1.

4. Визначте знак виразу, не виконуючи піднесення до степеня:

1);            2);      3) ;            4)                     

 5) (-2)⁹                6) -2¹⁰              7) (-2)¹⁰;              8) -2⁹;               

5.Укажіть порядок дій в обчисленні значення виразів:

15² – 3⁴; 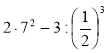; (3² – 2³)²⁰.

V. Засвоєння знань

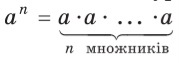Нагадаємо, що в 7 класі ми вивчали степінь з натуральним показником. За означенням степеня                                                             , якщо п > 1, п — натуральне число і а¹=а.

У математиці, а також під час розв'язування задач прак­тичного змісту, наприклад з фізики або хімії, трапляються степені, показник яких нуль або ціле від'ємне число. Степінь з від'ємним показником можна знайти в науковій та довідко­вій літературі. Наприклад, масу атома гелію, записують так: 6,6410^-27 кг. Як розуміти зміст запису 10^-27?

Розглянемо степені числа 3 з показниками 1, 2, 3, 4...:

У цьому рядку кожне наступне число у 3 рази більше за попереднє. Продовжимо рядок вліво, зменшуючи кожного разу показник степеня на 1. Дістанемо:

Число 3° повинно бути в 3 рази менше за 3¹=3. Але в 3 рази меншим за число 3 є число 1, отже, 3⁰ = 1. Така сама рівність а⁰ = 1 буде виконуватися для будь-якої основи а, відмінної від нуля.

Степінь числа а, яке не дорівнює нулю, з нульовим показником дорівнює одиниці:

Зліва у рядку від числа 3⁰ = 1 стоїть число 3^-1. Це число у 3 рази менше за 1, тобто дорівнює . Отже, . Міркуючи далі аналогічно, дістанемо

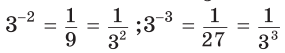
і т.д.  Доцільно прийняти наступне означення степеня з цілим від'ємним показником (-n):

 

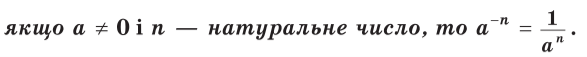
aⁿ=

 

Приклад 1. Замінити степінь з цілим від’ємним показником дробом:

Розв’язання:

 

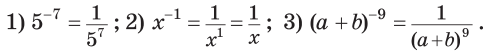
Приклад 2.  Замінити дріб степенем з цілим від’ємним показником:

Розв’язання:

Приклад 3. Виконати піднесення до степеня:  

Розв’язання:

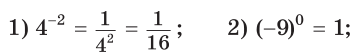
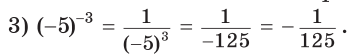
Розглянемо піднесення до від’ємного цілого степеня дробу . Якщо n - натуральне число і , маємо:

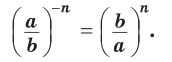
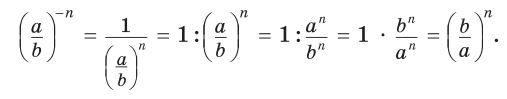
Отже,

 

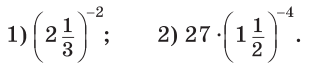
Приклад 4. Обчислити:  

Розв’язання:

 

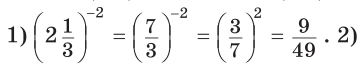
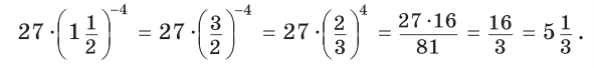
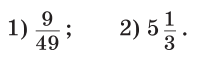
Відповідь:

 

Означення степеня з цілим від’ємним показником
1.Якщо:  ≠0,     n — натуральне число,   то	Приклад.     1) ;
2. Якщо:     ≠0,      n=0;    то  0=1	Приклади.1) (-2,6)0=1;     2)
3.  Записи    0 0,   0 -п     не мають змісту
4. Якщо: ;   n — натуральне число,   то   .	Приклад.
5.Обчисліть  значення виразу:	+9-2-(-2,6)0=
Крок1. Замінити степені з від'ємними показниками на степені з натуральними показниками:	=+ - (-2,6)0 =
Крок 2.     Виконати піднесення до степеня:	=+ - 1=
Крок 3.      Виконати дії з дробами:	2 – 1 + = 1

 

VI. Формування вмінь

Виконання усних вправ

1. Обчисліть: 2⁴; (-3)²; (0,1)³; (-1)⁸; 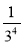; ; 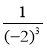(-15)⁹; 0,3⁰; 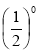; 0⁰.
2. Замініть дробом степінь із цілим від'ємним показником. Заповніть пропуски.

; ; ; .

3. Замініть дріб степенем із цілим від'ємним показником:

; ;  ; 

 

       Вчитель:  Діти, вам необхідно було самостійно попрацювати з додатковою літературою, відшукати історичні відомості про степінь з цілим від’ємним показником .

 

Метод  «Мікрофон»

Учень 1. Від’ємні показники степеня першим систематично почав вживати І. Ньютон, хоч вони були відомі раніше. У 1667 році він зазначив «як алгебраїсти замість аа, ааа і т.д. пишуть а², а³, і т.д. так я  замість , пишу, а^-2, а ^-3 »

 Учень 2. До нашого часу збереглися глиняні плитки з таблицями квадратів і кубів натуральних чисел, зроблені стародавніми вавилонянами. Згодом учені стали розглядати четвертий, п’ятий та вищі степені, називаючи їх спочатку квадрато – квадратом, кубо – квадратом і т.д.

Учень 3. Степінь з нульовим показником запровадили в V столітті незалежно один від одного самаркандець  Аль – Каші і француз Н. Шюке.

Учень  4. Француз Н. Шюке також використовував степені з від’ємними показниками.

            Учень 5. Теорію степенів з від’ємними показниками розробив у XVІІ столітті англійський математик Джорж  Валліс.

 

Виконання письмових вправ

№263, 264 , 266 усно

 

 

№268, 270, 272 письмово самостійно (робота в парах)

 

 

 

VII. Підсумки уроку

Тестові завдання (на картках)

     1.    Тотожно рівним виразу 7^-3 є вираз:

а)  -7³;             б)            в)               г) .

     2.    Тотожно рівним дробу    є вираз:

 а) 2³ ;    б) 2⁴;            в) 4^-2;    г) 2^-3

     3.    Значення  виразу  2^-3 + 2^-2   дорівнює:

а) -10;    б) ;            в) ;              г) 12.

     4.    Тотожним до степеня ^-2  є вираз:

а) ^-2   ;        б)  в)²            г) ∙(-2)

 

VIII. Домашнє завдання

Опрацювати №265, 267, 269.

Додатково № 277, 283.

 

Урок №24

Тема уроку. Властивості степеня з цілим від'ємним показником.

Мета. Вивчити властивості степеня з цілим від'ємним показником та сформувати вміння використовувати їх для розв'язування вправ на обчислення значень числових виразів і перетворень виразів зі змінними.

Тип уроку. Засвоєння знань та первинних умінь.

Обладнання. Підручник

Хід уроку

I. Організаційний етап. Аналіз контрольної роботи

II. Перевірка домашнього завдання

Дня перевірки якості первинних знань учнів можна провести математичний диктант або, в разі необхідності, роботу з перевірки домаш­нього завдання за зразком із наступною корекцією.

Перевірка якості знань учнів у формі математичного диктанту з наступною перевіркою і корекцією помилок.

Математичний диктант

І В                                                              ІІ В

  1. Замініть степінь з цілим від’ємним показником дробом.

             а) 4^-3 ;                                               а) 5^-1;

       б) (2х)^-2 ;                                                           б) (3х)^-4.

 

2.Замініть дріб степенем з цілим від’ємним показником.

а) ;                                                        а) ;

                    б) ;                                                        б) .

  3.Обчисліть.

                а) ()^-2;                                                        а)()^-2;

б)  3^-1 +4^-1;                                                   б) 2^-1+ 5^-1.

 

IІ. Актуалізація опорних знань та вмінь

    Усно

 

1. Яке число слід піднести до квадрата, щоб дістати: 9; 81; 0; 16; ?

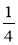Яке число слід піднести до куба, щоб дістати: 8; -27; ; -0,064?

2. Подайте вирази у вигляді степеня:

х⁵х⁷; 5 ∙ 5²; аа³; у⁴у⁶у; 10² ∙ 10 ∙10³; 7² ∙ 49³; а⁸ : а²; 3⁴ : 3; х⁶ : х; ;

а^2п ∙ а^п; (а³)²; 3² ∙ а²; а⁵ ∙ (а¹² : а²)²; -z⁶ : (-z)³.

3. Знайдіть значення виразів: 2³; 2^-3; 5²; 5^-2; 7²; 7^-2; 5³ : 5² – 5 ∙ 2^-3.

 

 Які властивості ви використовували?

  - Сформулюйте їх?

 

V. Засвоєння знань

Властивості степеня з натуральним показником справджуються і для степеня з будь-яким цілим показником (необхідно лише зауважити, що основа степеня відмінна від нуля).

Отже,

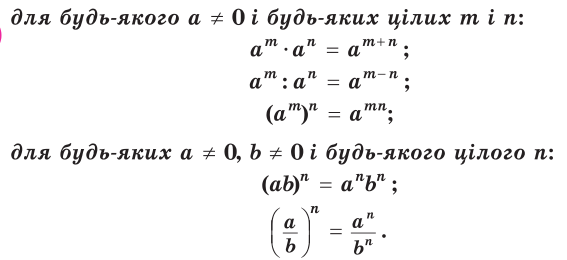
Ці властивості можна довести, спираючись на формулу                            та властивості

степеня з натуральним показником.

 Доведемо, наприклад, формулу                                   для випадку, коли m і n – від’ємні цілі числа.

 Нехай                                  , де p і q- натуральні числа. Маємо:

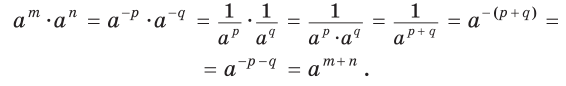
Отже,                                    якщо m і n – від’ємні цілі числа. Так само цю формулу можна довести, якщо один із показників m і n – від’ємні цілі числа, а інший – додатний або дорівнює нулю.

 

 

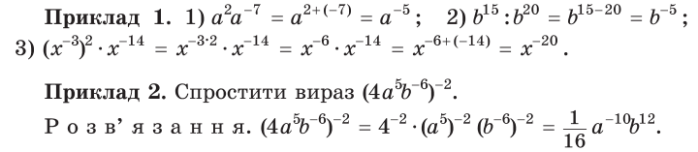
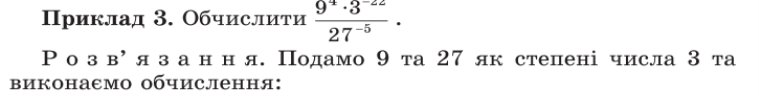
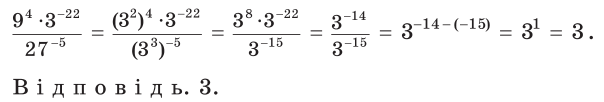
                           Опорний конспект

 

Властивості степенів з цілим показником	Прикладне застосування
	Обчисліть:
ат* а п =а т+ п	5-9* 511 =5-9+11 =52 =25
( ат)п =а т* п	(0.97-4)0 =0.97-4*0 = 0.970 =1
( аb)п =а п*
ат:а п= а т - п	4-10:4-12 = 4-10-(-12) = 42 =16

 

VI. Формування вмінь

 

Виконання усних вправ

1. Подайте у вигляді степеня вирази: b³Ь^-6; (b²)^-3; (b^-5)⁰.
2. Знайдіть значення виразів: (1,7)² 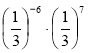(1,7)^-2; ; (-5)⁷ ∙ (-5)^-6.
3. Спростіть вирази: t^-3 : t^-5; a^-2 ∙ а³; (z^-3)^-2; (а^-1b^-4)^-2.

 

Виконання письмових вправ

Колективне розв’язування вправ на застосування властивостей степеня з цілим показником.

Пояснення вчителя            Розв’язування вправ учнями біля дошки під контролем вчителя.

№1

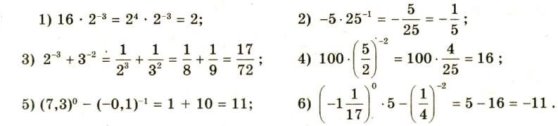
Самостійно( робота в групах)

№296

         .

 

№298

;   ;   ;  .

 

№ 300. 304.

 

Робота біля дошки.

 

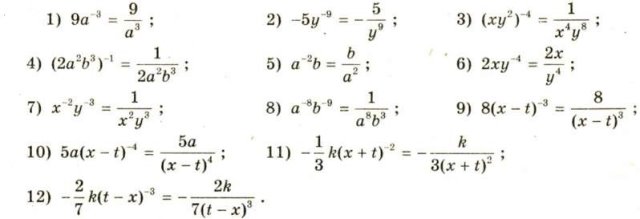
V. Закріплення знань.

1. Усна вправа „Піймай помилку”.

 

  а³_*а^-5=а²;      а^-7:а^-6=а^-13;   (а^-2)^-3=а^-5;   (а^-5)⁰=а^-5;  

2^-2_*5^-2=;   =.

2. Тести.

1)У виразі     пропущено число

а) -5;     б) 5;       в) -12;        г) 12.

   2) У виразі    пропущено число

       а) 3;       б) -3;       в) -16;        г) -8.

   3) У виразі  =m пропущено число

        а) -8;      б) 15;      в) 2;          г) 8.

     4)  Виразу     тотожно рівний вираз

       а) 2а;      б) ;        в) ;        г)  .

 

 

VII. Підсумки уроку

В якому з випадків правильно виконано дію?

1) a¹⁵ ∙ а ^-3 = а ^-5; 2) m^-12 : m^-8 = m⁸; 3) (m^-3)^-5 = m¹⁵; 4) .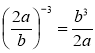

VIII. Домашнє завдання

Повторити №.297, 299, 301 -  І група,

                            № 303, 305307 – ІІ група.

 

Конспект уроку №25

Тема уроку. Властивості степеня з цілим від'ємним показником. Самостійна робота.

Мета. Закріпити знання учнів про означення та властивості степе­ня з цілим (від'ємним) показником та сформувати вміння використо­вувати їх для розв'язування вправ на обчислення значень числових ви­разів та перетворень виразів зі змінними; розвивати способи і прийоми мислення, індивідуальні здібності учнів, їх пізнавальні інтереси; виховувати охайність, уміння досягти мети, культуру математичного мовлення, інтерес до предмета.

Тип уроку. Комбінований.

Обладнання. Підручник , картки із завданнями.

Хід уроку

I. Організаційний етап

II. Перевірка домашнього завдання

Учитель перевіряє домашнє завдання. 2-3 зошити, а решта розвязують з індивідуальних карточок.

III. Формулювання мети і завдань уроку

IV. Актуалізація опорних знань та вмінь

Виконання усних вправ

1. Подайте вирази у вигляді одночлена: t² ∙ t⁵; (т³)²; а⁷ : а; (ху)⁵.
2. Спростіть вирази: t ^-3 ∙ t ⁶; а ³ : а ^-2; (а ^-6) ^-2; (а ^-5b ^-2) ^-3.
3. Обчисліть значення виразів найзручнішим способом:

2 ^-13 ∙ 2 ²⁵ : 2 ¹² ; (5 ^-5) ^-13 : (5 ^-16) ^-4; .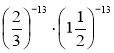

- Які властивості ви використовували?

  - Сформулюйте їх?

 

V. Відпрацювання вмінь

Виконання письмових вправ

№306, 308, 310.

№315, 317.

 

VI. Підсумки уроку

Самостійна робота

Завдання 1. а), б), в), г) та 2. а), б) – по 1,5 бали; 3 – 3 бали.

Варіант 1	Варіант 2
1. Виконайте дії:
а) 5-1 – 3 ∙ 2-3;  б) 2-10 ∙ 26; b) (x – 7)-2;         г) .	а) 6-1 – 2∙3-2;     б) 512 ∙ 5-8; в) а-3 : а-6;         г) (а-4)3 ∙ а10
2. Спростіть вираз:
a) 1x6у -10 ∙ 0,7x-4у2; б) .	а) 1а7b-12 ∙ 0,9a-5b13; б) .
3. Обчисліть:

 

Відповіді на самостійну роботу

Варіант 1

1. а) ; б) ; в) ; г) .

2. а) ; б) .

3. .

 

Варіант 2

1. а) ; б) ; в) ; г) .

2. а) ; б) .

3. 8.

 

VII. Домашнє завдання

Повторити №311, 314.

                       Конспект уроку №26

Тема уроку: Стандартний вигляд числа.

Мета: омогтися засвоєння учнями змісту понять «стандартний вигляд числа», «порядок числа»; сформувати вміння застосовувати вивчені поняття для означення запису числа у стандартному вигляді та запису даного числа у стандартному вигляді й визначення його порядку.

Тип уроку: засвоєння та формування вмінь.

Наочність та обладнання: опорний конспект «Степінь з цілим від’єм­ним показником».

Хід уроку

I. Організаційний етап

 

II. Перевірка домашнього завдання

 

III. Формулювання мети і завдань уроку

На цьому етані доречним є повторення зразків запису значень де­яких констант, з яких розпочалося знайомство учнів із поняттям степе­ня з цілим від'ємним показником. Для створення відпо­відної мотивації навчальної діяльності учнів можна запропонувати учням досить великі та малі числові значення величин, наприклад об'єм земної кулі 1 083 000 000 000 км³, діаметр молекули води 0,0000000003 м (за умови високого рівня інтелектуальної активності учнів можна організувати самостійну роботу учнів з довідниками — знайти значення різних констант із відповідної літератури), та запропонувати учням порівняти записи цих величин із записами у довіднику. Зрозуміло, що «коротший» спосіб запису більш зручний, тому завдання полягає в то­му, щоб визначити цей універсальний спосіб запису великих та малих величин, а також навчитись записувати великі й малі числа в такому вигляді. Останнє твердження виражає основну дидактичну мету теми «Стандартний вигляд числа».

 

IV. Актуалізація опорних знань та вмінь

       З метою успішного сприйняття учнями навчальною матеріалу уроку перед вивченням нового матеріалу слід активізувати такі знання і вміння учнів: виконання арифметичних дій із десятко­вими дробами, особливо множення і ділення десяткового дро­бу на розрядну одиницю; виконання дій зі степенями з цілими показниками, що передбачають застосування означення і властивості степеня з цілим показником.

 

Виконання усних вправ

1. Виконайте дії:

0,1 ∙ 0,25; 320 : 10; 10 ∙ 0,25; 320 : 100; 100 ∙ 0,25;

320 : 1000; 0,01 ∙ 0,25; 320 : 10000.

2. Подайте числа у вигляді степеня з основою 10:

10; 100; 1000; 0,1; 0,001; 0,01.

3. Які з чисел задовольняють умову 1 ≤ а < 10?

0,1; 1; 1,5; 9,99; 10; 101.

4. Знайдіть значення виразів:

(1,7)² ∙ (1,7)^-2; 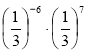; (-5)⁷ ∙ (-5)^-5.

 

V. Засвоєння знань

План вивчення нового матеріалу

1. Уявлення про запис додатного числа в стандартному вигляді; поря­док числа.
2. Як записати число в стандартному вигляді?

   Читати чи записувати дуже великі і дуже малі числа у ви­гляді десяткових дробів незручно, також незручно виконувати дії із цими числами. У таких випадках зручно використовува­ти степінь числа 10 з цілим показником і записувати число у вигляді а10ⁿ, де n — ціле число, 1 < а < 10.

Наприклад,

5 976 000 000 000 000 000 000 000 кг = 5,97610²⁴ кг;

0,00000000025 м = 2,510^-10 м.

Кажуть, що числа 5 976 000 000 000 000 000 000 000 і 0,00000000025 записано не у стандартному вигляді.

Стандартним виглядом числа називають його запис у вигляді добутку а 10ⁿ, де 1 < а < 10 і n — ціле число.

Якщо число записано у стандартному вигляді, то порядок степеня п називають порядком числа. Наприклад, порядок числа, що виражає масу Землі в кілограмах, дорівнює 24, а порядок числа, що виражає діаметр молекули водню в метрах, дорівнює -10.

У стандартному вигляді можна записати будь-яке додатне число. Порядок

числа дає уявлення про це число.

Якщо порядок числа х дорівнює 4, то це означає, що 1⁴ х< 1010⁴ тобто

10 000 < х< 100 000. Якщо порядок числа у дорівнює -2, то

1 • 10^-2 у < 10 • 10^-2, тобто 0,01 < у < 0,1.

Великий додатний порядок числа показує, що число дуже велике. Великий за модулем від'ємний порядок числа пока­зує, що число дуже мале.

Приклад 1. Подати число х = 272000у стандартному вигляді. Розв'язання. У числі х поставимо кому так, щоб у цілій частині була одна цифра, відмінна від нуля. В результаті дістанемо 2,72. Комою відокремили 5 цифр справа, тому х зменшили у 10⁵ раз. Звідси х = 2,7210⁵.

Відповідь. х = 2,7210⁵.

Приклад 2. Подати число х = 0,00013 у стандартному вигляді. Розв'язання. У числі х перенесемо кому на 4 знаки вправо, маємо 1,3. При цьому число х збільшили у 10⁴ раз. Отже, х = 1,310^-4.

Відповідь.х = 1,310^-4.

 

VI. Формування вмінь
Виконання усних вправ

1. Назвіть порядок числа, записаного в стандартному вигляді:

а) 5,49 ∙ 10⁷; б) 8,905 ∙ 10²: в) 1,2 ∙ 10¹²; г) 3,33 ∙ 10^-5.

2. При якому значенні п рівність правильна:

а) 71,3 ∙ 10ⁿ = 0,00713; б) 0,053 ∙ 10^п = 5,3?

3. Чому дорівнює ділу записах поданих чисел у стандартному ви­гляді:

а) 0,73 = а ∙ 10^п; б) 272 = а ∙ 10^п; в) 12 345 = а ∙ 10^п?

4. Чи правильно вказано значення а в стандартному записі числа:

а) 0,002 = 2 ∙ 10^п; б) 7580 = 75,8 ∙ 10^п; в) 12,5 = 1,25 ∙ 10^п?

 

Виконання письмових вправ

Для реалізації дидактичної мети на цьому уроці слід розв'язати за­вдання такого змісту:

1. Запис чисел (натуральне, десятковий додатний дріб тощо) у стан­дартному вигляді.

1) Запишіть у стандартному вигляді число:

а) 7500; б) 110 000; в) 34,17; г) 456 000 000; д) 0,035; є) 0,00015;

ж) 0,53954; з) 0,0000002.

2) Запишіть у стандартному вигляді число:

а) 52 000 000; 6) 675 000 000; в) 0,00281; г) 2180 000; д) 40,44;

є) 0,0000035.

3) Маса Землі дорівнює 6 000 000 000 000 000 000 000 т, а маса атома водню 0,000 000 000 000 000 000 0017 г. Запишіть у стандартному вигляді масу Землі і масу атома водню.

4) Запишіть у стандартному вигляді:

а) 45 ∙ 10³; б) 117 ∙ 10⁷; в) 0,74 ∙ 10⁵; г) 0,06 ∙ 10⁵.

2. Запис у вигляді десяткового дробу чисел, що записані у стандарт­ному вигляді.

Запишіть у вигляді десяткового дробу число:

а) 1,2 ∙ 10³; б) 3,5 ∙ 10⁵; в) 4,2 ∙ 10^-3; г) 5,7 ∙ 10^-5.

3. Запис у стандартному вигляді значення величини з попереднім переходом до інших одиниць вимірювання.

1) Подайте:

а) 1,9 ∙ 10¹⁵ г у тоннах;   б) 2,8 ∙ 10^-1 т у кілограмах;

в) 5,2 ∙10^-3 м у сантиметрах;  г) 6,12 ∙ 10² м у дециметрах.

2) Виразіть:

а) 3,8 ∙ 10³ т  грамах;   б) 1,7 ∙ 10^-4 км у сантиметрах;

в) 8,62 ∙ 10^-1 кг у тоннах;   г) 5,24 ∙ 10⁵ см у метрах.

4. Логічні вправи та завдання підвищеного рівня складності для учнів, які мають достатній та високий рівні знань.

1) Виразіть час у секундах і запишіть здобуте число у стандартному
вигляді:

а) 1 година; б) 1 доба; в) 1 рік; г) 1 століття.

2) Вставте пропущене число:

 

59000000 = 5,9 0,00000000265 = 2,65 1860000000000000 = 1,86

 

      (Виконуючи вправи на закріплення поняття стандартного ви­гляду числа, учні набувають навичок визначення порядку чис­ла, переходу від звичайного запису до запису числа в стандарт­ному вигляді, і навпаки.)

Робота з підручником

№ 335, 337,339, 340.

 

VII. Підсумки уроку

В якому з випадків правильно записане число у стандартному ви­гляді?

1) 0,1002 = 1,2 ∙ 10³; 2) 0,1002 = 1,002 ∙ 10³; 3) 0,1002 = 1,002 ∙ 10^-1;

4) 0,1002 = 1,002 ∙ 10^-4.

 

VIII. Домашнє завдання

1. Вивчити зміст поняття «стандартний  вигляд числа», «порядок числа».
2. Розв'язати вправи на застосування вивченого поняття (змісту, ана­логічного до вправ класної роботи).
3. На повторення: означення і властивості степеня з цілим показни­ком, виконати вправи на їх застосування.
4. вивчити , № 336, 338, 341.

 

                     Конспект     уроку №27

Тема : Розв’язування вправ. Самостійна робота.

Мета  уроку:

• навчальна – Формування вмінь і навичок учнів в практичному                      застосуванні вивчених правил для виконання дій із числами, записаними  у стандартному вигляді, при розв’язанні задач на уроках фізики, хімії та астрономії;
• розвивальна – розвивати інтерес учнів до  математики.
• виховна – виховувати в учнів цікавість; створення  позитивного емоційного фону на уроці.

Тип уроку: урок формування вмінь і навичок

Хід  уроку

І. Організаційний момент.

ІІ. Перевірка домашнього завдання:

Індивідуальні картки.

Картка 1

1. Записати число у стандартному вигляді.

56,8;   34800000000;   259000000000000;

0,0000024;    0,00178;      0, 00000000000465.

2. Записати натуральним числом чи десятковим дробом.

5,24;   8,521;   9,3;

7,217,154;   1,06.

Картка 2

1. Записати число у стандартному вигляді.

6,81;   83400000000;   200590000000000;

0,00000644;    0,00568;      0, 0000097.

2. Записати натуральним числом чи десятковим дробом.

6,4;   8,1;   9,73;

7,51,65;   5,6.

Картка 3

1. Записати число у стандартному вигляді.

21,8;   37000000;   25000000000;

0,00048;    0,001056;      0, 0000000000065.

2. Записати натуральним числом чи десятковим дробом.

6,4;   8,1;   9,653;

6,15,14;   4,06.

Картка 4

1. Записати число у стандартному вигляді.

50,8;   80340000000;   741000000000000;

0,094;    0,007578;      0, 0000000005.

2. Записати натуральним числом чи десятковим дробом.

2, 54;   2,851;   9,3;

7,217,154;   2,76.

 

IІІ. Актуалізація опорних знань та вмінь:

Який вигляд має число записане в стандартному вигляді?

Що таке порядок числа?

Що означає збільшити число на порядок?

 

Виконання тестових завдань.

 

IІІ. Розв’язання вправ: ( Робота в групах. Кожна група презентує розв’язання своєї задачі перед класом)

 

Фізика. 8 клас.		Тема: Звук.
Три пластини, що розташовані в просторі, коливаються. Частота коливань першої пластини  50 Гц, другої – 500 Гц, третьої – 5 кГц. Які з пластинок  є джерелами звуку?
Дано : ν1= 50Гц ν2= 500Гц ν3= 5кГц = =5 ·103Гц=500Гц	Розв’язок: Всі три пластини є джерелами звуку, так як вони коливаються з частотою, що лежить в діапазоні звукової частоти від 16 Гц до 20 000 Гц. (частоти, яку сприймає людина)
ν - ?

================================================================================

 

 

 

Фізика. 8 клас.			Тема: Робота і потужність.
Визначити потужність машини, що піднімає молот вагою 1,5кН на висоту 80см за 2 с.
Дано : Р=1,5кН=1,5·103; H=80 см =8·10-1м t=2c	N=A:t A=F·s	Розв’язок: A= F · s =P · h; А = 1,5 · 103Н·8·10-1м=12·102Дж=1,2·103Дж; N=1,2·103Дж : 2с=6·102Вт= 6 гВт.
N - ?

================================================================================

Хімія. 8 клас.		Тема: Кількість речовини.
№1. Вкажіть число молекул , що містяться у кисні кількістю речовини 1,5 моль.
Дано : ν(О2)=1,5моль	Розв’язок:  N(О2)=NA ·ν=6,02 · 1023моль-1·1,5моль=9,03·1023
N(О2)-?

================================================================================

Хімія. 8 клас.		Тема: Кількість речовини.
№2. Розрахуйте масу 3,01·1023  атомів Алюмінію.
Дано : N(Al)=3,01·1023	Розв’язок:  m(Al)=N·ν; ν= N:NA=3,01·1023:6,02·1023моль-1=0,5моль m(Al)=0,5моль·27г/моль=13.5г
m(Al)=?

================================================================================

Астрономія.
Маса Землі дорівнює 5,98•1024 кг, а маса Марса – 6,4•1023 кг. Що більше: маса Землі чи маса Марса  й у скільки разів? Результат округліть до десятих.
	Розв’язок:  Маса Землі більша за масу Марса, оскільки порядок маси Землі більший (24›23). Маса Землі більша у 0,93·10≈0,9·10 разів.

================================================================================

Додаткові номера: №354, 355, 358.

ІV. Підсумок уроку.

Ми з вами побачили взаємозв’язки між окремими шкільними предметами і навчилися застосовувати  знання з алгебри при розв’язанні задач з фізики, хімії та астрономії.

 

V. Домашнє завдання.

§ 11, №345, 347, 349.

Повторення. Функції.

 

Урок 28

Тема: "Функція  y, її властивості і графік".

 

 

Мета:	Освітня: Ввести поняття оберненої пропорційності. Розглянути властивості функції y, застосовувати вивчений матеріал для побудови графіків; формувати вміння визначати і описувати властивості функції по графіку.  Сформулювати визначення оберненої пропорційності, навчити знаходити значення функції і аргументу за формулою y,  сприяти виробленню навичок і вмінь у побудові графіка функції виду y .  Розвиваюча: Сприяти формуванню інформаційної компетентності: вміння систематизувати, аналізувати, порівнювати, робити висновки. Прилучати учнів до самостійної діяльності; сприяти розвитку навичок самоконтролю і взаємоконтролю в процесі виконання завдань. Виховна: виховувати в учнів акуратність, культуру поведінки, почуття відповідальності; прищеплювати графічну культуру; виховувати вміння аналізувати свою роботу і роботу однокласників. Корекційна: продовжувати працювати над грамотною усною і письмовою промовою учнів, корегувати дрібну моторику, поставу.
Обладнання:	Комп’ютер, презентація, роздаткові матеріали.

 

Хід уроку

1. Організаційний момент.
2. Перевірка домашнього завдання.

Тестова робота

1. Який із записів є стандартним виглядом числа 0,3005?

 

А	Б	В	Г
3,5 ∙ 10-3	3,005 ∙ 103	3,005 ∙ 10-1	3,005 ∙ 10-3

 

2. Укажіть порядок числа 0,353.

 

А	Б	В	Г
3	2	-3	-1

 

3. В якому випадку дію (3 ∙ 10^-5) ∙ (1,2 ∙ 10²) виконано правильно?

 

А	Б	В	Г
3,6 ∙ 10-3	3,6 ∙ 107	0,36 ∙ 102	0,36 ∙ 10-3

 

4. В якому випадку ділення виконано правильно?

 

А	Б	В	Г
(2∙105):(4∙102) = = 0,5 ∙ 103	(2∙105):(4∙102) = = 5 ∙ 102	(2∙105):(4∙102) = = 500	(2∙105):(4∙102) = = 8∙107

 

5. Актуалізація опорних знань учнів.

Слайд 2. Давайте повторимо, що ми знаємо про функцію із 7-го класу.

1. Функцією називають залежність….
2. Область визначення функції…
3. Область значення функції…
4. Графіком функції називають точки…
5. Функцією виду , називають….
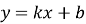
6. Графіком лінійної функції є…     (разом)
7. Як пов'язані між собою швидкість і час?
8. Якщо при збільшенні незалежної змінної (x)

збільшується залежна  (y), то це…

 

Ігровий момент

 

Уявіть собі, що на Землі відбулась плутанина і для процесів, що описуються прямою пропорційністю, використовують обернену пропорційність і навпаки.

 

Тоді б ми говорили:

 

- Чим більше купуємо цукерок, тим .... (менше сплачуємо грошей).

 

- Чим довше горить свічка, тим... (вона довша і т. ін.)

 

Придумайте свої подібні переплутані висновки.

 

6. Вивчення нового матеріалу.

Презентація на компютері.

Слайд 3. Завершіть речення:
 

а) Зі збільшенням ціни кількість товару, яку можна закупити на  дану суму грошей ...

                                                                               зменшиться

 

б) Зі зменшенням швидкості руху на на однаковій відстані час руху ... 

                                                                               збільшиться

 

в) Зі збільшенням продуктивності праці при виконанні даного обсягу роботи кількість часу, потрібного для виконнання роботи ...  

                                                                              зменшиться

 

У цих прикладах дві величини такі, що збільшення однієї в декілька разів тягне за собою зменшення іншої величини у ту саму кількість разів і навпаки — такі величини будемо називати обернено пропорційними.

 (Можна запропонувати учням спробувати навести інші приклади обернено пропорційних величин з повсякденного життя.)

 

Слайд 4.

Приклад:

• Відстань 120 км. велосипедист  долає зі швидкістю 12 км/год., вантажівка км/год, автомобіль км/год. Який час потрібен кожному для подолання цієї відстані?

Розв’язання:

;  

10 (год.); 

 3 (год.);

 2 (год.)

• Збільшення швидкості веде до зменшення часу, і навпаки, якщо швидкість зменшується, то час збільшується.
• У розглянутому прикладі реальної ситуації є функція, яку можна задати формулою виду:  .

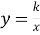Слайд 5. Означення.

Слайд 6. Історична довідка

Слайд 7. Властивості  функції

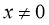1. Область визначення функції:  множина всіх чисел, відмінних від нуля.
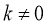
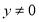2. Область значень функції: множина всіх чисел, відмінних від нуля.

 

Слайд 8. Розв’язування вправи на знаходження оберненої пропорційністі.

 

 

Слайд 9. Побудова графіка функції .

Графік не має спільних точок із віссю абсцис і ординат. Число 0 не належить області визначення і області значень функції.

Фігуру, яка є графіком функції  , називають гіперболою. Гіпербола складається з двох частин – гілок гіперболи.

Область визначення	Усі числа
Область значень	Усі числа, крім 0
Графік	Гіпербола
Нуль функції	Не існує

 

 

 

 

    1 ) Складемо таблицю значень для х і у;

2 ) Накреслимо координатну площину;

3) Проставимо точки в координатній площині;

4) З’єднаємо точки плавною лінією.

 

Слайд 10.

Побудуємо графік функції .

 

Отже, якщо , то графік розміщений у I і III чвертях,

 

Слайд 11.

Побудуємо графік функції .

Отже, якщо , то графік розміщений у II і IV чвертях.

 

                V. Фізкультхвилинка

 

VI. Закріплення вивченого.

 

Слайд 12-14

№2  Побудуємо по точках графік функції    в тій же системі координат, що й графік функції

 

Слайд 15

Порівняємо ці графіки. Як вони розташовані? Яку залежність відстані до осей координат від модуля ви помітили?

 

Слайд 16

Отже…

1. Якщо k>0, то гілки гіперболи розташовані в ... і ... координатних чвертях.
2. Якщо k <0, то гілки гіперболи розташовані в ... і ... координатних чвертях.
3. Чим більше по модулю k, тим   далі розташовані гілки гіперболи від осей координат.

 

Слайд 17   №3  Знайдіть відповідність. (4б)

Слайд 18   №4      Знайдіть за графіком функції значення у, відповідне значенню х,

рівному 2;  4;  -1;  -4;  -5.

 

Слайд 19   №5    Знайдіть за графіком значення х, якому відповідає значення у,                рівне    -4;  -2;   8

Слайд 20   №6     Задайте функцію  оберненої пропорційності, якщо її графік проходить через точку А( 5; 3 )

 

Самостійно :             В(-6; -2)

Слайд 21   №7    Знайти на якому рисунку зображено графік функції              

 

Додатково

№ 8     Чи належать графіку функції точки A (-4; -7) ;  В (14; -2)

           А  є графіку функції        ;

           В  не є графіку функції       .

7. Підсумки вивченого:

1. Поставте у відповідність рисунки і рівняння функцій:

 

а)	б)	в)	г)
1) у= |х|;	2) y = 3;	3) y = kx + b;	4) у = х2.

2. На якому з наведених рисунків зображено ескіз графіка функції ?

 

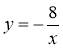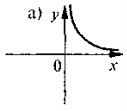
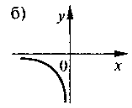
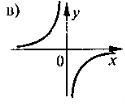
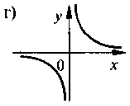
3. висновки;
4. виставлення оцінок.

 

8. Завдання додому.

Вивчити означення та властивості оберненої пропорційності.

Розв'язати вправи на застосування вивчених властивостей.

На повторення: означення та властивості лінійної функції; виконати
вправи на побудову графіка лінійної функції та аналітичного способу
знаходження координат точок перетину графіків лінійних функцій.

§12, № 370, 372, 376.

 

1Слайд 22         Рефлексія

 

 

Конспект уроку №30

Тема: Розв’язування вправ

Тип уроку: закріплення вивченого матеріалу.

Мета:

Освітня: повторити властивості функції виду ;закріпити навички побудови графіка функції виду ;формувати вміння визначати й описувати властивості функції за графіком.

Розвиваюча: прилучати учнів до самостійної діяльності; сприяти розвитку навичок самоконтролю й взаємоконтролю в процесі виконання завдань.

Виховна: виховувати  в учнів акуратність, культуру поведінки, почуття відповідальності; прищеплювати графічну культуру; виховувати вміння аналізувати свою роботу й роботу однокласників.

Обладнання:  комп'ютер, презентація, дошка, крейда, підручник, збірник завдань, оцінний аркуш, аркуші навчальної успішності, аркуші із завданнями для самостійної роботи, аркуші з питаннями до кросворда, картки з додатковим завданням, картка на повторення.

Хід уроку:

1.   Організаційний. (1 хв)

Перевірка готовності учнів до уроку, настрой на початок уроку, вітання.

2.   Постановка мети. (1 хв)

Повідомлення теми, мети, мотивація навчальної діяльності. На дошці: число, тема.

Ми з вами на минулому уроці ознайомилися з  функцією y = . , її графіком і властивостями. Як ви гадаєте, чому ми маємо присвятити цей урок?

— Навчитися користуватися  вивченими властивостями функції y =   при розв’язуванні прикладів і задач..

Учитель. Діти сьогодні на уроці ми повторимо з вами властивості функції виду ,закріпимо навички побудови графіка функції виду і будемо продовжувати вчитися грамотно описувати властивості цієї функції за графіком.

Тож до роботи.

Девіз уроку:  «Математику не можна вивчити спостерігаючи як це робить сусід» А.  Нівен

3.   Перевірка Д/з. (5 хв)

   Удома кожен із вас вивчив означення та властивості оберненої пропорційності. Як ви впоралися з цією частиною домашнього завдання, ми перевіримо наступним чином. Учні  повинні розв'язати  кросворд.

 

Г

р

а

ф

і

к

ф

у

н

к

ц

І

я

о

П

и

с

а

р

г

у

м

Е

н

т

о

Р

д

и

н

а

т

а

а

Б

с

ц

и

с

а

к

О

е

ф

і

ц

і

є

н

т

т

а

б

Л

и

ц

я

ф

о

р

м

у

л

А

Питання

1. Множина усіх точок координатної площини, абсциси яких дорівнюють значенню аргументу, а ординати відповідають значенням функції.?
2. Залежна змінна?
3. Один зі способів задання функції?
4. Незалежна змінна?
5. Як називається вісь у?
6. Як називається вісь х?
7. Як називається значення k у формулі ?
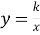8. Один зі способів задання функції?
9. Один зі способів задання функції?

4.   Актуалізація знань. (4 хв)

Підготовка до діяльності через повторення й актуалізацію опорних знань.

Після заповнення кросворда зачитується термін, який вийшов по вертикалі (гіпербола), запитую в учнів, що він означає і даю короткий історичний опис.

Розповідь:

Отримана крива називається гіперболою, що в перекладі із грецької мови дослівно означає «проходжу через що- або» і із часом одержало друге значеннєве значення «перебільшення».
 Одним з перших, хто почав вивчати цю криву був учень знаменитого Платона, давньогрецький математик Менехм в IV в. до н.е., але так і не зумів її повністю вивчити.

А от повністю досліджував властивості гіперболи й дав їй назву найкращій геометр стародавності Аполоний Пергский в III в. до н.е.

Він показав, що гіпербола виходить, якщо взяти довільний круговий конус, порожнини якого простираються по обидві сторони від вершини, і перетнути обидві його порожнини площиною, паралельної прямій  АА₁.

 

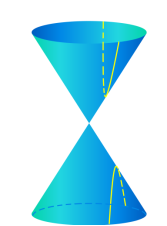Тепер почасти зрозуміло, чому крива одержала таку назву: ми побачимо її в перетині щораз, коли площина проходить через обидві порожнини конуса

5.   Усна робота. (8 хв)

Проводиться за допомогою презентації. Опрацьовуються навички побудови графіка функції виду ;формується вміння визначати й описувати властивості функції за графіком.

Опитування.

Давайте розглянемо наступне завдання.

Даний прямокутник зі сторонами x, y і площею рівної 24 дм². Використовуючи знання з курсу геометрії запищіть вираз для знаходження площі прямокутника? (x* y=8)
 Але що буде відбуватися зі стороною y, якщо сторону x зменшити в 4 рази, за умови, що площа отриманого прямокутника не зміниться? (збільшиться в 4 рази)
А як це довести алгебраїчно? ()
А що відбудеться зі стороною y, якщо сторону x збільшити в 2 рази? (зменшиться в 2 рази)
Висновок: при збільшенні однієї змінної в кілька раз друга змінна зменшується в стільки ж раз.
І навпаки, при зменшенні однієї змінної в кілька раз друга змінна збільшується в стільки ж раз.
 Як ви думає можна назвати таку залежність змінних? ( обернена пропорційність). У загальному виді така залежність записується формулою .

Підіб’ємо підсумки вашої роботи, узагальнимо все, що ми повторили і зробимо опорний конспект.. Одного із учнів я запрошую до дошки.

       Функція y = -

1. Область визначення –
2. Область значень –
3. Графік –
4. Якщо k > 0
5. Якщо k < 0

6.   Фізкультхвилинка для очей. (1 хв)

-Сядьте прямо, опустіть руки вниз, закрийте очі.

Ви перебуваєте на березі моря. Яке блакитне небо! Як яскраво світить сонце, з моря дме легкий вітерець, ви спокійні й думаєте тільки про море.

(Пауза)

-Нахиліть голову вперед, робимо кругові рухи головою вправо, уліво

-Відкрийте очі, встаньте, тихенько сядьте.

-Продовжимо.

7.   Закріплення теми. (10 хв)

Давайте побудуємо графік функції . Що для цього нам необхідно? (заповнити таблицю)
 Один учень (інші в зошитах) будує таблицю значень функції на дошці.
 Що є наступним етапом побудови графіка функції? (Побудова на координатній площині.)
 Побудова точок на дошці і на роздавальних аркушах із системами координат.  По побудованих точках дуже важко судити про весь графік функції. Адже точки можна з'єднати як завгодно. Як ви пропонуєте з'єднати побудовані точки?
Після дослідження властивостей функції   учні роблять висновки: 
1. Графік не перетинає ні вісь абсцис, ні вісь ординат;
2. Графік розташований в I і III координатних чвертях (y= 24/x)

3. Графік розташований в IІ і IV координатних чвертях (y= -24/x)
Виходить, з'єднати точки можна тільки одним способом, послідовно з’єднуючи точки зліва на право.Учні з'єднують точки на дошці й у зошитах.

8.   Перевірка засвоєння знань у вигляді самостійної роботи. (8 хв)

У завданнях 1-4 виберіть одну правильну відповідь і позначте її в бланку відповідей

1. В яких координатних чвертях розташований графік функції у = ?

А) I, IV;   Б) I, II;   В) II, IV;   Г) I, III.

2. Знайдіть значення функції y = - .  , якщо x = 2,5.

А) -4;   Б) 0,4;   В) -0,4;   Г) 4.

3. Які з наведених функцій є оберненою пропорційністю?

А) у = ;   Б) у = + х;   В) у = ;   Г) у = - .

4. Знайдіть значення аргументу, при якому значення функції   дорівнює  - 3.

А) – 4;   Б) 4;   В) 2;   Г) – 2.

Завдання 5  передбачають установлення відповідності. До кожного твердження, позначеного цифрою, виберіть твердження, позначене буквою і зробіть і поставте позначки на перетині відповідних рядків (цифри) і стовпчиків (букви).

5. Установіть відповідність між графіками функцій (1 – 4) і точками, які їм належать (А – Д).

 

1) у = -	А) (- 12;2)
2) у =	Б) (-2; 5)
3) у = -	В) (10; - 1,5)
4) у =	Г) (8;1)
	Д) (4;4)

 

 

9.   Взаємоперевірка самостійної роботи. (2 хв)

Учні обмінюються роботами. На екран виводиться виконана робота. Діти  оцінюючи роботи один одного, здають учителеві.

10. Підсумки уроку. (3 хв)

• Сформулюйте алгоритм побудови графіка функції виду .
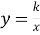• Сформулюйте залежність розташування гілок гіперболи в координатній площині від коефіцієнта пропорційності k.
• Виставляються оцінки за роботу на уроці.

11. Постановка Д/з. (1 хв)

Домашнє завдання із слайда, записали в щоденники, відкрили, подивилися, чи є питання?

12. Рефлексія. (1 хв)

Отже, ми виконали з вами всі заплановані на сьогоднішній урок завдання. А зараз я прошу вас скласти сенкан до слова «урок»

Сенкан — це вірш, що складається з п’яти рядків.

 Слово ”сенкан” походить від французького слова ”п’ять” і позначає вірш у п’ять рядків.

 1. Перший рядок має містити слово, яке позначає тему (звичайно, це іменник)

 2. Другий рядок – це опис теми, який складається з двох слів (два прикметника)

 3. Третій рядок називає дію, пов’язану з темою, і складається з трьох слів (звичайно це дієслова).

 4. Четвертий рядок є фразою, яка складається з чотирьох слів і висловлює ставлення до теми, почуття з приводу обговорюваного.

 5. Останній рядок складається з одного слова — синоніма до першого слова, в ньому висловлюється сутність теми, ніби робиться підсумок.

.

 Учні складають сенкан. Наприклад:

Урок

Цікавий, хвилюючий

Удосконалювали, досліджували та вчилися

Наступний етап підготовки до життя

Заняття.

Отже, робимо висновок, що: замало вивчити правила чи формули, треба навчитися ними користуватися, тобто застосовувати повсякденному житті

 

 

 

 Домашня самостійна робота

Варіант 1

1. Функцію задано формулою

а) Знайдіть значення функції при значенні аргументу: -2; 4.

б) При якому значенні аргументу функція дорівнює -4; -16?

в) Які з точок А(-0,5; 32); В(32; 0,5); С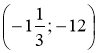; D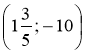належать графіку функції?

г) Побудуйте графік функції.

д) За допомогою побудованого графіка розв'яжіть рівняння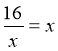

 

Урок № 31

 Тема: Контрольна робота

Мета: Перевірити засвоєння учнями даної теми.

                                                                Контрольна робота №3                                                       8 кл.

                                                                                Варіант 1

І рівень

         У завданнях 1-3 виберіть правильну відповідь.

1. Значення виразу 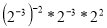дорівнює: а) 10;     б) 32;      в) 7.
2. Стандартним виглядом числа 0,027 є: а) 27*10^-3;   б) 2,7*10^-2;     в) 0,27*10^-1.
3. Графік функції 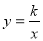для 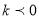зображений на рисунку:

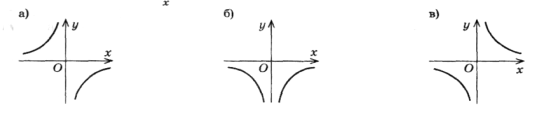
ІІ рівень

4. Знайдіть значення виразу .
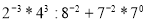5. Запишіть числа 0,0081 та 40,002 у стандартному вигляді та знайдіть їх добуток. Відповідь запишіть у стандартному вигляді.
6. На рисунку зображено графік функції 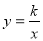. За координатами точки А знайдіть 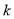та запишіть цю функцію. Користуючись одержаною формулою знайдіть:

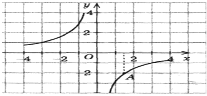а) х, якщо у = -60;       б) у, якщо х = 0,001.

 

 

ІІІ рівень

7. Знайдіть значення виразу: а) 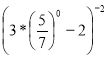;    б) .
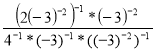8. Спростіть вираз 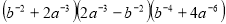та знайдіть його значення, якщо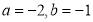

IV рівень

9.Побудуйте графік функції . Чи проходить цей графік через точку М(-0,1; -10); В(100

                                                                                Варіант 2

І рівень

         У завданнях 1-3 виберіть правильну відповідь.

1. Значення виразу 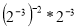дорівнює: а) 1;     б) 8;      в) 4.
2. Стандартним виглядом числа 0,271 є: а) 27,1*10^-2;   б) 2,71*10^-1;     в) 271*10^-3.
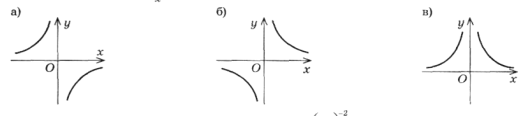
3. Графік функції 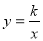для 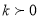зображений на рисунку:

ІІ рівень

4. Знайдіть значення виразу .
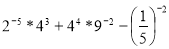5. Запишіть числа 800,8 та 0,00125 у стандартному вигляді та знайдіть їх добуток. Відповідь запишіть у стандартному вигляді.
6. На рисунку зображено графік функції 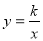. За координатами точки А знайдіть 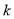та запишіть цю функцію. Користуючись одержаною формулою знайдіть:

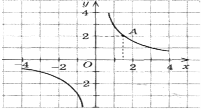а) х, якщо у = 30;       б) у, якщо х = -15.

 

 

ІІІ рівень

7. Знайдіть значення виразу: а) 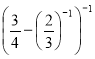;    б) .
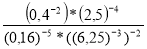8. Спростіть вираз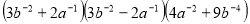та знайдіть його значення, якщо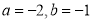

IV рівень

9. Побудуйте графік функції 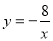. Чи проходить цей графік через точку А(-0,8; 10); В(0,001; -8000).

 

Урок 32

Тема: Аналіз контрольної роботи. Розв’язування задач.

Мета: здійснити корекцію прогалин у знаннях учнів.; сформувати сталi вмiння застосувати набутi знання в розв’язуваннi завдань базового, середнього та достатнього рiвнiв, змiст яких вiдповiдає програмовим вимогам.

Тип уроку: корекції  знань, умiнь та навичок.

Хід уроку

1. Аналіз контрольної роботи.
2.  Розв’язування вправ.

 Виконайте усно:

1) подайте вираз у вигляді степеня:

;

2) спростіть вираз:

а) ;

б) ;

в) ;

г) ;

3) розмістіть у порядку спадання:

(0,2)^-6; (0,2)⁰; 0,2; (0,2)^-4; (0,2)³.

     Відповіді: (0,2)^-6; (0,2)^-4; (0,2)⁰; 0,2; (0,2)³.

4) обчисліть:

.

     Відповіді: 625; 4; 0,04; 1/49.

5) при яких значеннях х правильна рівність:

.

     Відповіді: х=4; х=-3; х=-4; х=3; х=-2; х=2.

     Учитель. У 5—7-х класах ми розглянули степінь з натуральним показником, цілим невід'ємним показником. У 8-му класі ми вже розглядаємо степінь з цілим від'ємним показником.

3.      Дайте означення степеня з цілим від'ємним показником. (Учні відповідають.)

     Ми розглянули, що дії зі степенями з цілими показниками виконуються за тими ж правилами, що і дії над степенями з натуральними показниками.

     Повторимо їх.

— Які дії ми вміємо виконувати зі степенями?

— Як перемножити степені з однаковими основами?

— Як розділити степені з однаковими основами?

— Як піднести степінь до степеня?

— Як піднести добуток виразів до степеня?

— Як піднести дріб до степеня?

     III. Розв'язування вправ (робота в парах)

 Для учнів пропонуються  завдання записати числа у стандартному вигляді і навпаки.

. Сонячна система

Сонячна система складається з центрального тіла Сонця і 8 планет Меркурій Меркурій Венера Венера Земля Земля Марс Марс Юпітер Юпітер Сатурн Сатурн Уран Уран Нептун Нептун

 

 Сонце – центральна зірка, що домінує в Сонячній системі Екваторіальний діаметр Сонця становить – 1392000км, Температура ядра – 14 000 000 °C

Земля – планета, на якій ми живемо Середня відстань від Землі до Сонця Середня відстань від Землі до Сонця км Температура ядра Землі 6200°C, Маса Землі 5976 00000000000000000000кг Обєм Землі 1084 000000000 км3

Атоми Атоми найдрібніші структурні одиниці, з яких складаються фізичні тіла. Утворюючи між собою зв'язки, атоми об'єднуються в молекули і великі за розміром тверді тіла. Розмір атому водню  м

 

IV. Виконання тесту

     Учням пропонується тест, при його виконанні вони повинні знайти букви, з яких утворюється прізвище німецького вченого-математика «Штифель», який вніс значний вклад у розвиток поняття «Степінь». (Учні, які швидше виконали завдання, допомагають іншим).

1. Обчислити: 3^-3.

 

П 9; Ш 27 ; А -27; В -9.

2. Обчислити: .

Р ; И ; О ; T .

3. Обчислити: (-0,7)^-1.

Ф -7; Л ; И ; X .

4. Подайте у вигляді дробу: .

О a⁸; И a¹³; Ф a; A a¹².

5. Виконайте дії: .

М ; E ; Г 2x^-7y^-7; У -2x³y⁷.

6. Знайти значення виразу: .

О ; Е 245; Н ; Л .

7. Яке число найбільше: 0,5²; 0,5³; (-0,5)^-5; (-0,5)^-6.

Д 0,5²; Р 0,5³; С (-0,5)^-5; Ь (-0,5)^-6.

 

VІ. Робота в групах

1. Функцію задано формулою . Заповніть таблицю:

 

х	- 4		- 0,25	2	5	16
у		- 4					0,4

 

2.Перевірити, чи належать графіку функції точки із заданими коор­динатами (знайти невідому координату графіка функції за відомою іншою або задати обернену пропорційність, якщо відомі координати точки графіка цієї функції).

1) Чи належать графіку функції точки: А(-8; 1), В(-4; -2), С(-2;4), D(-0,5; 8)?

2) Відомо, що деяка функція — обернена пропорційність. Запишіть цю функцію формулою, знаючи, що значенню аргументу, що дорівнює 2, відповідає значення функції, що дорівнює 12.

3) Рухаючись зі швидкістю v км/год, потяг проходить відстань між містами А і B, яка дорівнює 600 км, за t год. Запишіть формулу, яка виражає залежність: a) v від t; б) t від v.

4) Побудуйте графік функції:

a) ; б) .

V. Домашнє завдання

1) Побудуйте графік функції . Користуючись графіком, знай­діть значення функції, які відповідають таким значенням аргумен­ту: -2,5; 5.

2) Побудуйте графік функції, заданої формулою . Знайдіть за графіком:

а) значення у, яке відповідає значенню х, що дорівнює: 4; 2,5; 1,5; -1; -2,5;

б) значення х, якому відповідає у, яке дорівнює: 8; -2.

3) Задайте формулою обернену пропорційність, знаючи, що її гра­фік проходить через точку:

а) A(8; 0,125); б) В 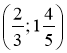; в) С(-25; -0,2).

 

 

VІ. Підбиття підсумків уроку

    Учитель формулює незавершене речення, а учням пропонується продовжити його за підсумками своєї діяльності під час уроку:

• Сьогодні на уроці я дізнався...

• Найбільше труднощів було...

• Найбільше мені сподобалося...

• Надалі я буду більш успішним, тому що...

     Відповіді учнів дозволяють учителю мати уяву про характер труднощів, які мають учні під час вивчення цієї теми, а також будуть формувати в учнів бажання бути більш успішними і надалі.