конспектРозробка уроку з геометрii у 7 класi " властивостi та ознака рiвнобедреного трикутника" уроку

Урок геометрії    7 клас.

Рівнобедрений трикутник та його властивості

 

Тема. Рівнобедрений  трикутник  та  його   властивості.

Мета. Ввести  поняття  рівнобедреного  та рівностороннього  трикутників  і  їх  елементів, вивчити  ознаку  і  властивості  рівнобедреного  трикутника. Розвивати  вміння  виділяти  головне, порівнювати  та  узагальнювати, логічно  викладати  свою  думку, виховувати  в  учнів  інтерес  до  предмету.        

Тип   уроку: комбінований урок

Обладнання: презентація «Рівнобедрений трикутник і його властивості»

Хід  уроку:

І. Організаційний момент.

Вітаюсь. Перевіряю готовність учнів до уроку.

 

ІІ. Актуалізація опорних знань учнів

1. Вправа «Асоціативний кущ»

З якими словами у вас асоціюється слово «трикутник»?

Слайд 3

 

Робота з презентацією

Усні вправи.

 

 

 

 

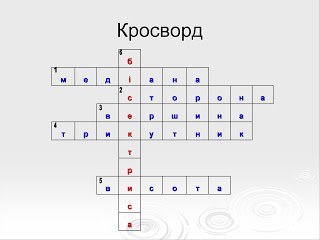
2. Кросворд

 Слайд 4   (слова з’являються після  відповідей учнів)

 

 

1.     Як називається відрізок, що сполучає вершину із серединою  протилежної сторони трикутника? (медіана)

2.  Фігура, яка складається з  трьох  точок, що  не лежать  на  одній  прямій, і  трьох  відрізків, які  попарно  сполучають  ці  точки… Як називається один  з  таких відрізків? (сторона)

3.     Як  називається  одна  з  таких  точок? (вершина)

4.     Як  називається  ця  фігура? (трикутник)

5.     Як  називається   перпендикуляр, проведений  з  вершини  до  прямої, що  містить  протилежну  сторону  трикутника? (висота)

6.  Як  називається  відрізок, що  сполучає  вершину  з  точкою  на протилежній  стороні  і  ділить  кут  при  вершині  пополам? (бісектриса)

       Після  роботи  над  кросвордом, пропоную  трьом учням  на  дошці  схематично  зобразити  гострокутний, тупокутний  та  прямокутний  трикутники.

ІІІ. Формування нового навчального матеріалу.

Робота з презентацію   «Трикутники»

 

 

 

 

 

Робота з рисунком

Виміряти сторони трикутника та встановити його вид.

Рисунки

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

2. Оголошення  теми  і  мети  уроку.

Слайди 1

 

 

 

 

 

 

3. Вивчення нової теми.

Слайд 5.

 

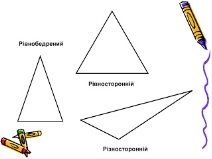
        Трикутник, у  якого  дві  сторони  рівні  називається   рівнобедреним. Рівні  сторони  називаються  бічними  сторонами, а  третя  сторона – має  назву   основа. Якщо  ж  у  трикутнику  всі  сторони  рівні, то  такий  трикутник  називається  рівностороннім. (На  екрані поступово з’являються зображення різностороннього, рівностороннього  та  рівнобедреного  трикутників)

        Де  потрібні  знання  про  рівнобедрений  трикутник? Насамперед  у  математиці – при  розв’язуванні  задач  та  при  доведенні  різних  тверджень, у  кресленні, на  будівництві, у  конструкторських  бюро, на  заводах, в  кораблебудуванні, пілотам, морякам, фермерам  і  т.д.

        Які  ж  властивості   має  рівнобедрений  трикутник?

 

Учні отримують таблицю

Слайд 6

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Теорема. (властивість кутів)

1.У рівнобедреного трикутника кути при основі рівні.

 

2 . У  рівнобедреному  трикутнику  бісектриса, проведена  до  основи  є  медіаною  і  висотою.

 

 

Якщо   ж  це  теорема, то   її  потрібно   довести.

 Що  дано? (відповіді  учнів).

 Що  потрібно  довести? (відповіді  учнів).

                                В                                                                        Дано:                       

                                      
                                                                                                трикутник АВС,               

                                                                         АВ = ВС                                                                          BD бісектриса <B

                                                                         Довести:       

              А          D           С                                   <A = <С                                    

                                     

1. Розглянемо трикутник АВС  у якому BD бісектриса.

Розглянемо трикутники АВD  і СВD  у яких

ВD  спільна сторона АВ=ВС за умовою   і кут <ABD=<CBD 

Трикутники рівні за першою ознакою, тому рівні решту сторін і кутів. Отже   <A=<B 

AD=CD то BD- медіана

<BDA=<BDC а вони суміжні тому величина кожного 90  тоді

BD-висота    

                                

Теорему  доведено.

 

Записуємо у зошит

• Цікаво, а чи не має ця теорема наслідків?
• Так, вірно, адже, медіана, бісектриса і висота рівнобедреного трикутника, проведені до основи, збігаються.
• Давайте спробуємо сформулювати їх.

 

 

      А  тепер  давайте  перефразуємо  теорему про кути рівнобедреного трикутника, додавши  слово  якщо (відповідь  учнів)  і   поміняємо  місцями  умову  теореми  з  висновком. Яке  твердження  одержалось? (відповідь  учнів).

 

 

Це  твердження – теорема, обернена  до  попередньої  і  називається  ознакою  рівнобедреного  трикутника. Доведемо  її. Що  дано? (відповіді  учнів) Що  потрібно  довести? (відповіді  учнів)

Слайд 8.

 

 

 

Дано :                              В

трикутник АВС,                                1)  Розглянемо трикутники АВС і  СВА

 < A = < C                                            <A = <C, <C = <A,

Довести :                                              АС - спільна

АВ = ВС                 А              С      2)    АВС =     СВА  за  сторо-

                                                               ною  і  прилеглими  кутами

                                                            3) АВ = ВС  за  означенням

                                                                  рівних  трикутників.

Теорему  доведено.

 

 

 

Розв’язування вправ та задач

 

Робота з підручником.

Задача1

№12

Знайдіть кути при основі рівнобедреного трикутника, якщо кут між бічними сторонами дорівнює 72.

 

Задача 2

№ 25

Знайдіть кути рівнобедреного трикутника, якщо кут при його вершині у тричі більший за кут при основі.

 

Задача 3

№ 28

Знайдіть кути рівнобедреного трикутника, якщо зовнішній кут дорівнює 110  .

 

Задача 4

№29

У рівнобедреному трикутнику кут при вершині дорівнює 40. Знайдіть кут між основою і висотою, проведеною до бічної сторони.

 

Задача 5

№30

У рівнобедреному трикутнику кут між основою і висотою, проведеною до бічної сторони, дорівнює 25. Знайдіть кути трикутника.

 

 

 

                Рефлексія.

             Вправа «Незакінчені речення»

      «На сьогоднішньому уроці ми  дізналися…»

      «На сьогоднішньому уроці найважливішим відкриттям для мене було…»

      «На початку уроку я поставив (поставила) перед собою мету. Ось як я її    досягнув (досягнула)…»

 

 

 

 

Оголошення  оцінок.

Домашнє завдання.

Параграф 14

Задачі  ст 110 №28(2)   29(2)   ст. 109  №12 (2)

 

Теофіпільська ЗОШ І-ІІІ ст.

 

 

 

 

 

 

 

Конспект уроку

з геометрії у 7 класі

на тему:

«Властивості  й ознака рівнобедреного трикутника»

 

 

                                                  Вчитель: Зубик В.З.

 

 

 

 

 

2018