Контрольна робота №2. 7 клас. Геометрія. Суміжні та вертикальні кути
КР № 2 Суміжні та вертикальні кути
Варіант 1
1. Знайдіть градусну міру кута, якщо суміжний з ним кут дорівнює 37°.
|
а |
б |
в |
г |
|
37° |
180° |
143° |
137° |
2. Знайдіть невідомий кут х.
|
а |
б |
в |
г |
|
126° |
54° |
180° |
72° |
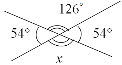
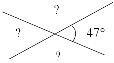
3. Знайдіть невідомі кути:
|
а |
б |
в |
г |
|
60°,60°,60° |
47°,47°, 133° |
47°,133°,133° |
45°,145°,145° |
4. Знайдіть вертикальні кути, якщо їх сума дорівнює 62°.
|
а |
б |
в |
г |
|
62° |
31° |
124° |
118° |
5. Установіть відповідність між кутами 1 – 3 та їх градусними мірами
(а –д), якщо ∠АМВ = 360, МR - бісектриса кута ВМD
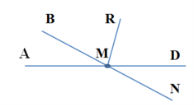 1. ∠NMD а) 1440
1. ∠NMD а) 1440
2. ∠AMN б) 1040
3. ∠BMR в) 720
г) 360
д) 1080
6. Знайдіть суміжні кути, якщо вони відносяться як 3:7.
7. Сума двох кутів, утворених при перетині двох прямих дорівнює 142°. Знайти ці кути.
8. З вершини заданого кута проведено промінь, перпендикулярний до його бісектриси. Цей промінь утворює з однією зі сторін заданого кута гострий кут, що дорівнює 300. Знайти величину заданого кута.
9. Кути DEF і MEF – суміжні, промінь EK – бісектриса ∠ DEF, ∠ KEF на 57° менший від ∠ MEF. Знайдіть кути DEF і MEF.
КР № 2 Суміжні та вертикальні кути
Варіант 2
1. Знайдіть градусну міру кута, якщо суміжний з ним кут дорівнює 115°.
|
а |
б |
в |
г |
|
115° |
180° |
65° |
135° |
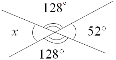
2. Знайдіть невідомий кут х.
|
а |
б |
в |
г |
|
128° |
76° |
180° |
52° |
|
а |
б |
в |
г |
|
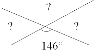
60°,60°,60° |
34°,146°,34° |
111°,69°,69° |
34°,146°,146° |
3. Знайдіть невідомі кути:
4. Знайдіть вертикальні кути, якщо їх сума дорівнює 74°.
|
а |
б |
в |
г |
|
106° |
74° |
37° |
148° |
5.Установіть відповідність між кутами 1 – 3 та їх градусними мірами
(а –д), якщо ∠АМВ = 480, МR - бісектриса кута ВМD
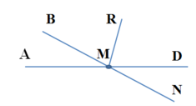 1. ∠NMD а) 1420
1. ∠NMD а) 1420
2. ∠AMN б) 1140
3. ∠BMR в) 660
г) 480
д) 1320
6. Знайдіть суміжні кути, якщо вони відносяться як 7:2.
7. Різниця двох кутів, утворених при перетині двох прямих дорівнює 42°. Знайти ці кути.
8. З вершини заданого кута проведено промінь, перпендикулярний до його бісектриси. Цей промінь утворює з однією зі сторін заданого кута гострий кут, що дорівнює 400. Знайти величину заданого кута.
9. Кути DАF і MАF – суміжні, промінь АK – бісектриса ∠ DАF, ∠ KАF у 4 рази менший від ∠ MАF. Знайдіть кути DАF і MАF.

про публікацію авторської розробки
Додати розробку
