Контрольна робота №3 «Об’єми многогранників» Варіант 1 1. Площа поверхні куба дорівнює 24 см2. Знайдіть об'єм куба. (З бали) 2. Знайдіть об'єм правильної чотирикутної піраміди, діагональ основи якої дорівнює 4 см, а бічне ребро утворює з площиною основи кут 45°. (З бали) 3. В основі прямої призми лежить ромб. Більша діагональ призми дорівнює d і нахилена до площини основи під кутом φ, а мен¬ша — утворює з бічним ребром кут α. Знайдіть об'єм призми. (З бали) 4. У правильній трикутній піраміді бічне ребро утворює з висотою кут α. Визначити об’єм піраміди, якщо відстань від середини висоти до бічного ребра дорівнює а. (З бали) Варіант 2 1. Об'єм куба дорівнює 125 см3. Знайдіть площу поверхні куба. (З бали) 2. Знайдіть об'єм правильної чотирикутної піраміди, діагональ основи якої дорівнює 8 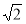см, а апофема піраміди дорівнює 5 см. (З бали) 3. В основі прямої призми лежить ромб з більшою діагоналлю d. Біль¬ша діагональ призми утворює з площиною основи кут γ, а мен¬ша — кут α. Знайдіть об'єм призми. (З бали) 4. У правильній трикутній піраміді висота утворює з площиною бічної грані кут β. Відстань від середини висоти до бічної грані дорівнює b. Визначити об’єм піраміди. (З бали) Контрольна робота №3 «Об’єми многогранників» Тести І рівень 1. Якщо об'єм куба дорівнює 64 см3, то площа його поверхні дорівнює: а) 4 см2; б) 16 см2; в) 32 см2; г) 96 см2. (1 бал) 2. Якщо площа основи трикутної піраміди дорівнює 3 см2, а висота — 3 см, то її об'єм дорівнює: а) 1 см3; б) 3 см3; в) 9 см3; г) 27 см3. (1 бал) 3. Якщо ребро куба збільшили у 2 рази, то його об'єм збільшиться в: а) 2 рази; б) 4 рази; в) 8 раз; г) 27 раз. (І бал) II рівень 1. Якщо сторони основ правильної чотирикутної призми збільшили в 2 рази, а висоту зменшили в 2 рази, то відношення об'єму одер¬жаної піраміди до об'єму даної становить: а) 4 :1; б) 2 :1; в) 1: 2 ; г) 1: 4 . (1 бал) 2. Якщо об'єм похилого паралелепіпеда з площею основи см2 і до¬вжиною бічного ребра 2 см дорівнює см3, то бічне ребро нахи¬лене до площини основи під кутом: а) 30°; б) arctg ; в) 45° ; г) arctg . (1 бал) 3. Якщо сторони основи правильної п-кутної піраміди зменшили в 3 рази (без зміни висоти), то її об'єм зменшився в: а) 3 рази; б) 3п раз; в) 9 раз; г) раз. (1 бал) III рівень 1. Якщо об'єм правильного тетраедра дорівнює 3 см3, то ребро тет¬раедра дорівнює: а) см; б) см; в) 6 см; г) 1 см. (2 бали) 2. Якщо бічне ребро правильної трикутної призми дорівнює висоті ос¬нови, а площа перерізу, проведеного через них, дорівнює Q, то об'¬єм призми дорівнює: а) ; б) ; в) ; г) . (2 бали) 3. Якщо висота правильної чотирикутної піраміди дорівнює H, а біч¬на грань утворює з основою кут α, то об'єм піраміди дорівнює: a) H3 tg2 α; б) H3 ctg2 α; в) H3 tg2 α; г) H3 ctg2 α. (2 бали) Відповідь. Варіант 1. 1. 8 см3; 2. см3; 3. d3 sin φ sin 2φ tg α; 4. Варіант 2. 1. 150 см2; 2. 64 см3; 3. d3 tg2 γ ctg α; 4. Таблиця відповідей Рівень Номер завдання Варіант 1 І 1 г 2 б 3 в II 1 б 2 а 3 в III 1 а 2 г 3 г