Контрольна робота "Логарифмічна функція"

11 клас (алгебра)

Контрольна робота № 2

Логарифмічна функція

Варіант 1

1. Значення виразу   log ₃ 27 + lg 10000 дорівнює:
     А) 0,0027;          Б) 7;          В) 12;           Г) 270000.

2. Областю визначення функції y = log ₇ ( 2x – 1 ) є:

     А) ( 2; + ∞ );     Б) ( – ∞; 2 );    В) ( 0,5; + ∞ );    Г) ( – ∞; 0,5 ).

3. Якщо log ₄ m  > log ₄ n, то виконується умова:
     А) m > n;     Б) m< n;     В) m = n;     Г) m  n.

4. Розв’яжіть рівняння:  а) log ₆ ( х - 2 ) = log ₆ 216;   б) log _х 125 = 3.

5. Розв’яжіть нерівність:  log ₈ ( 3x + 6 ) ≥ log ₈ ( 2 – x ).

6. Обчисліть:   .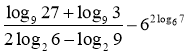  

7. Розв’яжіть рівняння: log _0,8 x + log _0,8 ( x – 1 ) = log _0,8 ( x + 3 ).

Примітка: Завдання 1, 2, 3 оцінюються по 1 балу, 4, 5, 6 - по 2 бали, 7 - 3 бали.

Варіант 2

1. Значення виразу log ₂ 16 + lg 1000 дорівнює:
     А) 0,016;          Б) 12;          В) 7;           Г) 16000.

2. Областю визначення функції y = log ₉ ( 4x – 1 ) є:

     А) ( – ∞; 0,25 );     Б) ( – ∞; 4 );    В) ( 4; + ∞ );    Г) ( 0,25; + ∞ ).  

3. Якщо log ₃ m < log ₃ n, то виконується умова:
    А) m > n;     Б) m < n;     В) m = n;     Г) m  n.

4. Розв’яжіть рівняння:  а) log ₇ ( х + 3 ) = log ₇ 49;   б) log _х 64 = 6.

5. Розв’яжіть нерівність:  log ₉ ( 3x – 4 )  ≤  log ₉ ( 5 – x ).

6. Обчисліть:   .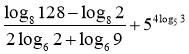

7. Розв’яжіть рівняння: log _0,4 x + log _0,4 ( x + 1 ) = log _0,4 ( 8 – x ).

Примітка: Завдання 1, 2, 3 оцінюються по 1 балу, 4, 5, 6 - по 2 бали, 7 - 3 бали.