Тема уроку: Найпростіші перетворення графіків функцій

Урок № 7

Тема уроку:   Найпростіші перетворення графіків функцій

Мета уроку.   Засвоєння учнями навичок та вмінь побудови графіків у=ах²+n

 у=а(х-m)² і  у=а(х-m)²+n; виконувати найпростіші перетворення графіків; формувати навички дослідження властивостей функцій; розвивати пам'ять, увагу, логічне мислення, культуру мовлення ; виховувати в учнів графічну культуру, наполегливість, самостійність, зосередженість, зацікавленість до предмета,  викликати в дітей інтерес до математики

Учні повинні: будувати, здійснювати перетворення графіків функцій, та виконувати нескладні дослідження.

Тип уроку: формування вмінь і навичок.

Структура уроку

 I.Перевірка домашнього завдання

 

II. Актуалізація опорних знань.

 

III. Формування вмінь і навичок розв’язувати вправи на    перетворення графіків функцій.

 

IV. Застосування знань, умінь та навичок  будувати графіки.

 

V.  Підсумок уроку

 

VI. Домашнє завдання

Хід уроку

                                                            «Графік – це лінія, що говорить, яка може багато про що розповісти»

М.Б.Балк

 

І. Перевірка домашнього завдання

             Усно. №303 ( ст.94 ). Відповідь: 3).

                       № 304  Відповідь: 1).

                       № 306  Відповідь: 1) III чверть;     3) II чверть;    

                                                       2) I  чверть;      4)  IV чверть.

                       № 308 Відповідь: 4).

(слайд №1-3)

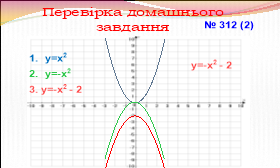
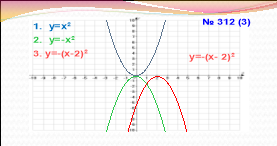
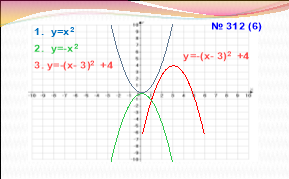
№ 312 (2;3;6) -  за записами, зробленими на мультимедійній дошці.

             Відповісти на запитання учнів, які виникли під час виконання домашнього завдання. 

(слайд № 4)

 

ІІ. Повідомлення теми та мети уроку. Актуалізація опорних знань.

(слайд № 5)

1. Як можна отримати графік функції y = f(x)+b, використовуючи графік      y = f(x)?

2. Яка фігура є графіком функції у=х² + b?

3. Які координати вершини параболи у = х²  + b?

4. Як можна отримати графік функції y = f(x+ a), використовуючи графік     y = f(x)?

5. Яка фігура є графіком функції у = (х+а)² ? 

6. Які координати вершини параболи   у = (х+а)² ? 

7. Яка фігура  є графіком функції    у = k ( х+а)²   + b, де k 0?    

(слайд № 6-16)

Визначте, графік якої функції зображено на малюнку, посилаючись на відповідні правила.

 

 

 

 

 

 

 

 

 

 

 

 

             

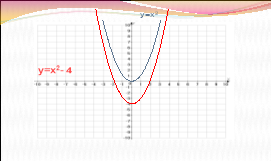
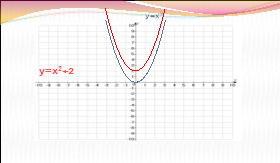
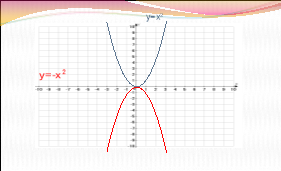
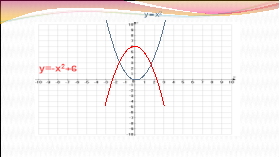
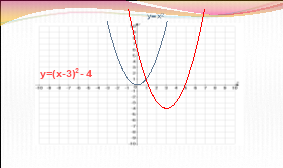
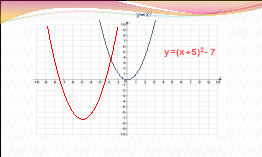
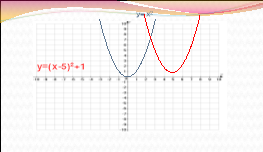
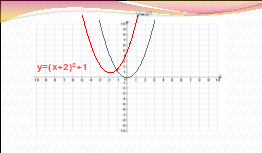
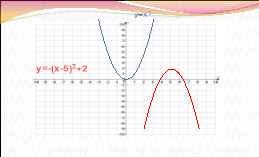
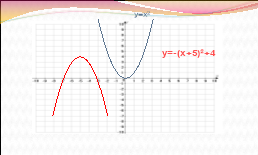
 ІІІ.Формування вмінь і навичок розв’язувати вправи на перетворення графіків функцій.

(слайд № 17-18)

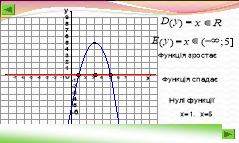
Опишіть властивості функції.

 

 

 

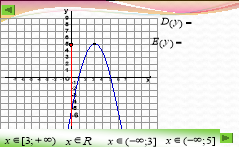
                                                Робота в парах.

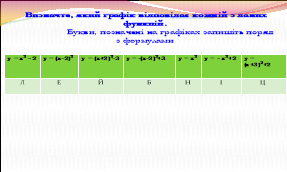
На рисунках зображено графіки функцій. Для кожного графіка вкажіть відповідну формулу.

Визначте, який графік відповідає кожній з даних функцій.

Букви, позначені на графіках запишіть поряд з формулами.

й	і
н	л
ц	е
б	к

 

(слайд № 19-20)

Визначте, який графік відповідає кожній з даних функцій.

 

 

y = x2 - 2	y = (x-2)2	y = (x+2)2-3	y = -(x-2)2+3	y = x2	y = - x2+2	y = (x+3)2+2
Л	Е	Й	Б	Н	І	Ц

 

                     Після виконання завдання учні коментують свій вибір.

                                       За правильне виконання (2 б)

                                                

(слайд № 21-27)

Виступ учня.

 

Історична довідка про Р. Декарта, П.Ферма, Г. Лейбніца, Л.Ейлора,  Больцано, Й Бернуллі  – видатних математиків, роботи яких відіграли значну роль у формуванні поняття функції

 

 

 

 

 

 

IV. Застосування знань, умінь та навичок  будувати графіки.

                                          Запитання до учнів.

                                           Колективна робота

Як побудувати графік функції y=x²+6x+9? Учитель пропонує скласти план побудови та побудувати даний графік в зошиті, один з учнів виконує завдання на дошці під керівництвом учителя.

Побудуйте графік  y=x²-8x+12. Користуючись графіком, знайдіть:

               а) область визначення функції;

               б) множину значень;

               б) нулі функції;

               в) проміжок зростання і проміжок спадання функції;

               г) при яких значеннях аргументу функція приймає додатних значень.

(слайд №  28-29)

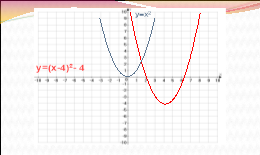
                         Самостійна робота навчального характеру.

 

 

(слайд №   30-31)

 

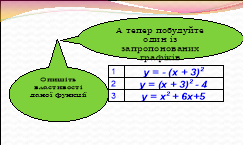
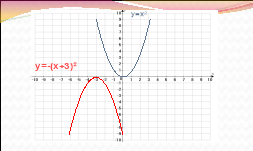
Побудуйте один з запропонованих графіків.

                                       а) y= - (x+3)²; (6 б)

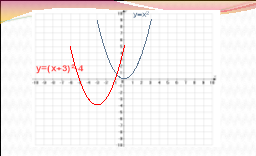
                                       б) y= (x+3)²-4;( 8 б)

                                       в) y=x²+6x+5. (10 б).              

                                   Дослідіть її властивості.

По закінченню роботи вчитель викликає до дошки по одному учню від кожної групи і пропонує відтворити завдання.

(слайд №  32-33)

 

 

V. Підсумок уроку

 Учитель аналізує роботу кожної групи учнів, нагадує, які перетворення графіків було виконано на цьому уроці. І підкреслює, що ці знання дуже важливі для вивчення наступних тем.

(слайд № 34)

Математичний диктант.

                                       Продовжіть  речення:

I - варіант II – варіант

 

1. Графіком функції y=4x² є ……              1. Графіком функції y=-0,4x² є …         

2. Вітки напрямлені ……                            2. Вітки напрямлені ……   

3. Область визначення …..                         3. Область визначення …..

4. Функція спадає ….                                  4. Функція зростає  ….                                  

(слайд № 35)

 

VI. Домашнє завдання § 2 п. 10 (А.Г. Мерзляк);  № 308-усно; №312(3;5); №317; №328(1).