Контрольна робота з алгебри та початків аналізу №6 з теми: "Тригонометричні формули"

Контрольна робота № 6

 з теми «Тригонометричні формули»

Варіант 1.

1. (1 б) Спростіть вираз:      
  А) -1;                    Б) 1;                        В) tg²;            Г) ctg² .

2. (1 б) Знайдіть значення виразу:  cos 34° ∙ cos26° -  sin34° ∙ sin26°.

   А) ;                    Б) ;                      В) ;               Г) 1 .
3. (2 б) Установіть відповідність між заданими виразами (1-4) та виразами,

    що їм тотожно дорівнюють (А-Д):

          1. cos ( – =                                А.          

          2. tg α ctg α =                                        Б. sin

          3. cos²α – sin²α =                                   В. 1

          4. 1 + ctg² =                                       Г. cos 2α

                                                                    Д. – sin .

4. (1 б) Спростіть вираз:  tg ( + ctg ( - .     

     А) tg²;             Б) - ctg² ;                  В) ctg² ;               Г) 1 .
 

5. (1 б)  Знайдіть значення sin 2α,

якщо відомо, що cos = і    < <   .
 

  6. (1 б)  Доведіть тотожність:  –    = tg 2.
 

7. (1 б)  Відомо, що sin α = , Знайдіть .

  8. (2 б) Спростіть вираз , якщо

  9. (2 б) Обчисліть: cos + cos + cos +…+ cos

Контрольна робота № 6

 з теми «Тригонометричні формули»

Варіант 2.

1. (1 б) Спростіть вираз:      . 

 А) 1;                        Б) -1;                          В) tg²;                   Г) ctg² .

2. (1 б)  Знайдіть значення виразу:  sin 38° ∙ cos52° +  cos 38° ∙ sin52°.

    А) ;                    Б) ;                         В) ;                      Г) 1 .

3. (1 б) Установіть відповідність між заданими виразами (1-4) та виразами,

    що їм тотожно дорівнюють (А-Д):

1. sin²α + cos²α =                                  А. tg (α – β)

2. =                                  Б. 1

3. 2 sin α cos α =                                   В. tg (α + β)

4. 1 + tg² =                                         Г. sin 2α

                                                              Д.    .

4. (1 б) Спростіть вираз:  cos ( + + sin ( + .     

      А) cos α + sin α;   Б) -2sin α;    В) cos α - sin α;    Г) 0 .

5. (1б) Знайдіть значення cos 2α,

якщо відомо, що sin = - і < < 2.

6. (1 б) Доведіть тотожність: +   = tg 2.

7. (1 б)  Відомо, що sin2α =– , Знайдіть 6sin

  8. (2 б) Спростіть вираз 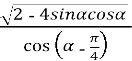, якщо

  9. (2 б) Обчисліть: cos + cos + cos +…+ cos