Контрольна робота з геометрії 10 клас "Паралельність прямих і площин у просторі"

Контрольна робота №2

Паралельність прямих і площин у просторі

Варіант 1

1. (0,5 б.) Укажіть правильне твердження:

А  Через три точки завжди можна провести безліч площин

Б  Через пряму і точку, яка не лежить на ній, можна провести дві різні площини

В  Через довільну пряму можна провести площину і до того ж тільки одну

Г  Через три точки можна провести одну або безліч площин

2. (0,5 б.) Укажіть правильне твердження:

А  Через дві мимобіжні прямі можна провести площину і до того ж тільки одну

Б  Якщо пряма перетинає одну з двох паралельних прямих, то вона обов’язково перетинає і другу

В  Якщо пряма a паралельна площині β, а пряма b лежить у площині β, то прямі а і  b мимобіжні

Г  Дві прямі, які паралельні третій прямій, - паралельні між собою

3. (1 б.) Яка з наведених фігур може бути паралельною проекцією рівнобічної трапеції?

4. (1 б.) Користуючись зображенням куба АВСDA₁B₁C₁D₁, вкажіть паралельні площини, які проведені через мимобіжні прямі АВ і СС₁.

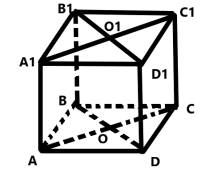А   (АВС) i (A₁D₁C₁)

Б  (DD₁C₁) i (AA₁B₁)

B  (A₁B₁C₁) i  (DD₁C₁)

Г  (АВС) i (AA₁B₁)

Д  (АA₁D₁) і (ВВ₁C₁)

5. (2 б.) У зображенні куба за площину проекцій взято площину АВСD, а проектуючоою прямою є пряма АA₁. Установіть відповідність між геометричними фігурами та їхніми паралельними проекціями.

6. (2 б.) Відрізок АВ та площина α паралельні між собою. Через кінці відрізка АВ проведено паралельні прямі. Пряма, що проходить через точку В перетинає площину α в точці В₁. Пряма, що проходить через точку А перетинає площину α в точці А₁.  1) Доведіть, що чотирикутник АВВ₁А₁ є паралелограмом. 2) Обчислити периметр паралелограма АВВ₁А₁, якщо АВ – ВВ₁=5см; АВ:ВВ₁=7:2.
7. (2 б.) Промінь КМ перетинає паралельні площини α і β в точках М₁ і М₂, а промінь КР – в точках Р₁ і Р₂ відповідно. Відомо, що М₁Р₁: М₂: Р₂=2:3. Обчисліть довжину відрізка М₁М₂, якщо КМ₁ = 8см.
8. (3б)Через точки В₁ і В₂, сторони АВ рівностороннього трикутника АВС проведено площини α і β, які паралельні прямій ВС. Обчисліть периметри фігур, на які розбивають цей трикутник дані площини, якщо АВ₁= В₁В₂= В₂В та АС=12см.

Контрольна робота №2

Паралельність прямих і площин у просторі

Варіант 2

1. (0,5 б.) Укажіть правильне твердження:

А  Через три точки завжди можна провести лише одну площину

Б  Якщо дві точки прямої належать площині, то пряма перетинає цю площину

В  Якщо А, В, С – спільні точки двох різних площин, то вони лежать на одній прямій

Г  Через три точки завжди можна провести безліч площин

2. (0,5 б.) Укажіть правильне твердження:

А  Якщо дві прямі не перетинаються, то вони паралельні

Б  Дві прямі, які паралельні третій, - мимобіжні між собою

В  Якщо пряма a паралельна площині β, а пряма b лежить у площині β, то прямі а і  b паралельні

Г  Площина і пряма, яка не лежить в цій площині, або не перетинаються, або перетинаються в одній точці

3. (1 б.) Яка з наведених фігур може бути паралельною проекцією правильного трикутника?

4. (1 б.) Користуючись зображенням куба АВСDA₁B₁C₁D₁, вкажіть паралельні площини, які проведені через мимобіжні прямі АВ і СС₁

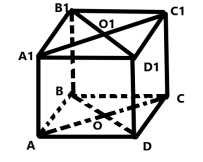А   (АВС) i (A₁D₁C₁)

Б  (DD₁C₁) i (AA₁B₁)

B  (A₁B₁C₁) i  (DD₁C₁)

Г  (АВС) i (AA₁B₁)

Д  (АA₁D₁) і (ВВ₁C₁)

5. (2 б.) У зображенні куба за площину проекцій взято площину АВСD, а проектуючоою прямою є пряма АA₁. Установіть відповідність між геометричними фігурами та їхніми паралельними проекціями.

6. (2 б.) Відрізок АВ та площина α паралельні між собою. Через кінці відрізка АВ проведено паралельні прямі. Пряма, що проходить через точку В перетинає площину α в точці В₁. Пряма, що проходить через точку А перетинає площину α в точці А₁.  1) Доведіть, що чотирикутник АВВ₁А₁ є паралелограмом. 2) Обчислити периметр паралелограма АВВ₁А₁, якщо ВВ₁ – АВ =8см; АВ:ВВ₁=3:4.
7. (2 б.) Промінь КМ перетинає паралельні площини α і β в точках М₁ і М₂, а промінь КР – в точках Р₁ і Р₂ відповідно. Відомо, що М₁Р₁: М₂: Р₂=2:3. Обчисліть довжину відрізка М₁М₂, якщо КМ₂ = 18см.
8. (3б)Через точки В₁ і В₂, сторони АВ рівностороннього трикутника АВС проведено площини α і β, які паралельні прямій ВС. Обчисліть периметри фігур, на які розбивають цей трикутник дані площини, якщо АВ₁= В₁В₂= В₂В та АС=18см.