Контрольна робота з геометрії для 11 класу по темі "Многогранники"

Контрольна робота № 1 за темою: «Многогранники»

І варіант

Початковий та середній рівні (6 балів)

1.               За якої з наведених умов чотирикутна призма є правильною?

2.               Кількість елементів куба дорівнює шести?

3.               Бічною гранню правильної чотирикутної призми є квадрат, площа якого дорівнює 36 см². Обчисліть периметр основи призми.

4.               У призмі площа основи дорівнює 12 см², а площа бічної поверхні – 60 см². Знайти площу повної поверхні призми.

5.               Знайдіть діагональ прямокутного паралелепіпеда, якщо його лінійні виміри дорівнюють 1 см, 3 см, 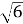см.

6.               У правильній піраміді бічне ребро дорівнює 10 см, а сторона основи – 12 см. Знайдіть апофему піраміди.

Достатній рівень (3 бали)

7.               Бічне ребро прямої трикутної призми дорівнює 7 см. Знайдіть площу повної поверхні призми, якщо її основа – прямокутний трикутник, гіпотенуза якого дорівнює

10 см, один із катетів – 6 см.

8.               Сторона основи прямокутного паралелепіпеда дорівнює 12 см, діагональ основи – 15 см, а висота – 3 см. Знайдіть:

1) площу діагонального перерізу паралелепіпеда;

2) площу повної поверхні паралелепіпеда.

Високий рівень (3 бали)

9. Основою прямого паралелепіпеда є ромб, площа якого  дорівнює 10 см². Знайдіть висоту паралелепіпеда, якщо площі його діагональних перерізів дорівнюють

15 см² і 12 см².

Контрольна робота № 2 за темою: «Многогранники»

ІІ варіант

Початковий та середній рівні (6 балів)

1.               В основі правильної трикутної піраміди лежить трикутник

2.       Скільки ребер у трикутній піраміді?

3.       Периметр основи правильної трикутної призми дорівнює 12 см. Обчисліть площу бічної грані, якщо відомо, що вона є квадратом.

4.        У призмі площа основи дорівнює 8 см², а площа повної поверхні – 40 см². Знайти площу бічної поверхні призми.

5.       Знайдіть діагональ прямокутного паралелепіпеда, якщо його лінійні виміри дорівнюють 3 см, 3 см, см.

6. Знайти площу бічної поверхні правильної чотирикутної піраміди, висота якої 12 см, якщо сторона основи – 10 см.

Достатній рівень (3 бали)

7.   Бічне ребро прямої чотирикутної призми дорівнює 5 см. Знайдіть площу повної поверхні призми, якщо її основа – прямокутник, діагональ якого дорівнює 10 см, а одна зі сторін – 8 см.

8. Сторони основи прямокутного паралелепіпеда дорівнюють 7 см і 24 см, а висота –

10 см. Знайдіть:

1) площу діагонального перерізу паралелепіпеда;

2) площу повної поверхні паралелепіпеда.

Високий рівень (3 бали)

9. Основою прямого паралелепіпеда є паралелограм з гострим кутом 30⁰ і площею 9 дм². Площі бічних граней паралелепіпеда дорівнюють 12 дм² і 24 дм². Знайдіть висоту паралелепіпеда.