Контрольна робота з математики для 10 класу: «Перпендикулярність прямих, прямих і площин, площин. Вимірювання відстаней і кутів у просторі»
Контрольна робота №2
«Перпендикулярність прямих, прямих і площин, площин.
Вимірювання відстаней і кутів у просторі» з математики (геометрії) рівня стандарт за новою програмою.
- робота № 3.docx docx
- робота № 3.pdf pdf
Контрольна робота №2
«Перпендикулярність прямих, прямих і площин, площин.
Вимірювання відстаней і кутів у просторі»
Варіант – 1
Оберіть правильний варіант відповіді:
-
 Точка А лежить поза площиною α. Скільки прямих, перпендикулярних до площини α, можна провести через точку А?
Точка А лежить поза площиною α. Скільки прямих, перпендикулярних до площини α, можна провести через точку А?
- Одну
- Дві
- Безліч
- Жодної
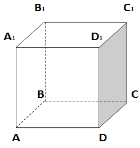
2. ABCDA1B1C1D1 – куб. Знайдіть градусну міру кута між прямими AC і DC1:
- 300;
- 450;
- 600;
- 900.
3. ABCDA1B1C1D1 – прямокутний паралелепіпед. Назвіть прямі, перпендикулярні до площини грані ABB1A1:
- DD1;
- CC1;
- ВС;
- DC
4. Дано прямі m i n та площину α, такі, що m||n, m┴α. Укажіть правильне твердження.
- Пряма n паралельна площині α.
- Пряма n перпендикулярна до площини α.
- Пряма n лежить у площині α.
- Пряма n перетинає площину α під кутом 450.
5. ABCDA1B1C1D1 – куб. Укажіть проекції відрізка B1D на площину ABCD:
- DB;
- AC;
- D1B1;
- A1C1
Встановіть відповідність:
6. Дано куб ABCDA1B1C1D1. Встановіть відповідність між твердженнями (1-4) та прямими (А-Д), для яких виконуються дані твердження:
- Паралельна прямій А B1
- Утворює з прямою А B1 кут 900
- Утворює з прямою А B1 кут 600
- Утворює з прямою А B1 кут 450
- A1D
- DC1
- DD1
- B1D
- D1C
Розв’яжіть задачу:
7. У кубі ABCDA1B1C1D1 знайдіть градусну міру кута між прямими AB1 і CD1.
Наведіть повне розв’язання до задачі:
8. Кінці відрізка, який не перетинає площину, віддалені від неї на 16 см і 24 см. Як віддалена від площини середина відрізка?
Варіант – 2
Оберіть правильний варіант відповіді:
1. Дано площину µ і точку S, яка належить цій площині. Скільки існує площин, які проходять через точку S і перпендикулярні до площини µ.
- Безліч
- Жодної
- Одна
- Одна або безліч
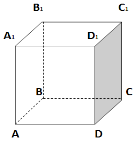 2 ABCDA1B1C1D1 – куб. Знайдіть градусну міру кута між прямими AC і В1D1:
2 ABCDA1B1C1D1 – куб. Знайдіть градусну міру кута між прямими AC і В1D1:
- 300;
- 450;
- 600;
- 900
3. ABCDA1B1C1D1 – прямокутний паралелепіпед. Назвіть прямі, перпендикулярні до площини грані ABCD:
- DD1;
- CC1;
- ВС;
- DC
4. Дано площини α i β та пряму b, таку, що b||α, b||β. Укажіть правильне твердження.
- Площини α паралельна площині β .
- Площини α перпендикулярна площині β .
- Площина α збігається з площиною β .
- Взаємне розташування площин α і β визначити неможливо .
5. ABCDA1B1C1D1 – куб. Укажіть проекції відрізка B1D на площину A1B1C1D1:
- DB;
- AC;
- D1B1;
- A1C1
Встановіть відповідність
6. Дано куб ABCDA1B1C1D1. Точка О1 – точка перетину діагоналей грані A1B1C1D1. Встановіть відповідність між твердженнями (1-4) та прямими (А-Д), для яких виконуються дані твердження:
- Паралельна площині (А ВС)
- Перпендикулярна до площини (А ВС)
- Утворює з площиною (А ВС) кут 450
-
Утворює з площиною (А ВС) кут
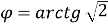
- B1D1
- A1С
- О1D
- CC1
- AB1
Розв’яжіть задачу:
7. У кубі ABCDA1B1C1D1 знайдіть градусну міру кута між прямими AС і ВС1.
Наведіть повне розв’язання до задачі:
8. Кінці відрізка, який не перетинає площину, віддалені від неї на 6 см і 14 см. Як віддалена від площини середина відрізка?
Оцінювання: завдання №1-5 по 1б. №6 –7 по 2бали, №8 – 3б.
Контрольна робота №2
«Перпендикулярність прямих, прямих і площин, площин. Вимірювання відстаней і кутів у просторі»
Варіант – 1 Оберіть правильний варіант відповіді:
1.
 Точка А лежить поза площиною α. Скільки прямих,
перпендикулярних до площини α, можна провести через точку А?
Точка А лежить поза площиною α. Скільки прямих,
перпендикулярних до площини α, можна провести через точку А?
А) Одну В) Безліч
Б) Дві Г) Жодної
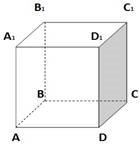
2. ABCDA1B1C1D1 – куб. Знайдіть градусну міру кута між прямими AC і DC1:
А) 300; В) 600; Б) 450; Г) 900.
3. ABCDA1B1C1D1 – прямокутний паралелепіпед. Назвіть прямі, перпендикулярні до площини грані ABB1A1:
А) DD1; В) ВС;
Б) CC1; Г) DC
4. Дано прямі m i n та площину α, такі, що m||n, m┴α. Укажіть правильне твердження.
А) Пряма n паралельна площині α.
Б) Пряма n перпендикулярна до площини α.
В) Пряма n лежить у площині α.
Г) Пряма n перетинає площину α під кутом 450.
5. ABCDA1B1C1D1 – куб. Укажіть проекції відрізка B1D на площину ABCD:
А) DB; В) D1B1;
Б) AC; Г) A1C1
Встановіть відповідність:
6. Дано куб ABCDA1B1C1D1. Встановіть відповідність між твердженнями (1-4) та прямими (А-Д), для яких виконуються дані твердження:
1) Паралельна прямій А B1 А) A1D 2) Утворює з прямою А B1 кут Б) DC1
900 В) DD1
3) Утворює з прямою А B1 кут Г) B1D
600 Д) D1C
4) Утворює з прямою А B1 кут
450 Розв’яжіть задачу:
7. У кубі ABCDA1B1C1D1 знайдіть градусну міру кута між прямими AB1 і CD1.
Наведіть повне розв’язання до задачі:
8. Кінці відрізка, який не перетинає площину, віддалені від неї на 16 см і 24 см. Як віддалена від площини середина відрізка?
Варіант – 2 Оберіть правильний варіант відповіді:
1. Дано площину µ і точку S, яка належить цій площині. Скільки існує площин, які проходять через точку S і перпендикулярні до площини µ.
А) Безліч В) Одна
Б) Жодної Г) Одна або безліч
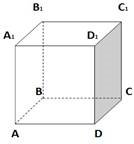 2 ABCDA1B1C1D1
– куб. Знайдіть градусну міру кута між прямими AC і В1D1:
2 ABCDA1B1C1D1
– куб. Знайдіть градусну міру кута між прямими AC і В1D1:
А) 300; В) 600;
Б) 450; Г) 900
3. ABCDA1B1C1D1 – прямокутний паралелепіпед.
Назвіть прямі, перпендикулярні до площини грані ABCD:
А) DD1; В) ВС;
Б) CC1; Г) DC
4. Дано площини α i β та пряму b, таку, що b||α, b||β. Укажіть правильне твердження.
А) Площини α паралельна площині β .
Б) Площини α перпендикулярна площині β .
В) Площина α збігається з площиною β .
Г) Взаємне розташування площин α і β визначити неможливо .
5. ABCDA1B1C1D1 – куб. Укажіть проекції відрізка B1D на площину A1B1C1D1:
А) DB; В) D1B1;
Б) AC; Г) A1C1
Встановіть відповідність
6. Дано куб ABCDA1B1C1D1. Точка О1 – точка перетину діагоналей грані A1B1C1D1. Встановіть відповідність між твердженнями (1-4) та прямими (АД), для яких виконуються дані твердження:
|
1) Паралельна площині (А ВС) 2) Перпендикулярна до площини (А ВС) 3) Утворює з площиною (А ВС) кут 450 4) Утворює з площиною (А ВС) |
А) B1D1 Б) A1С В) О1D Г) CC1 Д) AB1
|
![]()
кут 𝜑=𝑎𝑟𝑐𝑡𝑔 2 Розв’яжіть задачу:
7. У кубі ABCDA1B1C1D1 знайдіть градусну міру кута між прямими AС і
ВС1.
Наведіть повне розв’язання до задачі:
8. Кінці відрізка, який не перетинає площину, віддалені від неї на 6 см і 14 см. Як віддалена від площини середина відрізка?
Оцінювання: завдання №1-5 по 1б. №6 –7 по 2бали, №8 – 3б.


про публікацію авторської розробки
Додати розробку
