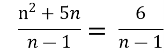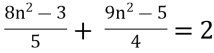Контрольна робота з теми «Квадратні рівняння. Теорема Вієта. Формули коренів квадратного рівняння»

Варіант 1

Варіант 2

1. (2 бали) Розв’язати рівняння:

А)  x² + 5x + 6 = 0;

Б) 5x² + 10x +15 = 0;

В) 2x² – 50 = 0;

Г) 3x² = 48;

Д) t² + 18t + 45 = 0.

А) 7y² - 35y + 42 = 0;

Б) 3y² + 24y + 21 = 0;
В) 3y² – 147 = 0;

Г) 2y² = 242;

Д) 6m² – 54m – 60 = 0.

2. (2 бали) При яких значеннях n виконується рівність:

А) (4n + 8)(2n + 6) = (3n + 7)²;

Б) .

А) 5(2n² – 2n) + 2(3n² + n) = 3;

Б) .

3. (2 бали) При якому значенні а число n буде коренем рівняння:

А) 8x² - аx + 8 = 0; n = 1

Б) x² + аx - 24 = 0; n= 2

А) 3x² – аx – 16 = 0;  n= -2

Б) 4x² – аx – 5 = 0; n= -1

4. (3 бали) Не обчислюючи коренів x₁ та x₂  рівняння

x² + 2x – 35 = 0,

x² + x – 12 = 0,

                                                                  знайдіть:

А) 4x₁² + 4x₂²;

Б) x₁³ + x₂³.

А) (x₁ – x₂)³;

Б) 5x₁ + 5x_2.

5. (3 бали)

Знайдіть значення k, при якому

один корінь рівняння

x² + (2k – 1)x + k² + 2 = 0

в двічі більший за інший.

5. (3 бали)

При якому значенні k, відношення коренів рівняння

x² + kx + k + 2 = 0

дорівнює 2?