Довідковий матеріал з теми "Квадратні корені. Дійсні числа"
Довідковий матеріал
з теми
«Квадратні корені. Дійсні числа»
(алгебра 8 клас)
1. Функція ![]() та її графік
та її графік
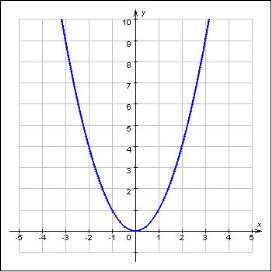
Графіком функції ![]() - є парабола, яка має дві нескінченні гілки, які плавно сходяться в одній точці.
- є парабола, яка має дві нескінченні гілки, які плавно сходяться в одній точці.
Властивості функції:
- область визначення – всі числа;
- область значень – всі невід’ємні числа;
-
додатні значення -
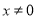 ;
;
- від’ємні значення – не має;
-
проміжки спадання -
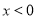 ;
;
-
проміжки зростання -
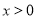 .
.
2. Арифметичний квадратний корінь
Арифметичним квадратним коренем з числа ![]() називається невід’ємне число, квадрат якого дорівнює
називається невід’ємне число, квадрат якого дорівнює ![]() .
.
Арифметичний квадратний корінь з числа ![]() позначають так:
позначають так: ![]() .
.
Знак ![]() називають знаком арифметичного квадратного кореня; вираз, який знаходиться під знаком кореня, називають підкореневим виразом. Запис
називають знаком арифметичного квадратного кореня; вираз, який знаходиться під знаком кореня, називають підкореневим виразом. Запис ![]() читають: «Квадратний корінь з числа
читають: «Квадратний корінь з числа ![]() ».
».
Наприклад:
![]() , так як 2 – число невід’ємне та
, так як 2 – число невід’ємне та ![]() ;
;
![]() , так як 1,1 – число невід’ємне та
, так як 1,1 – число невід’ємне та ![]() ;
;
![]() , так як 0 – число невід’ємне та
, так як 0 – число невід’ємне та ![]() .
.
Рівність ![]() є вірною, якщо виконується дві умови:
є вірною, якщо виконується дві умови:
![]()
![]()
Якщо ![]() вираз
вираз ![]() не має змісту, так як квадрат будь-якого числа невід’ємний.
не має змісту, так як квадрат будь-якого числа невід’ємний.
Наприклад:
вирази ![]() - не мають змісту.
- не мають змісту.
3. Тотожність ![]()
При будь-якому ![]() , при якому вираз
, при якому вираз ![]() має зміст, є вірним рівність
має зміст, є вірним рівність ![]()
Наприклад:
1) ![]() ;
;
2) ![]() .
.
4. Рівняння ![]()
Якщо ![]() , то рівняння
, то рівняння ![]() коренів немає. Дійсно, не існує числа, квадрат якого дорівнює від’ємному числу.
коренів немає. Дійсно, не існує числа, квадрат якого дорівнює від’ємному числу.
Якщо ![]() , то рівняння має єдиний корінь, який дорівнює нулю.
, то рівняння має єдиний корінь, який дорівнює нулю.
Якщо ![]() , то рівняння має два кореня.
, то рівняння має два кореня.
Наприклад:
рівняння ![]() має корені
має корені ![]() та
та ![]() , тобто
, тобто ![]() та
та ![]() ;
;
рівняння ![]() має корені
має корені ![]() та
та ![]() , тобто
, тобто ![]() та
та ![]() .
.
При будь-якому ![]() рівняння
рівняння ![]() має невід’ємний корінь
має невід’ємний корінь ![]() ; іншими словами, яке б число
; іншими словами, яке б число ![]() ми не взяли, знайдеться невід’ємне число, квадрат якого дорівнює
ми не взяли, знайдеться невід’ємне число, квадрат якого дорівнює ![]() . Це означає, що вираз
. Це означає, що вираз ![]() має зміст при будь-якому
має зміст при будь-якому ![]() .
.
5. Числові множини. Ірраціональні та дійсні числа
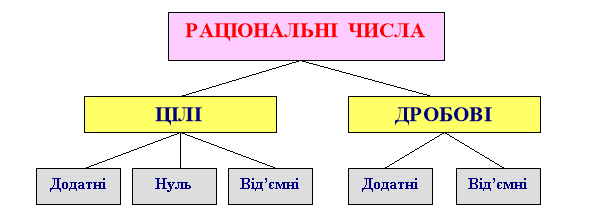

Кожне раціональне число можна уявити у вигляді нескінченного періодичного десяткового дробу; будь-який нескінченний періодичний десятковий дріб зображує деяке раціональне число.
Наприклад:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
6. Властивості арифметичного кореня
1. Корінь із добутку невід’ємних множників дорівнює добутку коренів з
цих множників
![]() та
та ![]() , то
, то ![]() .
.
- Корінь із дробу, чисельник якого невід’ємний, а знаменник додатній,
дорівнює кореню з чисельника, поділеному на корінь із знаменника
![]() та
та ![]() , то
, то ![]() .
.
-
Корінь із невід’ємного числа
 піднесеного до натурального степеня
піднесеного до натурального степеня 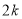 , дорівнює числу
, дорівнює числу 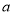 у натуральній степені
у натуральній степені 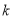
![]() .
.
Наприклад:
1) ![]() ;
;
2) ![]() ;
;
3) ![]() .
.
7. Тотожності ![]()
При будь-якому значенні ![]() є вірною рівність
є вірною рівність
![]()
Тотожність ![]() застосовується для добування квадратного кореня із степені з парним показником. Щоб добути корінь із степені з парним показником, достатньо уявити підкорінний вираз у вигляді квадрату деякого виразу і скористатися тотожністю
застосовується для добування квадратного кореня із степені з парним показником. Щоб добути корінь із степені з парним показником, достатньо уявити підкорінний вираз у вигляді квадрату деякого виразу і скористатися тотожністю ![]()
![]()
Наприклад:
1) ![]()
2) ![]() ;
;
3) ![]() .
.
8. Винесення множника за знак кореня
Якщо підкореневий вираз розкладається на множники, серед яких будуть такі, що з них можна добути квадратний корінь, то ці множники після добування з них кореня виходять з-під знаку кореня.
Наприклад:
1) ![]() ;
;
2) ![]() .
.
9. Внесення множника під знак кореня
При внесенні множника під знак квадратного кореня вони підносяться до квадрату та множаться на підкореневий вираз.
Наприклад:
1) ![]() ;
;
2) ![]() .
.
10. Звільнення від ірраціональності в знаменнику або чисельнику дробу
Алгоритм звільнення від ірраціональності в знаменнику або чисельнику дробу:
- розкласти на множники чисельник або знаменник дробу;
-
якщо чисельник або знаменник має вигляд
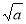 , або містить множник
, або містить множник 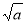 , то чисельник та знаменник необхідно помножити на
, то чисельник та знаменник необхідно помножити на 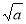 . Якщо знаменник або чисельник має вигляд
. Якщо знаменник або чисельник має вигляд 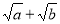 або
або 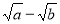 , або містить множник такого вигляду, то чисельник та знаменник необхідно помножити на
, або містить множник такого вигляду, то чисельник та знаменник необхідно помножити на 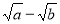 , або на
, або на 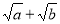 ;
;
- перетворити чисельник та знаменник дробу, якщо можливо, скоротити дріб.
Вирази вигляду ![]() та
та ![]() називаються спряженими.
називаються спряженими.
Наприклад:
1) ![]() ;
;
2) ![]() ;
;
3) 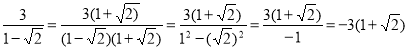 ;
;
4) 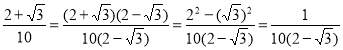 .
.
11. Функція ![]()
Властивості функції ![]() :
:
- область визначення – всі невід’ємні числа;
- область значень – всі невід’ємні числа;
-
додатні значення – всі числа, крім
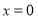 ;
;
- від’ємні значення – не має;
- проміжки спадання – не має;
-
проміжки зростання -
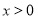 .
.
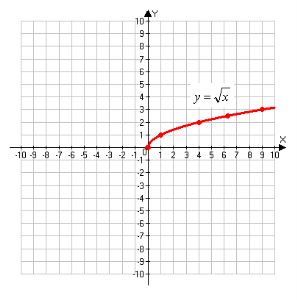
Графіком функції ![]() - є одна гілка параболи, яка виходить з початку координат.
- є одна гілка параболи, яка виходить з початку координат.
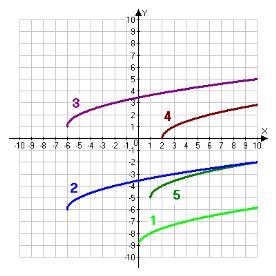 Наприклад:
Наприклад:

про публікацію авторської розробки
Додати розробку
