Контрольна робота за 1 семестр з математики 9 клас

Семестрова (І) контрольна з математики 

9 клас

Варіант 1 Початковий та середній рівень

1. (1б)Графік якої з наведених функцій отримаємо, якщо паралельно перенесемо графік функції y = x² уздовж осі абсцис на 4 одиниці вправо: а)y = x² + 4;       б)   y = x² − 4;        в) y = (x + 4)²;     г) y = (x − 4)².

  2   (0,5б) Який вигляд має теорема косинусів? А) c² a² b²2abcosC ;   Б) c² a² b²2abcosC ;   

В) c² a² b²2abcosC;   Г) c² a² b²2abcosC .

3.     (0,5б) Вкажіть формулу рівняння кола: 

А (xa)² (yb)² R          Б (xa)² (yb)² R²

В (xa)² (yb)² R²         Г (xa)² (yb)² R²

4.     (1б)Знайдіть область визначення функції    

                 а) (−∞; −5); б) (5; +∞);    в) (−∞; −5) ∪ (−5; +∞);     г) (−∞; +∞).

5   (1б)Оціни площу прямокутника зі сторонами 3 < a < 8; 2 < b < 3,5

а)  5 < S < 29;     б)  6 < S < 28;     в)  7 ≤ S ≤ 27;     г)  10 ≤ S ≤ 23.

6   .(1б)Знайдіть координати середини відрізка АВ, якщо А(- 6; 3), В(-2; -1).

А) (- 4 ; -2)              Б) (0; 3)       В) (- 6; 3)              Г) (-4; 1)

7.(1 бал) Знайдіть невідому сторону трикутника  МNK, якщо  МN = 5 см,   МК = 3√3  см,  < М = 30°. 

 А) 7 см;  Б) √7 см;   В) √97 см;  Г) 97 см. 

                                       Достатній рівень

8.(1,5б) Розв'яжіть систему нерівностей  ^,

9..(1,5б) Знайдіть значення х, при якому вектори а (х; 8) і b (- 25; 5):

а) колінеарні;                         б) перпендикулярні

Високий рівень

       10.(3б) Побудуйте графік функції  у = - х² - х + 2.

      Користуючись графіком, знайдіть:

1)  область значень функції;

2)  проміжки зростання і проміжки спадання функції;

Семестрова (І) контрольна з математики 

9 клас

Варіант ІІ Початковий та середній рівень

1.     (1б)Графік якої з наведених функцій отримаємо, якщо паралельно перенесемо графік функції y = x² уздовж осі ординат на 5 одиниці угору: а)y = x² + 5;       б)   y = x² − 5;        в) y = (x + 5)²;     г) y = (x − 5)².

2.  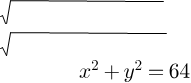   (0,5б) Вкажіть формулу відстані між двома точками: А AB (x₁ x₂)² (y₁ y₂)²     Б AB (x₁ x₂)² (y₁ y₂)²

В AB (x₁ x₂)(y₁ y₂)         Г AB (x₁ x₂)² (y₁ y₂)²

3.     (0,5б) Вкажіть радіус кола, заданого рівнянням           

А.32   Б . 8    В.16  Г.64

4.(1б)Знайдіть область визначення функції     

а) (−∞; −4); б) (4; +∞);    в) (−∞; 4) ∪ (4; +∞); г) (−∞; +∞).

5.(1б) Оціни площу прямокутника зі сторонами 2 < a < 5; 1,5 < b < 3

а)  6 < S < 7,5;     б)  7 ≤ S ≤ 16;     в)  3 < S < 15;     г)  4 ≤ S ≤ 16.

6.(1б) Знайдіть координати середини відрізка АВ, якщо А(- 6; 3), В(-2; -1).

А) (- 4 ; -2)              Б) (0; 3)       В) (- 6; 3)              Г) (-4; 1)

7     .(1 бал) Знайдіть довжину сторони АС  трикутника АВС, якщо АВ = 5 см, 

                 ВС = 3см,  < В= 60⁰.     А) 19 см;     Б) 49 см;      В) 7  см;     Г) √19  см.                                                               Достатній рівень

8     (1,5б) Розв'яжіть систему нерівностей^,

9     (1,5б)  Знайдіть значення y, при якому вектори m (-8; - 24) і n (12 ; y): 

                      а) колінеарні;                         б) перпендикулярні.

Високий рівень

   10.(3б) Побудуйте графік функції  у = х² - х - 6.

     Користуючись графіком, знайдіть:

1)  область значень функції;

2)  проміжки зростання і проміжки спадання функції;