Контрольная работа "Решение прямоугольных треугольников"

Контрольная работа

«Решение прямоугольных треугольников»

Вариант 1

Начальный уровень

3. Косинусом угла α называется отношение _____катета к________.

Средний уровень

4. Если катеты прямоугольного треугольника равны 5 и 12, то его гипотенуза равна:

а) 17;  б) 7;  в) 13;   г) другой ответ.

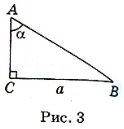5. Если в прямоугольном треугольнике АВС на рис. 3

(С=90°) ВС = а, А = α, то сторона АВ равна:

а) ; б) ; в) ;  г) .

6. Если гипотенуза  прямоугольного треугольника МNК (N=90°),  равна 25 см, один из катетов 15 см, то другой катет равен:

а) 10 см;  б) 35 см;  

в) 20 см;  г) другой ответ.

Достаточный уровень

7. Из точки к прямой проведены две наклонные, проекции которых на прямую равны 9 см и 16 см. Найдите расстояние от точки до прямой, если одна из наклонных на 5 см больше другой.

8. Диагональ равнобокой трапеции равна см и перпендикулярна к боковой стороне. Найдите периметр трапеции, если ее боковая сторона равна меньшему основанию и образует с большим основанием угол 60°.

Высокий уровень

9. В равнобедренном треугольнике угол при вершине, которая лежит против основания, равен α, а высота, проведенная к основанию, равна h. Найдите стороны треугольника.

Контрольная работа

«Решение прямоугольных треугольников»

Вариант 2

Начальный уровень

3. Синусом угла α называется отношение _____катета к________.

Средний уровень

4. Если катеты прямоугольного треугольника равны 7 и 24, то его гипотенуза равна:

а) 31;  б) 17;  в) 25;   г) другой ответ.

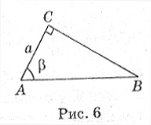
5. Если в прямоугольном треугольнике АВС на рис. 6  (С=90°) АС= а, А = β, то гипотенуза АВ равна:

а) ; б) ; в);  г).

6. Если гипотенуза  прямоугольного треугольника АВС (С=90°),  равна 41 см, один из катетов 40 см, то другой катет равен:

а) 1 см;  б) 9 см;  

в) 81 см;  г) другой ответ.

Достаточный уровень

7. Из точки к прямой проведены две наклонные, длины которых равны 13 см и 15 см. Найдите расстояние от точки до прямой, если разность проекций наклонных равна 4 см..

8. В прямоугольной трапеции АВСD (АD||ВС, А = α) ВD см,    АВD = СВD и ВDСD. Найдите периметр трапеции.

Высокий уровень

9. В равнобедренном треугольнике угол при основании равен β, а боковая сторона – b. Найдите основание и высоту, опущенную на основание треугольника.