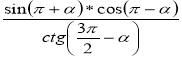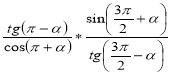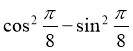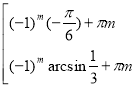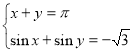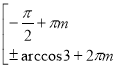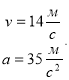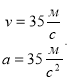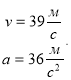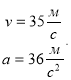Контрольні роботи у вигляді тестів для 10 класу

Про матеріал

Контрольні роботи – добре відома форма контролю знань учнів, яка дає можливість за короткий термін перевірити знання учнів усього класу. Результати контрольних робіт дають надійну інформацію про рівень засвоєння учнями нового матеріалу. За результатами учитель має можливість своєчасно заповнити прогалини в знаннях учнів.

Такі контрольні роботи дають можливість розкрити себе, учня, з будь-яким рівнем знань.

Перегляд файлу

Розробила вчитель математики

Пліщинської ЗОШ І-ІІІ ступенів

Ніщук Н.І.

ВАРІАНТ № 1

Завдання 1-10 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

(0,5 балів) Знайти значення виразу:

1); 2) ; 3) ; 4) 0.

2. (0,5 балів) Порівняйте з нулем вираз: sin 120⁰, cos 195⁰, ctg 359⁰.

Виберіть правильную серію відповідей:

1) + – – 2) – – + 3) + + – 4) + – +

3. (0,5 балів) Обчисліть

1) 12; 2) ; 3) 6; 4) 0.

У завданнях 4 – 6 спростити вираз

4. (0,5 балів)

1) – cos²; 2) cos²; 3) sin²; 4) – sin².

5. (1 бал) sin _* cos  _*ctg  – 1

1) 0; 2) cos²; 3) – sin²; 4) sin².

6. (1 бал)

1) sin  – cos ; 2) –2 ctg 2; 3) tg 2; 4) 0,5 ctg 2.

У завданнях 7 – 8 обчислити вираз (1,5 балів)

7. 2sin 15⁰_*cos 15⁰

1) ; 2) ; 3) ; 4) .

8. cos

1) ; 2) ; 3) ; 4) 0.

9. (2 бали) Дано: sin  = – где . Знайти tg 2

1) ; 2) ; 3) ; 4) .

10. (3 бали) Подати 105⁰ як 60⁰+ 45⁰, обчисліть sin 105⁰.

1) ; 2) ; 3) ; 4) .

КОНТРОЛЬНА РОБОТА. Тема. Тригонометричні функції

ВАРІАНТ № 2

Завдання 1-10 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

1. (0,5 балів) Знайти значення виразу:

1) 2,5; 2) 0,5; 3) ; 4) 1,5.

2. (0,5 балів) Порівняйте з нулем вираз: sin 187⁰, cos 215⁰, tg 80⁰.

Виберіть правильную серію відповідей:

1) + – – 2) – – + 3) + + – 4) + – +

3. (0,5 балів) Обчисліть

1) ; 2) -; 3) -; 4) .

У завданнях 4 – 6 спростити вираз

4. (0,5 балів)

1) tg²; 2) -tg²; 3) -ctg² ; 4) ctg².

5. (1 бал) :

1) – sin; 2) sin ; 3) – 2cos ; 4) sin – 2cos .

6. (1 бал)

1) ctg²; 2) tg²; 3) – tg²; 4) – ctg².

У завданнях 7 – 8 обчислити вираз (1,5 балів)

1) ; 2) ; 3) ; 4) 0.

8. cos150⁰

1) ; 2) ; 3) ; 4) .

9. (2 бали) Дано: cos  = – где . Знайти ctg 2

1) ; 2) ; 3) ; 4) .

10. (3 бали) Подати 15⁰ как 45⁰– 30⁰, обчислити cos 15⁰.

1) ; 2) ; 3) ; 4) .

КОНТРОЛЬНА РОБОТА. Тема. Тригонометричні рівняння та нерівності

ВАРІАНТ № 1

Завдання 1-8 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

1. (0,5 балів) Обчислити: arcsin () + 2arctg(-1)

1) ; 2) ; 3) ; 4) .

2. (0,5 балів) Обчислити: arcos () + 2arcctg()

1) ; 2) ; 3) ; 4) .

У завданнях 3,4. Розв’язати рівняння:

3. (0,5 балів) sin x -=0

1) 2); 3) 4)

4. (1 бал) cos 2x=1

1) 2) 3) 4)

5. (0,5 балів) Вказати рівняння, якому відповідає розвязок: :

1) tg x = 1; 2) cos x = 0; 3) sin x = -1; 4) ctg x =.

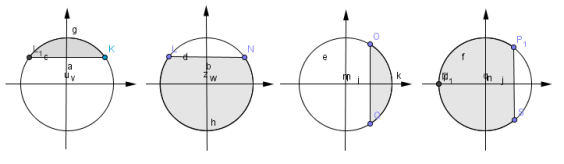
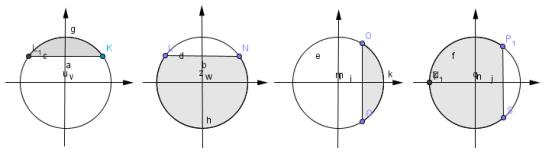
6. (1 бал) На якому з рисунків показано розв’язок нерівносі: cos x <?

1) 2) 3) 4)

У завданнях 7 – 9 розв’язати нерівність та рівняння

7. (1,5 балів) tg x ≥:

1) 2) 3) 4)

8. (1,5 балів) 6sin² x + sin x – 1 = 0

1) 2) 3) нет корней; 4) .

9. (2 бали) 2sin² x -sin 2x =0

10. (3 бали) Розв’язати систему рівнянь:

ВАРІАНТ № 2

Завдання 1-8 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

1. (0,5 балів) Обчислити: arcsin () + 0,5arctg (- )

1) ; 2) ; 3) ; 4) -.

2. (0,5 балів) Обчислити: arcos () + arcctg ()

1) ; 2) ; 3) ; 4)- .

У завданнях 3,4. Розв’язати рівняння:

3. (0,5 балів) sin x +=0

1) 2); 3) 4)

4. (1 бал) ctg (x+)=

1) 2) 3) 4)

5. (0,5 балів) Вказати рівняння, якому відповідає розвязок: :

1) ctg x = -1; 2) cos x = 0; 3) cos x = -1; 4) tg x = 1.

6. (1 бал) На якому з рисунків показано розв’язок нерівносі: sin x ≥?

1) 2) 3) 4)

У завданнях 7 – 9 розв’язати нерівність та рівняння

7. (1,5 балів) ctg x ≥

1) 2) 3) 4)

8. (1,5 балів) cos² x - 4sin x + 3 = 0

1) 2) 3) нет корней; 4) .

9. (2 бали) sin² x -3sin x cos x =0

10. (3 бали) Розв’язати систему рівнянь:

Контрольна работа. Тема: Властивості функцій.

ВАРІАНТ № 1

Завдання 1-11 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

(0,5 балів) Знайти область визначення функції

1) 2) 3) 4) .

2. (0,5 балів) Знайти область значень функції у = cos x +2

1) [-1;1]; 2)[-2;2]; 3) [0;2]; 4) [1;3].

3. (0,5 балів) Перевірити функцію на парність у = х⁴+ cos x

1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) інша відповідь.

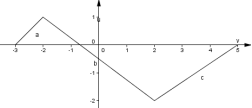
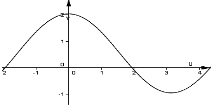
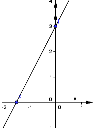
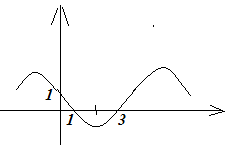
4. (0,5 балів) За графіком деякої функції у = f (x) знайти проміжки зростання

1) [-3;-2] U [2;5]; 2) [-3;5]; 3) [-2;2]; 4) [2;5].

5. (1 бал) Знайти нулі функції

1) 0; 2) 1; 3) 0; 1; 4) нет.

6. (1 бал) Знайти найменьший додатній період функції

1) π; 2) 2 π; 3) 0,5 π; 4) 4 π.

7. (1,5 балів) Знайти найменьше значення функції у = х² + 3х – 1

1) -1; 2) -3,25; 3) -1,5; 4) 1,25.

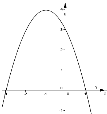
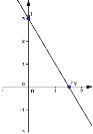
8. (1,5 балів) Вкажіть графік функції у = (х-1)²+4

1) 2) 3) 4)

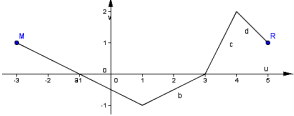
9. (1 бали) Знайти проміжки, на яких у>0

1) (-2;2); 2) [-2;0)U(2;4); 3) [-2;-1) U (2;4]; 4) [0;3].

10. (2 бали) Дано функцію f (x)= x³-2ax + 8 . Відомо, що f (1) = 5. Знайти f (-2).

1) 16; 2) 0; 3) 8; 4) -8.

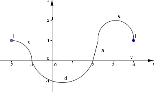
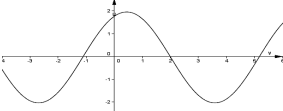
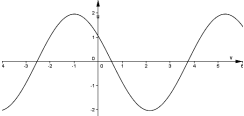
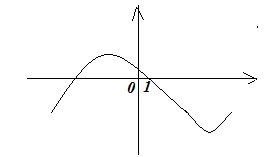
11. (2 бали) Вкажіть функцію, якій відповідає данний графік

1) ; 2) ; 3) ; 4) .

ВАРІАНТ № 2

Завдання 1-11 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

(0,5 балів) Знайти область визначення функції

1) 2) 3) 4) .

2. (0,5 балів) Знайти область значень функції у = sin x -2

1) [-1:1]; 2)[-3:-1]; 3) (-2;0); 4) [-2;2].

3. (0,5 балів) Перевірити функцію на парність

1) четная; 2) нечетная; 3) ни четная, ни нечетная; 4) інша відповідь.

4. (0,5 балів) За графіком деякої функції у = f (x) знайти проміжки зростання

1)[-2;3]U [2;4]; 2) [-3;5]; 3) [0;3]; 4) (-1;2).

5. (1 бал) Знайти нулі функції

1) 3; 2) -3; 3) 0; 4) -5.

6. (1 бал) Знайти найменьший додатній період функції у = tg 4x

1) 2π; 2); 3) 0,5 π; 4) 4 π.

7. (1,5 балів) Знайти найменьше значення функці у = -х² + 5х – 9

1) ; 2) -9; 3) 1,5; 4) 9,75.

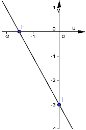
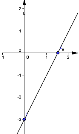
8. (1,5 балів) Вкажіть графік функції у = -2x-3

1) 2) 3) 4)

9. (1 бали) Знайти проміжки, на яких у<0

1) (-1;3); 2) [-3;1]U[4;5]; 3) (-3;-1); 4) [1;4].

10. (2 бали) Дано функцію f (x)= x³+5x - a . Відомо, що f (2) = 15. . Знайти f (-1).

1) -3; 2) -9; 3) -8; 4) 0.

11. (2 бали) Вкажіть функцію, якій відповідає данний графік

1) ; 2) ; 3) ; 4) .

Контрольна работа. Тема: Похідна. Застосування похідної.

ВАРІАНТ № 1

Завдання 1-7 мають тільки один правильний варіант відповіді. Оберіть цей варіант і запишіть його

1. (0,5 балів) Знайти похідну функції:

1) 2)

3) 4)

2. (0,5 балів) Знайти значення похідної функції в точці

1) 1; 2) 0; 3) 0,5; 4) -1.

3. (0,5 балів) Для якої з функцій знайдена похідна

1) 2) 3) 4)

4. (0,5 балів) Знайти значення кутового коефіцієнта дотичної, проведеної до графіка функції в точці з абсцисою

1) -3; 2) 0; 3) 3; 4) 5.

1) [-3;-2] U [2;5]; 2) [-3;5]; 3) [-2;2]; 4) [2;5].

5. (1 бал) Знайти , якщо sin

1) 2) 3) 4) 0.

6. (1 бал) Напишіть рівняння дотичної до графіка функції в точці

з абсцисою

1) у = - 3х – 3; 2) у = 8х+13; 3) у = - 8х – 3; 4) у = - 8х +13.

7. (1,5 балів) . Знайти швидкість та прискорення точки в момент часу c., якщо вона рухається прямолінійно за законом (координата вимірюється в метрах).