Тема уроку. Розв’язування ірраціональних рівнянь

Алгебра і початки аналізу 10 клас

Тема уроку. Розв’язування ірраціональних рівнянь

Мета уроку. Удосконалювати навички розв’язування ірраціональних рівнянь різними способами; спрямувати діяльність на встановлення зв’язків між цими способами; сприяти розвитку творчих здібностей учнів, вмінню шукати легші, ефективніші способи.

Очікувані результати: учні повинні вміти розв'язувати нескладні ірраціональні рівняння.

Основні поняття: ірраціональні рівняння, сторонній корінь.

Компетентності, що формуються: математична – уміння оперувати числовою інформацією, уміння розв’язувати нескладні ірраціональні рівняння; ключові – інформаційно-цифрова; соціальна і громадянська; спілкування державною мовою; вміння вчитися впродовж життя та творчо застосовувати набуті знання.

Обладнання: підручник, посібник «Алгебра у таблицях», 10 клас, Роєва Т.Г.

Тип уроку. Узагальнення знань, умінь, навичок.

ХІД УРОКУ

Вчитель. Систематизацію відомостей про способи розв’язування ірраціональних рівнянь доцільно провести, розв’язуючи конкретне ірраціональне рівняння.

 Скористаємося посібником «Алгебра у таблицях», 10 клас, Роєва Т.Г. і повторимо основні поняття про ірраціональні рівняння та основні методи розв’язування ірраціональних рівнянь.(Читання по фразах і коротке обговорення його змісту).

В процесі розв'язування рівнянь зосередьте свою увагу на тому:

Чому при піднесенні обох частин рівняння до парного степеня можуть з'явитися сторонні корені? Як відсіюють сторонні корені?

 Розв’язати рівняння  (1)

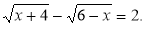
Спосіб 1.

Піднесемо до квадрата обидві частини цього рівняння:

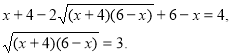
Піднесемо знову до квадрата обидві частини останнього рівняння і зведемо подібні члени. Отримаємо:   

 Перевіркою встановлено, що є коренем рівняння.

Спосіб 2.

Запишемо рівняння (1) у вигляді: 

Піднесемо до квадрата обидві частини цього рівняння. Отримаємо

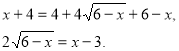
Знову піднесемо до квадрата. Отримаємо

Знову робимо перевірку і встановлюємо, що коренем рівняння є

 Робимо порівняння даних способів, вказуючи на те, що при розв’язуванні ірраціональних рівнянь методом піднесення обох частин рівняння до одного і того самого степеня раціональнішим є другий спосіб, при якому проводиться локалізація одного із радикалів, що спрощує тотожні перетворення.

 Крім того, нагадаємо учням, що при піднесенні до парного степеня отримаємо в загальному випадку рівняння нерівносильне даному, а тому перевірка знайдених значень невідомого за умовою даного рівняння є обов’язковою, тобто вона є складовою частиною розв’язування. Розв’язуючи рівняння даним методом, наголошуємо, що відшукання ОДЗ не є обов’язковим тому, що:

по-перше, вимагається розв’язати рівняння, а для нього не обов’язково шукати ОДЗ;

по-друге, отриманий корінь може належати ОДЗ, але бути стороннім, що можна проілюструвати і при розв’язуванні даного рівняння, ОДЗ якого . Тобто корінь х=-3,хоч і належить ОДЗ, але є стороннім.

Спосіб 3. Метод рівносильних перетворень.

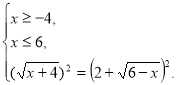
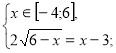
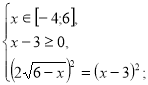
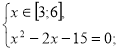
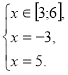
Звідки х=5. Перевірка не потрібна.

Учням обов’язково слід наголосити, що даний метод:

1. не розв’язуючи рівняння, в деяких випадках дає змогу встановити, що воно не має дійсних коренів;
2. не потребує безпосередньої перевірки коренів, що робить його ефективнішим на відміну від попереднього методу, коли перевірка ускладнена;
3. інколи потребує громіздких тотожних перетворень.

Спосіб 4. Метод введення допоміжних змінних.

Нехай тоді І нарешті отримуємо:

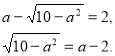
Розв’язавши останнє рівняння одним із попередніх методів, отримуємо, що

а=3, а отже, х=5.

Спосіб 5. Графічний.

Побудувавши графіки функцій і  , знайдемо корінь рівняння х=5.

Підсумок уроку. Чому при піднесенні обох частин рівняння до парного степеня можуть з'явитися сторонні корені? Як відсіюють сторонні корені?

Домашнє завдання. Попрацювати над пошуками інших способів розв’язування даного рівняння.

Підказка. 1) метод домноження на спряжений вираз.

                 2) метод використання властивості функції.

                 3) Підбором нескладно знайти корінь рівняння.