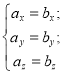Координати і вектори у просторі
1
ТЕМА : Декартові координати в просторі. Відстань між точками та координати середини відрізка. Вектори в просторі, рівні вектори, компланарні вектори. Дії з векторами та їх властивості.
1. Декартові координати в просторі
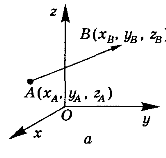
Візьмемо три взаємноперпендикулярніпряміOх, Oy, Oz, якіперетинаються в однійточціО (див.рисунок).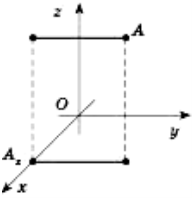
Проведемо через кожну пару цихпрямихплощину. Площина, яка проходить через пряміOх і Oу, називаєтьсяплощиноюOxy. ДвііншіплощининазиваютьсявідповідноOxzіOyz.
ПряміOx, Oy, Ozназиваютьсякоординатними осями (Ox — вісьабсцис, Oy — вісь ординат, Oz— вісьаплікат).
Точка їхперетинуО — початок координат,
площини Oxy, Oxz,Oyz — координатні площини.
Точка О розбиваєкожну з осей координат на двіпівпрямі — півосі.Домовимось одну пів ось називати додатною, а другу — від’ємною.Візьмемо тепер довільну точку А й проведемo через не їплощину, паралельну площині Oyz. Вона перетинаєвісь Ox у деякій точці![]() . Координатою х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка
. Координатою х точки А називається число, яке дорівнює за абсолютною величиною довжині відрізка![]() . Це число додатне, якщо точка
. Це число додатне, якщо точка ![]() лежить на додатній півосі Оx, івід’ємне, якщо точка
лежить на додатній півосі Оx, івід’ємне, якщо точка ![]() лежить на від’ємній півосі.
лежить на від’ємній півосі.
Якщо точка ![]() збігається з точкоюО, то вважаємо, що
збігається з точкоюО, то вважаємо, що![]() . Аналогічно означаємо координати y і z точки A. Координати точки записуватимемо в дужках поряд із буквеним позначенням точки:
. Аналогічно означаємо координати y і z точки A. Координати точки записуватимемо в дужках поряд із буквеним позначенням точки: ![]() .
.
Якщо точка A не належить жодній із координатних площин, то ц іплощини разом із трьома паралельними їм площинами, як і проходять через точкуА, обмежують прямокутний паралелепіпед.
Звернітьувагу на таке.
1) ![]() осі Oх;
осі Oх;
![]() осіOу;
осіOу;
![]() осіOz (див.рисунок).
осіOz (див.рисунок).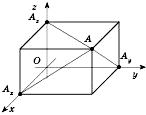
2)
|
Точка лежить на осі |
Ox |
Oy |
Oz |
|
Її координати |
(x;0; 0) |
(0;y; 0) |
(0;0; z) |
|
|
|
|
|
|
Точка лежить на площині |
Oxy |
Oyz |
Oxz |
|
Їїкоординати |
(x;y;0) |
(0; y;z) |
(x;0;z) |
2. Відстань між точками та координати середини відрізка.
Для знаходження відстані між двома точками ![]() користуються формулою
користуються формулою ![]()
Наприклад: Знайдіть відстань АВ, якщо А(-1; 3; -1), В(-1; 0; - 5).
Розв’язання
![]()
Відповідь.АВ=5
Наприклад:Знайти точку, яка знаходиться на однаковій відстані від трьох даних точок М1(1;2), М2(-1;-2), М3(2;-5).
Розв’язання
Позначимо шукану точку через М(х; у), тоді М1М = М2М = М3М.
За формулою відстані між двома точками:
![]()
Отже, 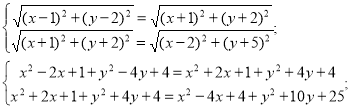
![]()
Нехай ![]() – середина відрізка
– середина відрізка ![]() де
де ![]() . Тоді
. Тоді ![]()
Наприклад: Які координати середини С відрізка АВ, якщо А(0; 2; -11), В (2; 0; -1)?
Розв’язання
![]()
Відповідь. С(1;1;-6).
- Вектори в просторі, рівні вектори, колінеарні вектори, компланарні вектори. Дії над векторами.
Вектором називається напрямлений відрізок. Напрям відрізка вказується стрілкою. Позначають вектор або двома великими літерами зі стрілкою (іноді з рискою) над ними, або однією маленькою літерою зі стрілкою.
Два вектора називаються рівними між собою, якщо кожний із них можна дістати паралельним перенесенням іншого. Рівні вектори є паралельними (колінеарними), мають один і той самий напрям і однакову довжину. У колінеарних векторів відповідні координати пропорційні. Довжина вектора ![]() називається абсолютною величиною або модулем вектора і позначається
називається абсолютною величиною або модулем вектора і позначається ![]() .
.
Вектори в просторі
|
|
|
|
Координати вектора (рис. а)
|
Довжина вектора
|
|
Рівність векторів
|
|
|
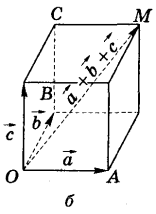
Сума векторів (рис. б)
|
|
|
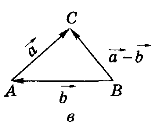
Різниця векторів (рис. в)
|
|
Добуток вектора на число
λ· |
|
Колінеарні вектори
|
|
![]()
![]()


про публікацію авторської розробки
Додати розробку