Тема уроку.   Координати середини відрізка.

Мета уроку: виведення формул для знаходження координат середини відрізка та застосування цих формул до розв'язування задач.

Обладнання: схема «Координати середини відрізка».

Хід уроку

І. Перевірка домашнього завдання

1. Відповісти на запитання, які виникли в учнів при виконанні задач № 4, 6, 7.

2. Самостійна робота.

Варіант 1

1) Знайдіть відстань між точками А(-1; 0; 2) і В (1; -2; 3). (5 балів)

2) Знайдіть на осі х точки, які віддалені від точки А (4; - 2; 3) на від­стань 7. (7 балів)

Варіант 2

1) Знайдіть відстань між точками А (2; 3; 1) і В (1; 1; -1). (5 балів)

2) Знайдіть на осі у точки, які віддалені від точки А(-3; 2; 4) на від­стань 13. (7 балів)

Варіант З

1) Знайдіть відстань між точками А(-1; - 2; 3) і В (-2; 0; 1). (5 балів)

2) Знайдіть на осі г точки, які віддалені від точки А(3; -4; 6) на від­стань 13. (7 балів)

Варіант 4

1) Знайдіть відстань між точками А (-2; -3; 1) і В(-1; - 1; 3). (5 балів)

2) Знайдіть на осі z точки, які віддалені від точки А (-2; 3; 4) на від­стань 7.  (7 балів)

Відповідь.  Варіант 1. 1) 3; 2) (10; 0; 0) і (-2; 0; 0).

Варіант 2. 1) 3; 2) (0; 14; 0) і (0;-10;0).

Варіант 3. 1) 3; 2) (0; 0; 18) і (0;0;-6).

Варіант 4. 1) 3; 2) (0;0;-2) і (0; 0; 10).

II. Сприйняття й усвідомлення нового матеріалу

Розв'язування задач

Знайдіть координату середини відрізка АВ, якщо:

а) А(5) і В(9); б) А(-3) і В(7);  в)А(а) і В(b).

Знайдіть координати середини відрізка АВ, якщо:

а) А(3;2) і B(1; 4);   б) A(x_A ; y_A) і В(х_B ; у_B).

Формули для координат середини відрізка, якщо задано координати його кінців.

Твердження.

Кожна координата середини відрізка дорівнює півсумі від­повідних координат його кінців.

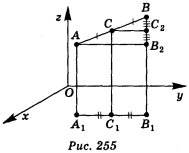
Доведення

Нехай А (х_A; у_A; z_A) і В(х_B; у_B; z_B) — дві довільні точки простору. Вира­зимо координати середини С відрізка АВ через координати його кінців А і В (рис. 255). Через точки А, В, С проведе­мо прямі, паралельні осі z, які перетнуть площину ху в точках         А₁(х_A, у_A, 0), B₁ (х_B, у_B, 0), С₁(x_C, у_C, 0) відповідно. Відомо, що в координатній площині координати середини відрізка виража­ються через координати його кінців за формулами: ; .

Провівши АА₂ || А₁B₁ і СС₂ || А₁В₁, матимемо: .

Розв'язування задач

1. Які координати середини С відрізка АВ, якщо А(0; 2; -11), В (2; 0; -1)? (Відповідь. С(1;1;-6).)
2. Дано С(2; 6; 3), А(4; 2; 1). Знайдіть координати точки В, якщо ві­домо, що  АС = ВС і точки А, В, С лежать на одній прямій. (Відповідь. В(0;10;5).)
3. Знайдіть координати середин сторін трикутника АВС, якщо А(2; 0; 2), В(2;2;0), С(2;2;2). (Відповідь. A₁(2; 2; 1), B₁(2; 1; 2), C₁(2; 1; 1).)
4. Знайдіть довжину медіани AM трикутника АВС, якщо А (2; 1; 3), В(2; 1; 5), С(0; 1; 1). (Відповідь. AM = 1.)
5. Задача № 9 із підручника (с. 55).
6. Задача № 13 (3) із підручника (с. 55)
7. Задача № 15 із підручника (с. 55).
8. Точки М(-2; 3; 4), N(3; 5; 2) і К(3; -5; 1) — середини сторін три­кутника. Знайдіть координати вершин цього трикутника.

(Відповідь. (-2; -7; 3), (-2; -13; 5), (8; -3; -1).)

9. Якщо А (х_A; у_A; z_A), В(х_B; у_B; z_B)  C (х_C; у_C; z_C)  — координати вершин трикутника, то М 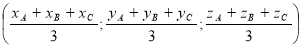– точка перетину медіан трикутника. Довести.

III. Домашнє завдання

§ 4, п. 25; контрольне запитання № 3; задачі № 10 (1), 11 (1), 12, 13 (1) (с. 55).

IV. Підведення підсумку уроку

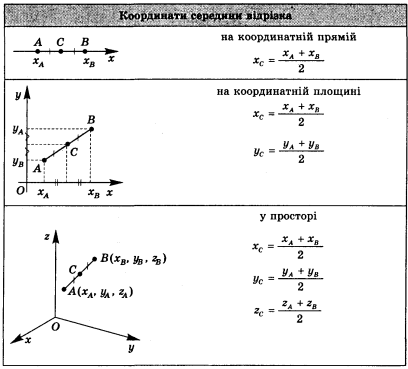При підведенні підсумку уроку можна скористатися даною стінною таблицею.

Запитання до класу

1. Як знайти координату середини відрізка, кінці якого лежать на ко­ординатній прямій?
2. Як знайти координати середини відрізка, кінці якого лежать у ко­ординатній площині?
3. Як знайти координати середини відрізка, заданого в просторі?