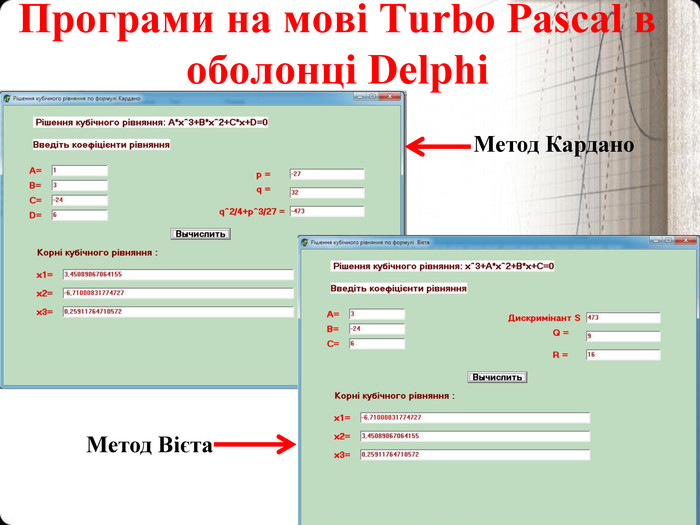
Кубічні рівняння. Метод Кардано. Метод Вієта
- рівняння.doc doc
- суперечка.ppt ppt
1



2018 рік
Зміст:
Методи розв’язування кубічних рівнянь
ВВЕДЕННЯ
Когда куб рядом с вещью
Вместе равны какому-либо числу,
То найди два других числа,
На него разнящихся,
Потом допусти и всегда держись
Этого правила, что их произведение
Должно равняться кубу третьей вещи.
Возьми от них стороны куба
И правильно вычти их.
Остаток даст тебе искомую вещь…
Нікколо Тарталья
Не всяке рівняння у результаті перетворень або за допомогою вдалої заміни змінної може бути зведене до рівняння того або іншого стандартного виду, для якого існує певний алгоритм рішення. У таких випадках іноді виявляється корисним використовувати інші методи рішення. Об'єкт дослідження - рівняння, що не піддаються рішенню за допомогою стандартних методів, або що відрізняються громіздкістю стандартного рішення.
Метою даної роботи є ознайомлення з нестандартними методами рішення рівнянь.
Для досягнення поставленої мети в даній роботі вирішувалися наступні задачі:
- зібрати відомості з історії математики про рішення рівнянь;
- розглянути й застосувати на практиці додаткові нестандартні методи рішення рівнянь.
Практична значимість роботи полягає в тому, що не завжди при рішенні складних рівнянь варто йти по «протоптаною стежкою», намагаючись знайти рішення «у чоло», досить лише глянути на нього й знайти зачіпку, що дозволяє уникнути складних обчислень і перетворень.
Історичні відомості
Диспути в 14-15 столітті завжди представляли собою цікаве видовище, що приваблювали городян від малого до великого. Теми диспутів носили різноманітний характер, але обов'язково науковий. При цьому під наукою розуміли те, що входило до переліку так званих «семи вільних мистецтв» було, звичайно, і богослов'я. Богословські диспути були найбільш частими. Сперечалися про все. Наприклад : про те, чи долучати мишу до духу святого, якщо з'їсть причастя, чи могла Кумськая сивилла передбачити народження Ісуса Христа, чому брати і сестри рятівника не зараховані до лику святих і т. д.
Про суперечку, яка повинна була відбутися між прославленим математиком і не менш прославленим лікарем, висловлювалися лише найзагальніші здогади, так як ніхто нічого не знав. Говорили, що один з них обдурив іншого ( хто саме і кого саме невідомо) . Майже всі ті , хто зібралися на площі мали про математику недалекі уявлення , але кожен з нетерпінням чекав початку диспуту . Це завжди було цікаво , можна було посміятися над невдахою , незалежно від того , правий він чи ні.
Коли годинник на ратуші пробив п'ять , ворота широко відчинилися і натовп кинувся всередину собору. По обидві сторони від осьової лінії, що з'єднує вхід з вівтарем , у двох бічних колон були споруджені дві високі кафедри , призначені для сперечальників . Присутні голосно шуміли , не звертаючи ніякої уваги на те , що знаходилися в церкві. Нарешті , перед залізними гратами , відділяла іконостас від решти частини центрального нефа , з'явився міський глашатай в чорно- фіолетовому плащі і проголосив : « Славетні громадяни міста Мілана ! Зараз перед вами виступить знаменитий математик Нікколо Тарталья. Його противником мав бути математик і лікар Джеронімо Кардано. Нікколо Тарталья звинувачує Кардано в тому , що останній у своїй книзі «Ars magna» опублікував спосіб розв’язку рівняння 3-го ступеня , що належить йому, Тарталье. Однак сам Кардано на диспут прийти не зміг і тому прислав свого учня Луїджі Феррарі. Отже, диспут оголошується відкритим , учасники його запрошуються на кафедри». На ліву від входу кафедру піднявся незграбний чоловік з горбатим носом і кучерявою бородою, а на протилежну кафедру зійшов молодий чоловік двадцяти з невеликим років, з красивим самовпевненим обличчям. У всій його манері триматися позначалася повна впевненість у тому , що кожен його жест і кожне його слово будуть прийняті із захопленням.
Почав Тарталья :
« Шановні панове! Вам відомо , що 13 років тому мені вдалося знайти спосіб рішення рівняння 3-го ступеня і тоді я , користуючись цим способом , здобув перемогу в диспуті з Фіорі . Мій спосіб привернув увагу вашого співгромадянина Кардано і він доклав усе своє хитромудре мистецтво, щоб вивідати у мене секрет . Він не зупинився ні перед обманом , ні перед прямим підробкою. Ви знаєте також , що 3 роки тому в Нюрнберзі вийшла книга Кардано про правила алгебри , де мій спосіб , так безсовісно викрадений , був зроблений надбанням кожного. Я викликав Кардано і його учня на змагання. Я запропонував вирішити 31 завдання , стільки ж було запропоновано і мені моїми супротивниками. Був визначений термін для вирішення завдань - 15 днів . Мені вдалося за 7 днів вирішити більшу частину тих завдань , які були складені Кардано і Феррарі . Я надрукував їх і послав з кур'єром в Мілан . Однак мені довелося чекати цілих п'ять місяців , поки я отримав відповіді до своїх завдань . Вони були вирішені не правильно . Це і дало мені підставу викликати обох на публічний диспут». Тарталья замовк. Молода людина , подивившись на нещасного Тарталью вимовив:
«Шановні панове! Мій гідний супротивник дозволив собі в перших же словах свого виступу висловити стільки наклепу на мою адресу і на адресу мого вчителя , його аргументація була настільки голослівною , що мені навряд чи доставить, яка не - будь праця спростувати перше і показати вам неспроможність другого . Насамперед , про який обман може йти мова , якщо Нікколо Тарталья абсолютно добровільно поділився своїм способом з нами обома? І ось як пише Джеронімо Кардано про роль мого супротивника у відкритті алгебраїчного правила . Він каже « що не йому , Кардано, а моєму другові Тарталье належить честь відкриття такого прекрасного і дивного , що перевершує людське дотепність і всі таланти людського духу. Це відкриття є по істині небесний дар , таке прекрасне доказ сили розуму , його осягнути , що вже ніщо, не може вважатися для нього недосяжним ».
«Мій противник звинуватив мене і мого вчителя в тому , що ми нібито дали не вірне рішення його завдань. Але як може бути невірним корінь рівняння , якщо підставляючи його в рівняння і виконуючи всі визначені в цьому рівнянні дії , ми приходимо до тотожності ? І вже якщо сеньйор Тарталья хоче бути послідовним , то він повинен був відповісти на зауваження, чому ми вкрали за його словами , його винахід і використовували його для вирішення запропонованих завдань , отримали невірне рішення . Ми - мій учитель і я - так не вважаємо , однак винахід синьйора Тартальи є малозначимим . Це винахід чудовий. Більше того , я спираючись значною мірою на нього , знайшов спосіб рішення рівняння 4 -го ступеня і в « Ars magna » мій вчитель говорить про це. Що ж хоче від нас сеньйор Тарталья ? Чого він домагається цим диспутом ?»
« Панове, панове , - закричав Тарталья , - я прошу вас вислухати мене ! Я не заперечую того , що мій молодий противник дуже сильний в логіці і красномовстві . Але цим не можна замінити справжнє математичний доказ. Завдання, які я дав Кардано і Феррарі , вирішені не правильно , але і я доведу це . Дійсно , візьмемо , наприклад , рівняння з числа, які були розв'язані . Воно , як відомо ...»
У церкві піднявся неймовірний шум , що поглинув повністю закінчення фрази , розпочатої крикливим математиком . Йому не дали продовжувати. Натовп , вимагала від нього , щоб він замовк і щоб черга була надана Феррарі . Тарталья , бачачи , що продовження суперечки абсолютно марно , поспішно опустився з кафедри і вийшов через північний вихід на площу. Натовп бурхливо вітав « переможця » диспуту Луїджі Феррарі .Так закінчився цей спір , який і зараз продовжує викликати все нові і нові суперечки . Кому насправді належить спосіб вирішення рівняння 3-го ступеня ? Ми говоримо зараз - Нікколо Тарталье . Він відкрив , а Кардано виманив у нього це відкриття . І якщо зараз ми називаємо формулу , що представляє корені рівняння 3-го ступеня через його коефіцієнти , формулою Кардано , то це - історична несправедливість. Як підрахувати міру участі у відкритті кожного з математиків ? Може , з часом хтось і зможе відповісти на це питання абсолютно точно , а може це залишиться таємницею ...
Математики постійно зіштовхувалися із задачами, що приводили їх до розв'язування рівнянь 3, 4 і 5-го степенів. Найчастіше 3-го.
Протягом багатьох сотень років учені безуспішно шукали способи рішення рівнянь 3-го степеня.
Розв'язування одного виду кубічного рівняння було відкрито талановитим узбецьким ученим з міста Самарканда Джемшидом аль-Каші (помер близько 1456 p.).
Геометричний метод розв'язування одного виду чисельного кубічного рівняння був відомий ще Архімеду. Алгебричний же метод рішення кубічного рівняння протягом багатьох століть залишався невідомим.
Перший крок у цьому напрямку зробив на початку XVI ст. італійський учений Сціпіон дель Ферро. Він знайшов розв'язок рівняння х3 + ax = b при а > 0 і b> 0.
Своє розв'язання він по секрету повідомив Фіорі. Той скористався цим секретом і викликав на математичний двобій талановитого вченого Нікколо Тарталью (1500-1557), розраховуючи «вбити» його своїм умінням розв'язувати кубічні рівняння.
Тарталья довідався, що Фіоре знає таємницю розв'язання кубічного рівняння і за тиждень до двобою самостійно знайшов розв'язок рівняння більш загального вигляду х3 + рх = q для будь-яких р і q. 12 лютого 1535 року, у день двобою, Тарталья розв'язав усі ЗО задач Фіоре і переміг його.
Учень Кардано, Феррарі (XVI ст.), знайшов формулу коренів Рівняння 4-го степеня. Таким чином, до кінця XVI ст. математики вміли виражати корені рівнянь 1, 2, 3 і 4-го степенів через їхні коефіцієнти за допомогою шести дій (додавання, віднімання, множення, ділення, піднесення до степеня і добування кореня).
 Нікколо́ Тарта́лья
Нікколо́ Тарта́лья
Нікколо́ Тарта́лья (італ. Niccolò Tartaglia), справжнє ім'я Нікколо Фонтана (італ. Niccolò Fontana) ( близько 1499, Брешія — 13 грудня 1557, Венеція) — італійський математик.
Народився Нікколо в дуже бідній сім'ї. Під час однієї з Італійських воєн (1494—1559 рр.), що вели між собою Франція та Іспанія за право володіти Італією, його рідну Брешію захопили французи. Хлопчик отримав поранення. Йому розсікли язик, понівечили гортань. Нікколо тоді було шість років. Після цього він розмовляв з великими труднощами і тому його називали «Тарталья» (італ. tartaglia — заїка).
Батько Нікколо помер дуже рано. Тому його сім'я дуже бідувала. У школі Нікколо провчився всього 15 днів. Не маючи змоги платити за навчання мати була вимушена забрати сина зі школи. Хлопцеві довелося самому опановувати науку. Тим не менш він здав іспити на звання «магістра абака» (щось на зразок учителя арифметики) і почав працювати в приватному комерційному ліцеї. Поселившись у Вероні, заробляв свій хліб викладанням математики. Він читав лекції з геометрії, арифметики і механіки. Окрім цього, консультував з різних питань математики і техніки майстрів, купців, артилеристів і архітекторів.
Наприкінці 1534 р. Тарталья одержав виклик на математичний турнір від Антоніо Фіоре — учня відомого професора математики Болонського університету Сципіона дель Ферро. Нікколо дізнався, що Фіоре володіє секретом розв'язання кубічного рівняння, який йому повідомив Ферро. Шляхом титанічних зусиль Тартальї за кілька днів до диспуту теж вдалося знайти спосіб розв'язання такого рівняння.
Двобій відбувся 12 лютого 1535 р. Кожному із супротивників треба було розв'язати по 30 задач. За дві години Тарталья справився з усіма задачами, запропонованими йому Фіоре, а той не розв'язав жодної задачі свого противника (Фіоре запропонував переважно кубічні рівняння, а Тарталья — задачі з різних розділів математики). Перемога була повною, вчений прославився на всю Італію і отримав кафедру математики у Вероні.
Своїм методом розв'язування кубічного рівняння Тарталья поділився з відомим ученим Джироламо Кардано, що був одночасно математиком і механіком, лікарем і алхіміком, хіромантом і особистим астрологом римського папи, узявши з того слово ніколи не публікувати повідомлений йому метод розв'язання. Але через шість років Кардано порушив свою клятву — він видав трактат «Велике мистецтво, або про правила алгебри» (1545 р.), де виклав алгоритми розв'язування рівнянь третього і четвертого степеня. Щоправда, Кардано чесно написав у передмові, що: «...у наш час Сципіон дель Ферро відкрив формулу... Нікколо Тарталья з Брешії, наш друг, що був викликаний на змагання з учнем дель Ферро по імені Антоніо Маріо Фіоре, розв’язав, щоб не бути переможеним, ту ж саму проблему і після довгих прохань передав секрет мені.»
Але все одно Тарталья дуже образився, і написав Кардано гнівного листа. За честь Кардано заступився його учень Лодовіко Феррарі (якому належить першість у розв'язанні в радикалах рівняння четвертого степеня). Він викликав Тарталью на публічний диспут з «геометрії, арифметики та по'язаними з ними дисциплінами, такими як астрологія, музика, космографія, перспектива, архітектура та ін.»
Двобій відбувся 10 серпня 1548 р. у Мілані. Ворожнечо налаштована публіка змусила Тарталью припинити диспут і терміново залишити Мілан. Переможцями стали вважати (не зовсім об'єктивно) Феррарі та його вчителя Кардано. І навіть формулу для коренів кубічного рівняння стали називати формулою Кардано. Сучасні історики науки вважають, що більш справедливо її називати формулою Ферро-Тартальї-Кардано.
Тарталья написав декілька книг, найважливіша з яких була видана у Венеції під назвою «Загальний трактат про число і міру» (ч.1-6, 1556—1560). У ній він виклав свої оригінальні дослідження з арифметики, алгебри і геометрії. Зокрема, у книзі вперше застосовуються круглі дужки. Трактат містить також таблицю так званих «біноміальних коефіцієнтів». Ця таблиця була частково відома в Індії ще в 2 ст. до н. е. Більшу популярність ця таблиця отримала в 17 ст. у зв'язку з працями Б. Паскаля, тому іноді її називають «трикутником Паскаля».
Тарталья досліджував також проблеми механіки, балістики, геодезії. У праці «Нова наука» (1537) він вперше розглянув питання про траєкторію польоту снаряда і встановив, що найбільша дальність польоту досягається при нахилу ствола гармати під кутом 45 градусів. Його книга «Різні питання і винаходи» (1546) присвячена фортифікації. Учений здійснив переклад італійською мовою деяких праць Архімеда та Евкліда.
Іменем Фонтана названо кратер на видимій стороні Місяця.
Джирола́мо Карда́но (24 вересня 1501, Павія — 21 вересня 1576, Рим) — італійський фізик, математик, філософ, винахідник карданного механізму, автор формули для розв'язку кубічних рівнянь (1545).
Народився в Павії 24 вересня 1501 року. Син Фаціо Кардано, відомого адвоката, згадуваного Леонардо да Вінчі. 1526 року Джероламо закінчив Падуанський університет. Повернувся до Мілана, читав лекції з математики. Практикував у провінції, 1539 року прийнятий до Колегії лікарів.
У вільний час Кардано складав гороскопи живих і мертвих (його послугами як астролога користувався сам Папа Римський), тлумачив сни. Книга Кардано «Про тонкі матерії» (De subtilitate rerum) служила популярним підручником зі статики і гідростатики протягом всього XVII століття. Відомі міркування Кардано про створення вічного двигуна, про відмінність між електричним і магнітним тяжінням. Учений здійснював експериментальні дослідження і конструював різні механізми (зокрема, вал, який тепер називається карданним). Кардано був пристрасним любителем азартних ігор. «Побічним продуктом» його любові до гри в кістки стала книга «Про азартні ігри» (De Ludo alea, 1563), що містить основи теорії ймовірності, формулювання закону великих чисел, деякі питання комбінаторики. Праця Кардано «Велике мистецтво» (Ars magna, 1545) став наріжним каменем сучасної алгебри. У ній зроблено першу спробу внести систему до вивчення рівнянь, здійснено деякі операції з уявними числами. У цій же роботі було вперше опубліковано способи розв'язку рівнянь третього і четвертого ступенів (розв'язок рівняння четвертого ступеня було знайдено учнем Кардано — Лодовіко Феррарі). Це було чи найпершою публікацією математичного методу, невідомого раніше ні грекам, ні арабам. Публікація Ars magna викликала знамениту тяжбу Кардано щодо пріоритету в розв'язку цієї задачі з Нікколо Тарталья, лектором з Венеції. Спосіб розв'зку кубічних рівнянь було знайдено Сципіоном дель Ферро з Болоньї ще 1515 року. 1535 року Тарталья незалежно від нього винайшов свій метод і повідомив про нього Кардано, узявши з останнього клятву зберегти відкриття в таємниці. Проте Кардано опублікував у своїй книзі все, що було йому відомо про кубічні рівняння, заявивши, що знав про зміст роботи Ферро і це звільняє його від усіх зобов'язань стосовно Тартальї. 1546 року Тарталья звинуватив Кардано у віроломстві. Тяжба скінчилася після публічного диспуту 1548 року, на якому інтереси Кардано захищав Феррарі.
1562 року Кардано було призначено професором до Болоньї, де 1570 року його заарештувала інквізиція за публікацію гороскопу Ісуса Христа. Останок життя Кардано мешкав у Римі, намагаючись здобути прощення.
На схилі життя він писав у автобіографії: «Мета, до якої я прагнув, полягала в увічненні мого імені, оскільки я міг цього досягти, а зовсім не в багатстві або неробстві, не в почестях, не на високих посадах, не у владі»
Помер Кардано в Римі 21 вересня 1576.
За легендою, Кардано передбачив день своєї смерті і, щоб довести правоту у той день скінчив життя самогубством. Він залишив записку: «Хоч і неправда, але чудово придумано!»
Незважаючи на численність творів Кардано, у науці найбільш відома формула його імені, яку відкрив не він.
 Франсуа Вієт
Франсуа Вієт
«... Мистецтво, яке я викладаю , ново або принаймні було настільки зіпсовано часом і спотворено впливом варварів , що я вважав за потрібне надати йому абсолютно новий вид ... » Ф. Вієт
Франсуа́ Віє́т — французький математик, що запровадив сучасну систему нотації в алгебрі.
Народився 1540 року на півдні Франції у невеликому містечку Фонтене-ле-Конт провінції Пуату-Шарант, що розташоване за 60 км від Ла-Рошель, що була на той час оплотом французьких протестантів-гугенотів (послідовників кальвінізму). Більшу частину життя він прожив поряд із керівниками цього руху, хоча сам залишався католиком. Релігійні незгоди вченого не турбували.
Батько Франсуа був прокурором. За традицією, син обрав професію батька й став юристом, закінчивши університет у Пуату. 1560 року двадцятирічний адвокат почав свою кар'єру в рідному місті. Як адвокат Вієт користувався у населення авторитетом та повагою. Але через три роки перейшов на службу до відомої гугенотської сім'ї де Партене. Він став секретарем власника будинку й учителем його дочки, дванадцятирічної Катерини. Саме її навчання викликало в молодого юриста зацікавленість до математики.
Коли учениця виросла та вийшла заміж, Вієт не розлучився з її родиною й перебрався з нею до Парижу, де йому було легше дізнатися про досягнення провідних математиків Європи. З деякими вченими Вієт познайомився особисто. Він спілкувався з відомим професором Сорбонни Рамусом, вів дружнє листування з відомим математиком Італії Рафаелем Бомпеллі.
1571 року Вієт перейшов на державну службу й став радником парламенту в Бретані. Знайомство з Генріхом Наварським, майбутнім королем Франції Генріхом IV, допомогло Вієту отримати почесну придворну посаду — таємного радника — спочатку короля Генріху ІІІ, а потім — і Генріха IV.
Франсуа Вієт здобув славу під час франко-іспанської війни. Іспанські інквізитори вигадали дуже важкий шифр, який складався приблизно з 600 знаків і весь час змінювався й доповнювався. Завдяки цьому шифру войовнича та сильна на той час Іспанія могла вільно листуватися з ворогами французького короля навіть у самій Франції, і це листування залишалося нерозгаданим. Після марних спроб знайти ключ до шифру король звернувся до Вієта. Розповідають, що Вієт працював протягом двох тижнів підряд, вдень і вночі, і все ж таки знайшов ключ до шифру[Джерело?]. Після цього несподівано для іспанців Франція стала вигравати одну битву за іншою. Пізніше іспанцям стало відомо, що шифр для французів уже не таємниця, і що його розшифрував Вієт. Впевнені в неможливості розгадати спосіб тайнопису людьми, вони звинуватили Францію перед папою римським та інквізицією в підступах диявола, а Вієта було звинувачено у союзі з дияволом та присуджено до спалення на вогнищі. На щастя для науки, його не було видано інквізиції.
Перебуваючи на державній службі, Вієт залишався вченим. До того часу належать свідоцтва сучасників Вієта про його величезну працездатність. Захоплюючись чим-небудь, він міг працювати по три доби без сну.
1584 року через наполягання Гізів Вієта звільнили з посади та послали до Парижу. Саме на цей період припадає розквіт його діяльності. Отримавши несподіваний спокій та відпочинок, вчений поставив собі мету скласти всеосяжну математику, яка дозволила б розв'язувати будь-які задачі. У нього склалося переконання, «що має існувати загальна, невідома ще наука, яка охоплює й розумні роздуми найновіших алгебраїстів, і глибокі геометричні досліди давніх».
Головною пристрастю Вієта була математика. Він глибоко вивчив твори класиків: Архімеда й Діофанта; найближчих попередників Кардано, Бомпеллі, Стевіна та інших. Вієта вони не лише захоплювали, у них він бачив велику ваду, яка полягала в складності розуміння через словесну символіку. Майже всі дії й знаки записувалися словами, не було навіть натяку на ті зручні, майже автоматичні правила, якими ми зараз користуємось. Не можна було записувати, і, отже, вивчати в загальному вигляді алгебраїчні рівняння або якісь алгебраїчні вирази. Кожен вид рівняння з числовими коефіцієнтами розв'язувався за особливим правилом. Так, у Кардано розглядалося 66 видів алгебраїчних рівнянь. Тому необхідно було довести, що існують такі загальні дії над усіма числами, які від самих чисел не залежать. Вієт та його послідовники встановили, що не має значення, чи буде розглянуте число кількістю предметів або довжиною відрізка. Головне, що над цими числами можна виконувати алгебраїчні дії й у результаті знову отримати такі ж числа. Отже, їх можна позначати якимись абстрактними знаками. Вієт це й зробив. Він не лише запровадив символьне обчислення, але й зробив принципово нове відкриття, поставивши перед собою мету вивчати не лише числа, а й дії над ними. Щоправда, у самого Вієта алгебраїчні символи були ще мало схожі на наші. Зі знаків дій він використовував «+» і «-», знак радикалу й горизонтальну риску для ділення. Добуток позначав словом «in». Вієт першим став застосовувати дужки, які в нього мали вигляд риски над многочленом. Але багато знаків, які були введені до нього, він не використовував (квадрат, куб тощо), а позначав словами або першими літерами слів. Основу свого підходу Вієт називав видовою логістикою. Наслідуючи приклад античних учених, він чітко розмежував числа, величини та відношення, зібравши їх у деяку систему «видів». До цієї системи входили, наприклад, змінні, їх корені, квадрати, куби і т. д. Для цих видів Вієт дав особливу символіку, позначивши їх маленькими літерами латинської абетки. Для невідомих величин застосовувалися голосні літери, для змінних — приголосні. Вієт довів, що, оперуючи з символами, можна отримати результат, який буде придатним до будь-яких величин, тобто, можна розв'язати задачу в загальному вигляді. Це поклало початок докорінним змінам у розвитку алгебри: стало можливим символьне обчислення. Не випадково, що за це Вієта називають «батьком» алгебри, основоположником літерної символіки.
Особливо пишався Вієт відомою теоремою про залежність між коренями квадратного рівняння та його коефіцієнтами, яку він отримав самостійно, хоча, як нині відомо, залежність між коефіцієнтами й коренями рівняння (навіть загальнішого вигляду, ніж квадратне) була відома ще Кардано, а в такому вигляді, як ми застосовуємо її для квадратного рівняння, — давнім вавилонянинам. Теорему було оприлюднено 1591 року. Її названо ім'ям Вієта, а сам автор формулював її так: «Якщо B+D, помножене на А, мінус А в квадраті дорівнює BD, то А дорівнює В і дорівнює D». Теорема Вієта стала зараз одним з найвідоміших тверджень шкільної алгебри. Теорема Вієта варта уваги тим, що її можна узагальнити для многочленів будь-якого степеня.
Великих успіхів досяг учений у геометрії. У трактаті «Доповнення до геометрії» він намагався створити за античними прикладами якусь геометричну алгебру, використовуючи геометричні методи для розв'язання рівнянь третього й четвертого степеня. Будь-яке рівняння третього або четвертого степеня, стверджував Вієт, можна розв'язати геометричним методом трисекції кута або побудовою двох середніх пропорційних.
Математиків протягом століть цікавило питання розв'язання трикутників, оскільки воно диктувалося потребами астрономії, архітектури та геодезії. У Вієта методи, які застосовувалися раніше, набули завершеного вигляду. Він першим чітко сформулював теорему косинусів, хоча положення, еквівалентні їй, епізодично застосовувалися з першого століття нашої ери. Відомий раніше своєю складністю випадок побудови трикутника за двома сторонами й одним з протилежних їм кутів отримав у Вієта вичерпний розгляд. Було чітко доведено, що розв'язок не завжди можливий. Якщо ж він існує, то може бути один або два.
Глибоке знання алгебри давало Вієту великі переваги. Інтерес до алгебри спочатку було викликано застосуванням у тригонометрії та астрономії. Не лише кожне нове використання алгебри давало імпульс новим дослідженням з тригонометрії, але й отримані тригонометричні результати стали джерелом важливих успіхів алгебри. Вієту належить виведення формули для синусів (або хорд) і косинусів кратних дуг.
1589 року, після вбивства Генріха Гіза за наказом короля, Вієт повернувся до Парижу. Але у тому ж році Генріха III було вбито монахом — прихильником Гізів. Формально французька корона перейшла до Генріха Наваррського — голови гугенотів. Але лише після того, як 1593 року той прийняв католицьку віру, у Парижі його визнали королем Генріхом IV. Так було покладено кінець релігійній війні, яка довгий час впливала на життя кожного француза, що не цікавився ані політикою, ані релігією.
Подробиці життя Вієта у той час невідомі. Відомо лише, що він перейшов на службу до Генріха IV, перебував при дворі, був відповідальним урядовцем і користувався великою повагою як математик. За легендою, посол Нідерландів сказав на прийомі у короля Франції Генріха IV, що їхній математик Адріан ван-Роумен задав математикам світу задачу. Але у Франції, мабуть, немає математиків, оскільки серед тих, кому особисто адресувався виклик, немає жодного француза. Генріх IV відповів, що у Франції є математик, і запросив Вієта. У приймальні короля, у присутності короля, міністрів та гостей, Вієт знайшов один корінь запропонованого рівняння 45-го степеня. Король був дуже задоволений. Наступного дня Вієт знайшов ще 22 корені рівняння. Цим він і обмежився, оскільки інші 22 корені були від'ємними, а Вієт не визнавав ні від'ємних, ні уявних коренів.
В останні роки життя Вієт пішов з державної служби, але продовжував цікавитися наукою. Відомо, що він вступив у полеміку з приводу запровадження нового григоріанського календаря і навіть хотів створити власний календар. У мемуарах деяких придворних Франції є вказівки, що Вієт був одружений, що в нього була дочка, єдина спадкоємниця на ймення синьйора де ла Біготьє (прізвище, за яким Вієт звався). У придворних новинах маркіз Летуаль писав: «…14 лютого 1603 р. пан Вієт, рекетмейстр, людина великого розуму і розсудливості, один з найбільш вчених математиків століття, помер… у Парижі, маючи, за загальною думкою, 20 тис. екю. Йому було більше шістдесяти років».
Методи розв’язування кубічних рівнянь
Кубі́чне рівня́ння — алгебраїчне рівняння виду
![]() , де
, де ![]() .
.
Для того, щоб отримати загальний розв'язок кубічного рівняння, потрібно його звести до канонічного вигляду
![]()
Це можна зробити шляхом ділення рівняння на старший коефіцієнт ![]() після чого провівши заміну змінної
після чого провівши заміну змінної ![]()
При цьому коефіцієнти будуть рівні:
![]()
![]()
Введемо дві змінні ![]() та
та ![]() , такі що
, такі що
![]()
підставивши їх в рівняння отримаємо
![]()
введемо додаткову умову для змінних, а саме:
![]()
підставивши її в рівняння, та використавши ![]() отримаємо та розв'яжемо квадратне рівняння відносно
отримаємо та розв'яжемо квадратне рівняння відносно ![]() наступним чином:
наступним чином:
![]()
Всього є три розв'язки рівняння ![]() один з них є
один з них є
![]()
Якщо ![]() та:
та:
-
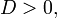 то рівняння має один дійсний корінь і два комплексні.
то рівняння має один дійсний корінь і два комплексні.
-
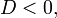 то всі три корені рівняння є різними дійсними числами.
то всі три корені рівняння є різними дійсними числами.
-
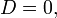 то всі корені рівняння є дійсними числами, при чому принаймні два з них є однаковими.
то всі корені рівняння є дійсними числами, при чому принаймні два з них є однаковими.
Фо́рмула Карда́но — це формула для аналітичного розв'язку канонічного кубічного рівняння виду ![]() . Вона має вигляд:
. Вона має вигляд:
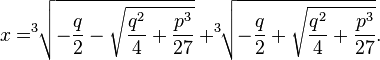
Названа на честь Джироламо Кардано, хто перший опублікував її.
Виведення формули Кардано
Нехай дано рівняння ![]()
Будемо шукати його розв'язок у вигляді ![]()
Отримаємо рівняння
![]()
Введемо додаткову умову для змінних ![]()
утворену систему 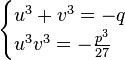 розв'яжемо за допомогою формули Вієта для квадратного рівняння і отримаємо:
розв'яжемо за допомогою формули Вієта для квадратного рівняння і отримаємо:
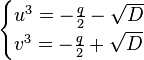 , де
, де ![]() — дискримінант кубічного рівняння, звідки
— дискримінант кубічного рівняння, звідки
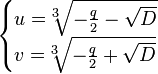
Розв'язок рівняння подається у вигляді ![]() . В комплексних числах кубічний корінь має 3 різних значення. Для отримання розв'язків потрібно вибирати такі пари значень кубічного кореня, щоб
. В комплексних числах кубічний корінь має 3 різних значення. Для отримання розв'язків потрібно вибирати такі пари значень кубічного кореня, щоб ![]() . Таких пар обов'язково знайдеться рівно 3.
. Таких пар обов'язково знайдеться рівно 3.
Тригонометрична формула Вієта
Тригонометрична формула Вієта — один із способів розвязувати кубічні рівняння ![]()
Формула
-
Обчислемо
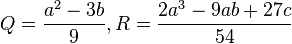
-
Обчислемо
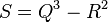
-
Якщо
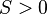 , то обчислемо
, то обчислемо 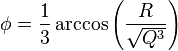 і матемемо три дійсних корені:
і матемемо три дійсних корені:
![]()
![]()
![]()
-
Якщо
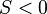 , то замінюємо тигонометричні функції гіперболічними. Тут можливі наступні випадки в залежності від значення
, то замінюємо тигонометричні функції гіперболічними. Тут можливі наступні випадки в залежності від значення 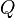 :
:
-
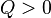 :
:
-
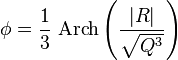
![]() (дійсний корінь)
(дійсний корінь)
![]() (пара комплексних коренів)
(пара комплексних коренів)
-
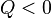 :
:
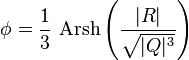
![]() ( дійсний корінь)
( дійсний корінь)
![]() ( пара комплексних коренів)
( пара комплексних коренів)
-
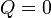 :
:
![x_{1}=-{\sqrt[ {3}]{c-{\frac {a^{3}}{27}}}}-{\frac {a}{3}}](/uploads/files/14318/89259/95072_html/images/var-www-user-data-www-naurok-com-ua-web-uploads-files-14318-.058.png) ( дійсний корінь)
( дійсний корінь)
![]() ( пара комплексних коренів)
( пара комплексних коренів)
-
Якщо
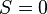 , то рівняння вироджене і має менше ніж 3 різних розв'язків (другий корінь буде кратний 2):
, то рівняння вироджене і має менше ніж 3 різних розв'язків (другий корінь буде кратний 2):
![]()
![]()
-
Вихідний многочлен має вигляд
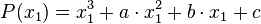 .
.
-
Підстановка
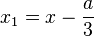 зводимо многочлен до виду
зводимо многочлен до виду 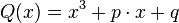 , где
, где 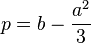 и
и 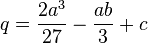 .
.
-
Шукаємо розв'язки рівняння
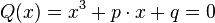 у вигляді
у вигляді 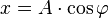 , отримаємо рівняння
, отримаємо рівняння 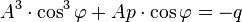 .
.
-
Засвідчемо що у випадку
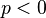 при
при 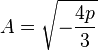 це рівняння набуває вигляду
це рівняння набуває вигляду 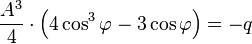 .
.
-
Використаємо тригонометричну тотожність
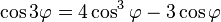 зводимо до рівняння виду
зводимо до рівняння виду 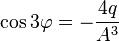 .
.
-
Розв'язок цого рівняння має вигляд
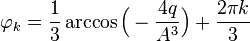 , де
, де 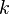 набуває значення 1, 2, 3.
набуває значення 1, 2, 3.
-
Підставляємо отримане значення
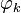 в вираз для змінної
в вираз для змінної 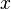 , отримаємо відповівдь
, отримаємо відповівдь 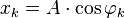
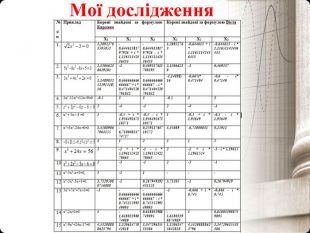
Мої Дослідження
Приклад № 1
х3 + 4х2 + х - 6 = 0
Знаходимо дільники вільного члена ± 1; ± 2; ± 3; ± 6.
Ліву частину рівняння позначимо f (x). Очевидно, що f (1) = 0, x1 = 1. Ділимо f (x) на х - 1.
Отже,
х3 + 4х2 + х - 6 = (х - 1) (х 2 + 5х + 6)
Останній множник позначимо через Q (x). Вирішуємо рівняння Q (x) = 0.
х 2,3 = -2;-3
Відповідь: 1; -2; -3.
Приклад № 2
Розв'яжемо рівняння ![]() з очевидними коренями -1, 0, +1:
з очевидними коренями -1, 0, +1:
![]()
Приклад № 3 , рівняння ![]() має єдиний корінь (дійсний) —
має єдиний корінь (дійсний) — ![]() . Формула Кардано даєт для цього єдиного дійсного корня вираз
. Формула Кардано даєт для цього єдиного дійсного корня вираз
![]() .
.
Отже,
![]() .
.
Але фактично довільне доведення запропоновує використання того, що цей вираз є коренем рівняння ![]() . Якщо не вгадати
. Якщо не вгадати
Приклад № 4
Розв'яжемо рівняння х3+3х2-3х-11=0
(х+1)3-6х-12=0, t=x+1
t3-+6(t-1)-12=0
t3-6t-6=0 , t=u+v
(u+v)3 -6(u+v) -6=0
u3+v3+3uv(u+v)-6(u+v)-6=0
u3+v3+(u+v)(3uv-6)-6=0
3uv-6=0, якщо ![]() v=
v=![]() , u3+
, u3+ ![]() =6 , u6-6u3+8=0, u3=4 або u3=2. Якщо u3=4, то
=6 , u6-6u3+8=0, u3=4 або u3=2. Якщо u3=4, то![]() =2, якщо u3=2, то
=2, якщо u3=2, то![]() =4.
=4.
t=u+v не зміниться, якщо поміняти доданки, то 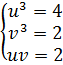 ,
, ![]()
u=![]() , v=
, v=![]() , то t=
, то t=![]() .
.
Відповідь: x=![]() .
.
Приклад 5 : Розв'яжемо рівняння х3+6х2+9х+1=0.
Якщо доповнити два перших доданка х3+6х2 до формули куба суми
х3+6х2+12х+8= (х+2)3, то рівняння набуде вигляду: (х+2)3-3х-7=0.
Зробимо заміну: t=x+2, отримаємо
t3-3(t-2)-7=0
t3-3t-1=0.
Подамо змінну t у вигляді t=u+v.
(u+v)3-3(u+v)-1=0
u3+v3+3uv(u+v)-3(u+v)-1=0
u3+v3+(u+v)(3uv-3) -1=0.
Підберемо значення змінних u і v так, щоб 3uv-3=0, тобто uv=1.
Для знаходження u і v розв’яжемо систему.
![]() u=
u=![]() підставимо у перше рівняння
підставимо у перше рівняння
![]() -
-![]() +1=0,
+1=0, ![]() =y, y2-y+1=0, Д=1-4<0.
=y, y2-y+1=0, Д=1-4<0.
На множині дійсних чисел рівняння коренів не має.
Приклад 2 : z3+6z+2=0
Нехай z=u+v, тоді (u+v)3+6(u+v)+2=0
u3+v3+3uv(u+v)+6(u+v)+2=0
u3+v3 +3(u+v)(uv+2)+2=0
uv+2, якщо ![]() , u=-
, u=- ![]() .
.
(- ![]() 3+ v3=-2, -
3+ v3=-2, - ![]() + v3=-2,
+ v3=-2,
v6+2v3-8=0, v3=t,
t2+2t-8=0 , t1=-4 та t2=2.
Значить, v3=-4, v1=- ![]() ; v3=2, v2=
; v3=2, v2=![]() .
.
Якщо v1=- ![]() , то u1=
, то u1=![]() ; v2=
; v2=![]() то u2=-
то u2=- ![]() . Оскільки, z=u+v , то
. Оскільки, z=u+v , то
z=![]() -
- ![]() =
=![]() (1-
(1-![]() ).
).
Приклад №6 : Розв'яжемо рівняння х3-6х2+11х-6=0
(х-2)3-х+2=0, нехай t=x-2, тоді
t3- (t+2) +2=0,
t3-t =0, t(t2-1)=0, t1 =0, t2=1, t3=-1.
Якщо t1 =0, t2=1, t3=-1, то х1=2, х2=3, х3=1.
Приклад 4 : z3-3z2-6z+8=0,
(z-1)3-9z+9=0,
Нехай t=z-1, тоді t3-9(t+1) +9=0,
t3-9t-9+9=0,
t3-9t=0,
t(t-3)(t+3)=0 , t1=0, t2=0, t3=0.
Якщо t1=0, t2=0, t3=0, то z1=1, z2=4, z3=-2.
Приклад № 7: Розв'яжемо рівняння х3-11х2+38х-40=0
В цьому рівнянні виділяти куб різниці незручно, тому серед дільників вільного члена знайдемо цілі корені рівняння. При х=2 рівняння перетворюється у вірну рівність. Отже, за наслідком із теореми Безу многочлен х3-11х2+38х-40 поділиться на х-2. Виконаємо ділення.
х3-11х2+38х-40![]()
х3-2х2
-9х2+38х
-9х2+18х
20х-40
20х-40
Отже, рівняння має вигляд: (![]()
х1=2, ![]() За теоремою Вієта х2=4, х3=5.
За теоремою Вієта х2=4, х3=5.
Приклад № 8. Розв’язати кубічне рівняння
![]()
![]()
Рівняння виду набирає вигляду
![]()
і має розв’язок
![]()
Рівняння має дійсний корінь
![]()
Приклад № 9. Розв’язати рівняння
![]() .
.
Знаходимо значення
![]()
Рівняння виду (2) набирає вигляду
![]()
і має розв’язок ![]() який визначається з рівнянь
який визначається з рівнянь
![]()
При ![]() знаходимо дійсний корінь
знаходимо дійсний корінь ![]()
Для полегшення розрахунків мною були створені дві програми на мові Paskal в оболонці Delphi для полегшення розрахунків знаходження коренів кубічних рівнянь, які представлені в Додатку №1 і .Додатку №2
|
№ з/п |
Приклад |
Корені знайдені за формулою Кардано |
Корені знайдені за формулою Вієта |
||||
|
Х1 |
Х2 |
Х3 |
Х1 |
Х2 |
Х3 |
||
|
|
|
1,28922763595852 |
-0,64461381797926 + i * 1,11651142436433 |
-0,64461381797926 - i * 1,11651142436433 |
1,28922763 |
-0,644613 + i * 1,11651142436433 |
-0,644613 - i * 1,11651142436433 |
|
|
|
2,13066238629181 |
-1 |
0,469337613708193 |
2,13066238 |
-1 |
0,469337 |
|
|
|
-1,14898325229151E-16 |
-0,666666666666667 + i * 0,471404520791032 |
-0,666666666666667 - i * 0,471404520791032 |
-1,1489E-16 |
-0,66+i* 0,471404 |
-0,6 - i* 0,47140 |
|
|
2х3-11х2+12х+9=0 |
-0.5 |
3 |
3 |
-0.5 |
3 |
3 |
|
|
|
2 |
-4 |
-1 |
2 |
-4 |
-1 |
|
|
х3 + 3х – 4 =0 |
1 |
-0,5 + i * 1,93649167310371 |
-0,5 - i * 1,93649167310371 |
1 |
-0,5 + i * 1,93649 |
-0,5 - i * 1,93649 |
|
|
х3+3х2-24х+6=0 |
3,45089067064155 |
-6,71000831774727 |
0,25911764710572 |
3,45089 |
-6,71000831 |
0,25911 |
|
|
|
3 |
1 |
2 |
3 |
1 |
2 |
|
|
|
2 |
-1 + i * 5,19615242270663 |
-1 - i * 5,19615242270663 |
2 |
-1 + i * 5,1961524 |
-1 - i * 5,19615 |
|
|
|
2 |
-3 |
-1 |
2 |
-3 |
-1 |
|
|
х3-3х2-х+3=0, |
3 |
-1 |
1 |
- |
- |
- |
|
|
х3-3х2-3х+1=0, |
3,73205080756888 |
-1 |
0,267949192431123 |
3,73205 |
-1 |
0,26794919 |
|
|
3х3+7х2+7х+3=0 |
-1 |
-0,666666666666667 + i * 0,74535599249993 |
-0,666666666666667 - i * 0,74535599249993 |
-1 |
-0,666 + i * 0,745 |
-0,666 - i * 0,745 |
|
|
х3-2х+1=0 |
1 |
-1,61803398874989 |
0,618033988749895 |
-1,61803398874989 |
1 |
0,618033988749895 |
|
|
х3-9х2+24х-17=0 |
4,53208888623796 |
1,12061475842818 |
3,34729635533386 |
1,12061475842818 |
4,53208888623796 |
3,34729635533386 |
Висновок
В результаті вище викладеного матеріалу я пришла до висновку, що вивчати кубічні рівняння та методи їх розв’язку необхідно, так як це спричиняє розвиток мислення, розвиває логіку. А методи Кардано і Вієта мною були обрані не дарма, бо вони найкраще підкреслюють всю красу математики та її логіку. При дослідженні мною було зроблено наступний висновок, що з 15 мною обраних рівнянь для тестування найкращий метод для розв’язку кубічних рівнянь метод Кардано, а метод Вієта складніший тим, що в ньому присутні тригонометричні функції.
Використані джерела
- Бурбаки Н. Очерки по истории математики. – М.: Мир, 1963.
- Вилейтнер Г. История математики от Декарта до середины XIX столетия. – М.: Наука, 1966.
- Гариг Г.Г. Спор Тарталья и Кардано о кубических уравнениях и его общественные основы. – М.: Архив истории науки и техники, 1935.
- Гордиенко Н.А Развитие алгебры в Европе в XV–XIX столетиях. Учебное пособие для студентов дневного отделения физико-математического факультета / – Воронежский госпедуниверситет, 2007.
- История математики с древнейших времен до начала XIX столетия / Под ред. А.Н.Колмогорова и А.П.Юшкевича. Т.1. – М.: Наука, 1970.
- Кольман Э. История математики в древности. – М.: Наука, 1961.
- Никифоровский В.А. Из истории алгебры XVI – XVII веков. – М.: Наука, 1979.
- Пачоли Лука. Трактат о счетах и записях. – М.: Финансы и статистика, 1983.
- Попов П.С. Исторические задачи. М.: Наука, 1968.
- Пресман А.А. Решение квадратного уравнения с помощью циркуля и линейки. - М., Квант, № 4/72. С. 34.
- РодионовЕ.М. Справочник по математике для поступающих в вузы: Решение задач с параметрами. – М.: МЦ «Аспект», 1992.
- Рыбников К.А. История математики. – М.: Изд-во МГУ, 1960.
- Табачников С.Л. Многочлены: Методические разработки для учащихся ОЛ «ВЗМШ» Российской академии образования при МГУ. – М.: Фазис, 1996.
- Чистяков В.Д. Рассказы о математиках. – Минск: Выш. шк., 1963.
- Чистяков В.Д. Старинные задачи по элементарной математике. – Минск: Выш. шк., 1978.
- http://ru.wikipedia.org/wiki/%D4%EE%F0%EC%F3%EB%E0_%CA%E0%F0%E4%E0%ED%EE
- http://znaimo.com.ua/Формула_Кардано
- http://ru.wikipedia.org/wiki/%D2%F0%E8%E3%EE%ED%EE%EC%E5%F2%F0%E8%F7%E5%F1%EA%E0%FF_%F4%EE%F0%EC%F3%EB%E0_%C2%E8%E5%F2%E0
- http://matemonline.com/2013/04/two-mathematicians-one-destiny-cardano-and-tartaglia/
- http://pidruchniki.ws/16850303/prirodoznavstvo/kinematichna_statika
- http://www.cleverstudents.ru/equations/cubic_equations.html
Додаток № 1
Програма для обчислення коренів кубічного рівняння по методу Кардано
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls;
type
TForm1 = class(TForm)
Button1: TButton;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Label6: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit4: TEdit;
Edit5: TEdit;
Edit6: TEdit;
Edit7: TEdit;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
Label11: TLabel;
Label13: TLabel;
Label14: TLabel;
Edit8: TEdit;
Edit9: TEdit;
Edit10: TEdit;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
var
Form1: TForm1;
implementation
{$R *.dfm}
procedure TForm1.Button1Click(Sender: TObject);
var
A,B,C,D: real; {коэффициенты кубического уравнения A*x^3+B*x^2+C*x+D=0}
p, q: real; {коэффициенты кубического уравнения y^3+p*y+q=0, x=y-B/(3*A)}
S: real; {Дискриминант кубического уравнения S=q*q/4+p*p*p/27}
F: real; {аргумент комплексного корня}
Re: real; {дейстаительная часть комплексно-сопряжённых корней}
Im: real; {мнимая часть комплексно-сопряжённых корней}
y1: real; {y1=(-q/2+Sqrt(q*q/4+p*p*p/27))^(1/3)}
y2: real; {y1=(-q/2-Sqrt(q*q/4+p*p*p/27))^(1/3)}
x1,x2,x3: real;{точные корни уравнения A*x^3+B*x^2+C*x+D=0 }
begin
A:=StrToFloat(Form1.Edit1.Text);
B:=StrToFloat(Form1.Edit2.Text);
C:=StrToFloat(Form1.Edit3.Text);
D:=StrToFloat(Form1.Edit4.Text);
p := (3*A*C-B*B)/(3*A*A);
q := (2*B*B*B-9*A*B*C+27*A*A*D)/(27*A*A*A);
S := (4*(3*A*C-B*B)*(3*A*C-B*B)*(3*A*C-B*B)
+(2*B*B*B-9*A*B*C+27*A*A*D)*(2*B*B*B-9*A*B*C+27*A*A*D))
/(2916*A*A*A*A*A*A);
Form1.Edit5.Text := FloatToStr(p);
Form1.Edit6.Text := FloatToStr(q);
Form1.Edit7.Text := floatToStr(S);
y1:=0; y2:=0; F:=0;
if S<0
then
begin
if q<0 then F:=Arctan(-2*Sqrt(-S)/q);
if q>0 then F:=Arctan(-2*Sqrt(-S)/q)+Pi;
if q=0 then F:=Pi/2;
x1:=2*Sqrt(-p/3)*Cos(F/3)-B/A/3;
x2:=2*Sqrt(-p/3)*Cos((F+2*Pi)/3)-B/A/3;
x3:=2*Sqrt(-p/3)*Cos((F+4*Pi)/3)-B/A/3;
if q=0 then x3:=-B/A/3;
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2);
Form1.Edit10.Text:= FloatToStr(x3);
end;
if S>0
then
begin
if -q/2+Sqrt(S)>0 then y1:=exp(ln(abs(-q/2+Sqrt(S)))/3);
if -q/2+Sqrt(S)<0 then y1:=-exp(ln(abs(-q/2+Sqrt(S)))/3);
if -q/2+Sqrt(S)=0 then y1:=0;
if -q/2-Sqrt(S)>0 then y2:=exp(ln(abs(-q/2-Sqrt(S)))/3);
if -q/2-Sqrt(S)<0 then y2:=-exp(ln(abs(-q/2-Sqrt(S)))/3);
if -q/2-Sqrt(S)=0 then y2:=0;
x1:=y1+y2-B/A/3;
Re:=-(y1+y2)/2-B/A/3;
Im:=(y1-y2)*Sqrt(3)/2;
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(Re)+' + i * '+FloatToStr(Im);
Form1.Edit10.Text:= FloatToStr(Re)+' - i * '+FloatToStr(Im);
end;
if S=0
then
begin
if q<0 then y1:=exp(ln(abs(-q/2))/3);
if q>0 then y1:=-exp(ln(abs(-q/2))/3);
if q=0 then y1:=0;
x1:=2*y1-B/A/3;
x2:=-y1-B/A/3;
x3:=-y1-B/A/3;
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2);
Form1.Edit10.Text:= FloatToStr(x3);
end;
end;
end.
Додаток № 2
Програма для обчислення коренів кубічного рівняння методом Вієта
unit Unit1;
interface
uses
Windows, Messages, SysUtils, Variants, Classes, Graphics, Controls, Forms,
Dialogs, StdCtrls, Math;
type
TForm1 = class(TForm)
Button1: TButton;
Label1: TLabel;
Label2: TLabel;
Label3: TLabel;
Label4: TLabel;
Label5: TLabel;
Edit1: TEdit;
Edit2: TEdit;
Edit3: TEdit;
Edit5: TEdit;
Edit7: TEdit;
Label7: TLabel;
Label8: TLabel;
Label9: TLabel;
Label10: TLabel;
Label11: TLabel;
Label13: TLabel;
Label14: TLabel;
Edit8: TEdit;
Edit9: TEdit;
Edit10: TEdit;
Edit6: TEdit;
procedure Button1Click(Sender: TObject);
private
{ Private declarations }
public
{ Public declarations }
end;
const e=2.718281828459045;
var
Form1: TForm1;
l: text;
k: array [1..4] of real;
a, b, c, Di, Fi: real;
x: array [1..3] of real;
d: integer; Q, R, S: real;
K1,K2,K3,K4: real; //{коэффициенты кубического уравнения A*x^3+B*x^2+C*x+D=0}
implementation
{$R *.dfm}
function Cube(f: real): real;
begin
cube := f * f * f;
end;
function Cosh(f: real): real;
begin
cosh:=(power(e, f)+power(e,-f))/2;
end;
function Sinh(f: real): real;
begin
sinh:=(power(e, f)-power(e,-f))/2;
end;
function Sign(f: real): real;
begin
if f<>0 then sign := f/(abs(f))else sign:=0;
end;
function Cubrt(f: real): real;
begin
cubrt := Power(Abs(f),1/3)* sign(f);
end;
function Arccos(f: real): real;
begin
arccos := arctan(sqrt(1-f*f)/f);
end;
function Arsh(f: real): real;
begin
arsh := ln(f +abs(f)+1);
end;
function Arch(f: real): real;
begin
Arch := ln(f +abs(f)-1);
end;
procedure TForm1.Button1Click(Sender: TObject);
var x1,x2,x3: real;
begin
K1:=StrToFloat(Form1.Edit1.Text);
K2:=StrToFloat(Form1.Edit2.Text);
K3:=StrToFloat(Form1.Edit3.Text);
a := K1;
b := K2;
c := K3;
Q :=(Sqr(a)-3* b)/9;
R :=(2* Cube(a)-9* a * b +27* c)/54;
S := Cube(Q)- Sqr(R); //дискримінант
Form1.Edit5.Text := FloatToStr(S);
Form1.Edit6.Text := FloatToStr(Q);
Form1.Edit7.Text := FloatToStr(R);
if S >0 then
begin
Fi := Arccos(R /(Sqrt(Cube(Q))))/3;
x1:=-2* Sqrt(Q)*cos(Fi)- a /3;
x2:=-2* Sqrt(Q)*cos(Fi +(2/3)* Pi)- a /3;
x3:=-2* Sqrt(Q)*cos(Fi -(2/3)* Pi)- a /3;
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2);
Form1.Edit10.Text := FloatToStr(x3);
end;
if S =0 then
begin
x1:=-2* Cubrt(R)- a /3;
x2:= Cubrt(R)- a /3;
x3:= x[2];
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2);
Form1.Edit10.Text := FloatToStr(x3);
end;
if S <0 then
begin
if Q >0 then
begin
Fi := Arch(Abs(R)/(Sqrt(Cube(Q))))/3;
x1:=-2* sign(R)* Sqrt(Q)*cosh(Fi)- a /3;
x2:=sign(R)*sqrt(Q)*cosh(Fi)-a/3;
x3:=sqrt(3*Q)*sinh(Fi);
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2)+'+'+FloatToStr(x3)+'*i';
Form1.Edit10.Text := FloatToStr(x2)+'-'+FloatToStr(x3)+'*i';
end;
if Q <0 then
begin
Fi := Arsh(Abs(R)/(Sqrt(Cube(Abs(Q)))))/3;
x1:=-2* sign(R)* Sqrt(Abs(Q))*sinh(Fi)- a /3;
x2:=sign(R)*sqrt(Abs(Q))*sinh(Fi)-a/3;
x3:=sqrt(3*abs(Q))*cosh(Fi);
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2)+'+'+FloatToStr(x3)+'*i';
Form1.Edit10.Text := FloatToStr(x2)+'-'+FloatToStr(x3)+'*i';
end;
if Q =0 then
begin
x1:=-Cubrt(c - Cube(a)/27)- a /3;
x2:=(-a-x1)/2;
x3:=(sqrt(abs((a-3*x1)*(a+x1)-4*b)))/2;
Form1.Edit8.Text := FloatToStr(x1);
Form1.Edit9.Text := FloatToStr(x2)+'+'+FloatToStr(x3)+'*i';
Form1.Edit10.Text := FloatToStr(x2)+'-'+FloatToStr(x3)+'*i';
end;
end;
end;
end.


про публікацію авторської розробки
Додати розробку