Самоанализ опыта работы.
Самоанализ опыта работы.
«Только учитель, который рискует выйти за пределы
своей профессии, может по-настоящему влиять на
учеников».
У московского писателя Н. Булгакова есть замечательный рассказ про первоклассника, который на вопрос учительницы: кем ты хочешь стать? – отвечает: Пушкиным! Может быть, задача школьного учителя – педагога и заключается в том, чтобы, помимо грамоты, алгебры, геометрии, истории,…, научить детей разбираться в окружающих и в себе, тянуться к лучшему.
Ученику обычно кажется, что количество материала для изучения (или повторения) так велико, что справиться невозможно. Как же нам, учителям, правильно построить работу?
Ученики, которые в прямом смысле выкладываются на учебу, но, парадокс: чем больше такие ученики стараются, чем длиннее готовят уроки, тем хуже результаты. И порой мы делаем большую ошибку, полагая, что в основе плохой учебы лежит малое усердие. А на самом деле все гораздо сложнее: у многих детей слабая нервная система, низкая работоспособность, повышенная утомляемость. И главная помощь для таких детей – организация щадящего режима, снижение учебной нагрузки. В основном работа любого учителя строится на «трех китах» :
- сегодня - повторение того, что было вчера; а завтра – повторение того, что было вчера и сегодня и т.д.
- обучение на легком и доступном для ученика языке и непременно с хорошим
настроением («учиться надо весело, чтоб хорошо учиться»)
3.закрепление. Что касается моей системы работы, то она, естественно, с годами изменилась «коренным образом»: экономия времени за счет меньшей «писанины», больше работы по готовым чертежам и уже записанным на доске условиям, необязательное доказательство того, что уже было доказано на прошлом уроке всем классом, обязательные устные и логические упражнения, обязательная самостоятельная работа обучающего характера, обязательное «проговаривание» некоторых упражнений ( правильно «разговорить» ученика, как известно, на математическом языке трудно, он должен к нему привыкнуть с годами), обязательные полуустные задачи, плюс ко всему обязательный хороший настрой учащихся, ну и учитывание того контингента учащихся, у которых повышенный интерес к математике.
А теперь о работе со слабыми классами. Во-первых, я их люблю больше, а во-вторых, и работать с ними мне нравится больше. Зная низкую и неустойчивую работоспособность таких учеников , учитывая их повышенную утомляемость и быстро и резко снижающиеся показатели, с такими детьми больше импровизируешь, давая волю фантазии, находишься с ними в постоянном «цейтноте» ( в хорошем смысле ), и получаешь в конце огромное удовольствие от их отдачи. В работе с такими детьми я усвоила для себя самое главное – не надо искать
( ждать) от них конкретного результата, ибо его может и не быть, а понять, что главное – сам процесс. Пусть он будет интересен, доступен, прост в изложении, пусть дети чувствуют, что работают «наравне» . Они не виноваты, что у них замедленный темп деятельности, узкий диапазон материала, трудность в распределении и переключении внимания, неспособность к длительному умственному напряжению. Таких детей нужно постоянно
( но небеспочвенно ) похваливать, поддерживать их энтузиазм. Они наивны, доверчивы, преданны, обидчивы, ранимы.
Если бы у меня была возможность выбора, я бы выбрала работу именно со слабыми детьми, т.е. с детьми с ослабленными способностями.
Основные направления работы
1)Коррекционно-развивающая деятельность в процессе обучения
1. Физическое состояние и развитие ребенка (утомляемость, истощаемость, рассеянность, пресыщаемость, количество ошибок к концу урока или при однообразных видах деятельности).
2. Особенности и уровень познавательных процессов: особенности восприятия пространства и времени; особенности внимания, памяти, мышления, речи; познавательные интересы, любознательность.
3. Отношение к учебной деятельности, особенности мотивации, уровень освоения учебной деятельности.
4. Особенности эмоционально-личностной сферы: эмоционально-волевая зрелость, способность к волевому усилию, преобладающее настроение; особенности самооценки, отношения со сверстниками и взрослыми; поведение в школе и дома, нарушения поведения, вредные привычки.
5. Особенности усвоения знаний, умений и навыков, предусмотренных программой: общая осведомленность об окружающем мире и о себе, сформированность навыков счета; характер ошибок при счете и решении задач.
Основная ценность образования - человек, ребенок. Образование и воспитание должны помочь ему стать человеком, стать самим собой. Еще Л.Н.Толстой писал, что воспитание как умышленное формирование людей по известным образцам «не плодотворно, не законно и не возможно».
Психологические основы организации и осуществления коррекционно-развивающего обучения
Обучение в компенсирующих классах строится с опорой на действующие учебники. Однако планирование учебного содержания имеет свои особенности. Специфика обнаруживается в структурировании материала, методике его преподавания. Построение содержания учебного материала в системе коррекционно-развивающего обучения осуществляется на основе следующих принципов:
• усиления практической направленности изучаемого материала;
• выделения сущностных признаков изучаемых явлений;
• опоры на жизненный опыт ребенка;
• ориентации на внутренние связи в содержании изучаемого материала как в рамках одного предмета, так и между предметами;
• необходимости и достаточности в определении объема изучаемого материла;
• введения в содержание учебных программ коррекционных разделов, предусматривающих активизацию познавательной деятельности, формирования у учащихся деятельностных функций, необходимых для решения учебных задач
2)Индивидуальные качества подростка.
Нестандартные задания помогают выявлять индивидуальные качества подростка.
1)Креативные качества: а)воображение; б)интуиция; в)инициативность; г)придумывание.
2)Когнитивные качества: а)логическое познание; б)эмоционально-образное познание; в)смысловое видение; г)умение задавать вопросы; д)прогнозирование.
3)Оргдеятельностные качества: а)целеполагание; б)планирование; в) работоспособность; г)рефлексия; д)самооценка; е)техника ведения дискуссий; ж)навыки работы в группе.
Задания когнитивного типа:
- Вычислите стоимость школьных принадлежностей в вашемпортфеле (5 класс).
- Почему все уравнения первой степени являются линейными (7 класс).
- Предложите другие способы доказательства того, что сумма углов треугольника равна 180 градусам (7 класс).
- Что есть общего и отличного в числах 284 и 220 (6 класс, тема «Дружественные числа»),
- Ролевая игра «Появление отрицательных чисел» (6 класс, тема «Положительные и отрицательные числа»).
- Исследуйте слово «функция». Биологическая категория «функция». Математическое понятие «функция». Сравните их и сделай те выводы (7 класс, тема «Числовая функция»).
- Предложите свое доказательство теоремы о сумме углов треугольника (7 класс.Геометрия).
- Проведите исследование «Ход конем». Точка передвигается по координатной плоскости по принципу хода шахматной фигуры «конь» (например, 3 единичных отрезка вправо и 2 единичных отрезка влево или 3 единичных отрезка вниз и 2 единичных отрезка вправо).
- Опишите, записывая координаты точек, один из маршрутов коня из начальной точки в точку
(-1; 1).
- Каким может быть минимальное число ходов в предыдущем задании?
- Может ли точка из начального положения перейти по данному принципу и попасть в точку (9;2)? Опишите возможный маршрут.
-
Может ли точка из начального положения перейти по данному принципу и попасть в точку(
 ; 2).
; 2).
- Существует ли на координатной плоскости точка, в которую нельзя попасть из начального положения по данному принципу (6класс, тема «Координатная плоскость»)?
Задания креативного типа:
- Вы живете в первобытном обществе. Что, по вашему мнению, и в то время было известно в области математики (6 класс)?
- Нарисуйте образ десятичной дроби.
- Придумайте задачу по теме «Задачи на движение», которая решалась бы несколькими способами (один из способов — на составление уравнения) (5 класс).
- Сочините сказку «Приключения положительных и отрицательных чисел» (6 класс, тема «Отрицательные и положительные числа»).
- Разработайте свой алгоритм построения графика функции y=кх(7 класс).
- Составьте свой словарь «Математика в понятиях».
- Как можно записать 1000 (6 класс)?
- Разработайте алгоритм решения любой задачи (7 класс).
- В конце года напишите сочинение по теме «Мое отношение к предмету математика, анализ моей работы за год, что хорошего и что плохого».
- Подумайте, как могли появиться дробные числа. Результаты своих умозаключений оформите в виде рассказа, сказки, комиксов и т. д. (5 класс).
-
Составьте по краткой записи задачу:
- - 800 г, .
- - 0,75 от І.
Всего — ?
- Составьте сборник задач по теме «Проценты», в который включите не менее трех типов задач. На каждый тип приведите задачи трех уровней сложности (5 класс).
- Придумайте и нарисуйте схему (рисунок), которая позволит легко запомнить (вспомнить) правила сложения и вычитания положительных и отрицательных чисел (6 класс).
- В одной лаборатории был проведен следующий эксперимент. Цыплятам, которым было всего 10 мин от роду, показывали фигурки разной формы, похожие на корм, и смотрели, будут ли цыплята клевать. Оказалось, что цыплята клевали шарики в 10 раз чаще, чем звездочки. А кубики в 5 раз чаще, чем звездочки. Представьте результаты эксперимента одним из известных тебе способов фиксации.
- Составьте свой алгоритм нахождения произведения разности двух алгебраических выражений на их сумму.
- Составьте рекламу. Вид рекламы:
- Знакомство с ситуациями, в которых выгодно пользоватьсятождествами.
- Получая формулу куба суммы, выделяют существенные признаки куба суммы.
Придумать к каждой рекламной рубрике свои задания.
- Среди предложенных задач выделите те, которые кажутся пап более сходными, и обоснуйте свой выбор. Решите выделенные задачи, объясните способ решения. Придумайте и решите свою похожую задачу.
- Составьте программу по проведению праздника «Приглашаем принять участие в аукционе тождеств сокращенного умножении» Разработайте:
- словарь аукциона,
- условия аукциона,
- алгебраический банк,
- итоги торгов.
Задания оргдеятелъностного типа:
- Напишите рецензию на сказку соседа по парте по теме «Приключения положительных и отрицательных чисел» (6 класс).
- Разработайте план ответа по теме «Координатная плоскость» на основе материала учебника «Алгебра — 7»
- Домашнее задание: напишите отчет «Моя работа на последнем уроке», в котором сформулируйте цели своей работы, этапы трудностей и рекомендации для себя.
Каждый шаг, как творческий поиск…(нестандартные методы объяснения материала).
Тема: «Выражения со степенями» (7 класс)
Как упростить:
![]()
Используя специальную знаковую символику на уроках математики, формируем в учениках умение мыслить абстрактно и учит главному – самостоятельно переходить к разным видам выражения знаний.
Если учащиеся легко выполняют задания вида: ![]() , то
, то
задания учебника : «упростить ![]() » для них не сложные.
» для них не сложные.
Тема: «Многочлены» (7 класс)
![]()
![]()
![]()
5а
Объяснение с помощью символов, облегчает изучение материала.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
( + )( + )= ( + )+ ( + )=
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
= + + +
Тема: «Формулы сокращенного умножения» (7 класс)
![]()
![]()
![]()
![]()
![]()
![]() ( 2a + b )( 2a - b )= 2a 2- b 2 ит.д.
( 2a + b )( 2a - b )= 2a 2- b 2 ит.д.
Вовремя изучения формул сокращенного умножения (x+y)2= …учащиеся часто не могут понять, что вместо х и у могут быть записаны целые выражения, ((а+2b)+4ab)2и поэтому формулы можно подать в виде символов.
Тема: «Упражнения на все действия с дробями» (6 класс)
![]()
![]()
![]()
![]()
![]()
![]() Чтобы заинтересовать учащимся предлагается установить взаимосвязь музыки и математики. Каждая нота в музыке имеет определенное дробное значение. Таким образом, с начало изучив ноты, можно предложить детям нотные примеры.
Чтобы заинтересовать учащимся предлагается установить взаимосвязь музыки и математики. Каждая нота в музыке имеет определенное дробное значение. Таким образом, с начало изучив ноты, можно предложить детям нотные примеры.
![]()
![]()
![]()
![]()
![]()
![]()
![]() - 1 -
- 1 - ![]() -
-![]() -
- ![]() -
- ![]() . - 1∙1,5
. - 1∙1,5
пример
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]() ( .+) : + =
( .+) : + = ![]()
Тема: «Рациональные числа» ( 6 класс)
Возьмем два игровых кубика – черного и белого цвета, на гранях которых точками обозначено число от 1 до 6. При работе на уроке знак «+» означает выигрыш, а знак «-» -проигрыш. Белый кубик будет показывать «выигрышное» число очков, а черный «проигрышное» число.


![]()
![]()
![]() Пусть награни белого кубика два очка, а на грани черного – три. Белый кубик показывает выигрыш в два очка, черный – проигрыш в три очка. Количество очков будем записывать с соответствующим знаком: +2 и -3.
Пусть награни белого кубика два очка, а на грани черного – три. Белый кубик показывает выигрыш в два очка, черный – проигрыш в три очка. Количество очков будем записывать с соответствующим знаком: +2 и -3.
![]()
![]()


![]()

![]()
![]()

![]() Примеры:
Примеры:
![]()
![]()
![]()
![]()
![]()
![]()
![]()


![]()
![]()
![]() а) б) в)
а) б) в)
![]()
![]()
![]()
![]()
(+1)+(+5)=+6 (-3)+(-4)= -7 (+2)+(-3)= -1

![]()
![]()
![]()
![]()
![]()
![]()

![]()
![]()
![]()

![]()
![]()

![]()
![]() г) д)
г) д)
![]()
(+7)-(+1)=+6; (+7)-(+6)=+1 (-4)-(+3)= -7
Тема: «Числовые и буквенные выражения» (5 класс)
![]()
![]()
![]()
![]() В жизни мы часто встречаем графические символы
В жизни мы часто встречаем графические символы
Это условное обозначение Земли, знаки дорожного движения, знаки мужчина и женщина, курить запрещено и т.д.
В математике символы служат для обозначения предметов и чисел.
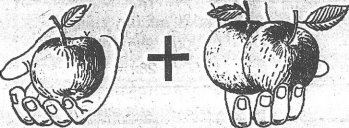
В левой руке одно яблоко, в другой – два. Всего три яблока. Если яблоко назовем буквой «я», тогда сумма запишется следующим образом:
я+2я=2я
Мы обозначили яблоко буквой «я» просто потому, что это первая буква в слове. А могли бы выбрать любой символ, какой нам больше нравится.
Упражнение: Сложите символы.
Например:а+ 2а + 4а = 7а.
12Ь - 6 Ь = 12а + 10а + а=
4р + 20р+р = 15х+ 5х +16х=
 Здесь 2 яблока и 3 банана. Если вы хотите найти сумму, то получите
Здесь 2 яблока и 3 банана. Если вы хотите найти сумму, то получите
5 яблобанов – это что-то новенькое!
Обозначим а – яблоко, b – банан , получим 2а+3b ≠ 5ab
Запомните: в математике складываются только одинаковые символы – «а» с «а», « b» с «b» и т.д.
Упражнение: Сложите одинаковые символы.
Например: 2а + За + Зb + b = 5а +4b
2а + 5а + 4Ь + 2Ь =а+2а+ ЗЬ=
5g + р + 2р + 6g = 10р + 4g + g + 2g=
Зх+2у + х+5у = 10а+2с + а + 3с =

про публікацію авторської розробки
Додати розробку
