Квадратична нерівність.

Квадратна нерівність.

1.

Які з наведених нерівностей є квадратичними?

а)x² – 2x³ +1 < 0

 б)5x² < 1

 в)x² + 2x + 4 ≥ 0

г)3x – 4 < 0

2.

Розв’яжіть нерівність: 4 – x2 > 0

а)x ϵ (–∞; –2)

 б) x ϵ (2; +∞)

 в)x ϵ (–∞; –2) U (2; +∞)

 г)x ϵ (–2; 2)

3.

Розв’яжіть нерівність : –3x² + 27 ≤ 0 .

а) x ϵ (3; +∞)

 б) x ϵ (–∞; –3)

 в) x ϵ (–∞; –3] U [3; +∞)

 г)x ϵ [–3; 3]

4.

Які з чисел є розв’язками нерівності : x² – 5x + 6 ≤ 0?

а)2,5

 б)3

 в)-2

 г)-3

5.

Розв’яжіть нерівність : x² – 64 > 0

а)x ϵ (–∞; -8) U (8; +∞)

 б)x ϵ (8; +∞)

 в)x ϵ (–∞; 8)

 г)x ϵ (–8; 8)

6.

Розв’яжіть нерівність : x² – 2x – 15 < 0

а)x ϵ (–∞; –3) U (5; +∞)

 б) x ϵ (–3; 5)

 в)x ϵ (–5; 3)

 г)x ϵ (–∞; –5) U (3; +∞)

 

 

 

 

 

7.

 

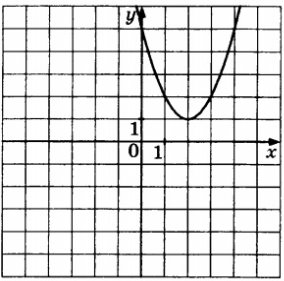
Використовуючи графік функції,розв`яжить нерівність :

х²-4х+5≥0 .

а)(1;1)

 б)(2;1)

 в)(-∞; +∞)

 г)∅

 

8.

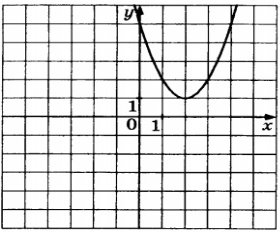
Використовуючи графік функції,розв`яжить нерівність :

х²-4х+5≤0

а)(2;1)

 б)(-∞; +∞)

 в)∅

 г)(1;2)

 

 

 

 

 

9.

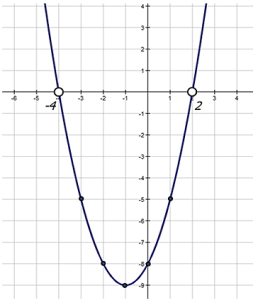
Використовуючи графік функції,розв`яжить нерівність :

х²+2х-8<0 .

а)(-4;2)

 б)(-9;2)

 в)(-∞;-4)υ(2;+∞)

 г)∅

10.

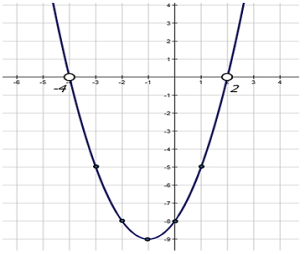
Використовуючи графік функції,розв`яжить нерівність :

х²+2х-8>0 .

а)(-4;2)

 б)(-∞;-4)υ(2;+∞)

 в)(-∞;-4]υ[2;+∞)

 г)∅

 

 

Ключ до тесту

1. б в (2 балів)

2. г (1 балів)

3. в (1 балів)

4. а б (2 балів)

5. а (1 балів)

6. б (1 балів)

7. в (1 балів)

8. в (1 балів)

9. а (1 балів)

10. б (1 балів)