Стандартний вигляд числа
Тема 3. Степінь з натуральним показником
Урок № 27
Тема. Множення одночленів. Піднесення одночленів до степеня
Мета: домогтися свідомого розуміння алгоритмів перетворення добутку та степеня одночлена в одночлен стандартного вигляду; продовжити формування навичок виконання дій зі степенями.
Тип уроку: засвоєння знань; формування навичок.
Хід уроку
I. Перевірка домашнього завдання
Бліцконтроль
- Який з виразів є одночленом: 1) 3 + х2; 2) 3х2; 3) 3 : х2; 4) (х – 3)2?
- Який із записів є одночленом стандартного вигляду:
1) х2 ∙ у ∙ 3у2; 2) 3х2 ∙ у ∙ 2; 3) 6х2у; 4) 6 – х2у?
- Назвіть коефіцієнт та степінь одночлена: 3х2у3z (у вказаному порядку):
1) 3; 2; 2) 3; 5; 3) 3; 3; 4) 3; 6.
Під час корекції виконаної роботи дуже важливо спонукати учнів до обґрунтування свого вибору.
II. Актуалізація опорних знань
- Спростіть вираз: хх3 х0 х5; р18 : р3; (т ∙ т3)6.
- Відшукайте значення виразу при х = -2:
5х2; -5х2; 5(-х)2; 2х2; -2х3; 2(-х)3.
- За яких значень у є правильною нерівність: у2 ≤ 0, у2 > 0?
III. Робота з випереджальним домашнім завданням
На дошці записані приклади (з підручника або аналогічні) на множення одночленів та піднесення одночлена до степеня.
- -3а2b ∙ 4аb3 = (-3 ∙ 4) ∙ (а2 ∙ а) ∙(b ∙ b3)= -12а3b4.
- (-5а2b)3 = (-5)3 ∙ (а2)3 ∙ b3 = -125а6b3.
Учням пропонуємо прокоментувати кожний крок у проведених перетвореннях, а саме: які поняття, їх властивості було використано (бажано ці властивості й поняття візуалізувати, тобто під час коментарів робити записи на дошці).
IV. Засвоєння знань
Після проведеної роботи із домашнім завданням буде доречним зробити висновки — сформулювати алгоритми перетворення добутку одночленів і степеня одночлена у вигляді одночлена стандартного вигляду (можна запропонувати виконати цю роботу учням).
Єдине, про що можна поговорити або винести на наступний урок,— Це випадки, коли треба перетворити вираз, що містить і множення одночленів, і піднесення одночлена до степеня (нагадати учням про послідовність виконання дій різного ступеня).
V. Застосування знань. Формування і вдосконалення вмінь
Оскільки на вивчення питання, внесеного в тему уроку, відводиться два уроки, перший урок ми присвячуємо закріпленню знань змісту алгоритмів множення одночленів та піднесення одночлена до степеня та вдосконаленню набутих умінь виконувати прямі та обернені перетворення (тобто добуток одночленів у одночлен та подання одночлена у вигляді добутку двох або кількох множників; перетворення степеня одночлена в одночлен стандартного вигляду та подання одночлена у вигляді степеня).
Виконання усних вправ
- Перемножте одночлени: 1) 2а і 3b; 2) 4с2 і 2с; 3) 5a2b і ab; 4) - ху2 і 2х.
- Піднесіть до степеня одночлен: 1) (2а)2; 2) (2аb)3; 3) (-2а2)3; 4)(-а2b)3.
Виконання письмових вправ
- Виконайте множення одночленів:
1) 4х ∙ 7у; 2) -8х ∙ 5х3; 3) ![]() аb3 ∙
аb3 ∙ ![]() аb; 4) 0,2т3п9 ∙ 2,5т4п;
аb; 4) 0,2т3п9 ∙ 2,5т4п;
5) 0,75а9b3с2 ∙ 1![]() а4bс7; 6)
а4bс7; 6) ![]() т4с9 ∙(-10та) ∙ 2,5с3а6;
т4с9 ∙(-10та) ∙ 2,5с3а6;
7*) 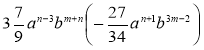 .
.
- Подайте одночлен – 12х4у3 двома способами у вигляді добутку:
1) двох одночленів стандартного вигляду;
2) трьох одночленів стандартного вигляду;
- чотирьох одночленів стандартного вигляду.
-
Піднесіть до степеня:
1) (3x2)3; 2) (4m)2; 3) (-3xу2)3; 4) (-0,2a7b3c)2;
5) 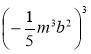 ; 6)
; 6) 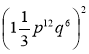 ; 7*)
; 7*) ![]() .
.
- Подайте одночлен у вигляді квадрата одночлена:
1) 16а2; 2)25а8; 3) 64а10b6; 4) 0,36т12п4; 5) 729х14у8z24.
- Подайте одночлен у вигляді куба одночлена:
1) 27а3; 2) 64а9; 3) -125а6b15; 4) 0,008х6у8; 5) -![]() а21b33с6.
а21b33с6.
VI. Підсумки уроку. Рефлексія
Чи правильно виконані перетворення виразів:
1) 2![]() a5b ∙
a5b ∙ ![]() a3b = 2
a3b = 2![]() (a5a3)(bb) = 2
(a5a3)(bb) = 2![]() a8 ∙ 2b;
a8 ∙ 2b;
2) (-2a2b)3 = (-2)3a3b3 = 8a3b3?
Знайдіть і виправте помилку.
VII. Домашнє завдання
№ 1. Виконайте множення одночленів:
l) 0,4a3b5 ∙ 1,5а3b; 2) 0,45т3п2р4 ∙ 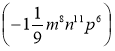 ;
;
3) ![]() а5с ∙ (15b3с2) ∙ 1,2а3b6; 4)
а5с ∙ (15b3с2) ∙ 1,2а3b6; 4) 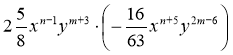 .
.
№ 2. Піднесіть до степеня:
1) (2х3у)3; 2) (-5а4b2с3)2; 3) 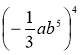 ; 4) (13x5у6z7)2;
; 4) (13x5у6z7)2;
5) 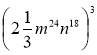 ; 6) (-а2п b3п-1 сп+2)10.
; 6) (-а2п b3п-1 сп+2)10.
№ 3. Випереджальне домашнє завдання. Порівняйте вираз
1) 5а6 ∙ (-3а2b)2 із виразами 2) 5а6 ∙ 9а4b2 та 3) (-3а2b)2
(за алгоритмом порівняння).
Які дії і в якому порядку треба виконати, щоб спростити вираз 1)?
1
БАБЕНКО С.П. Уроки алгебри. 7 клас Урок №27


про публікацію авторської розробки
Додати розробку
