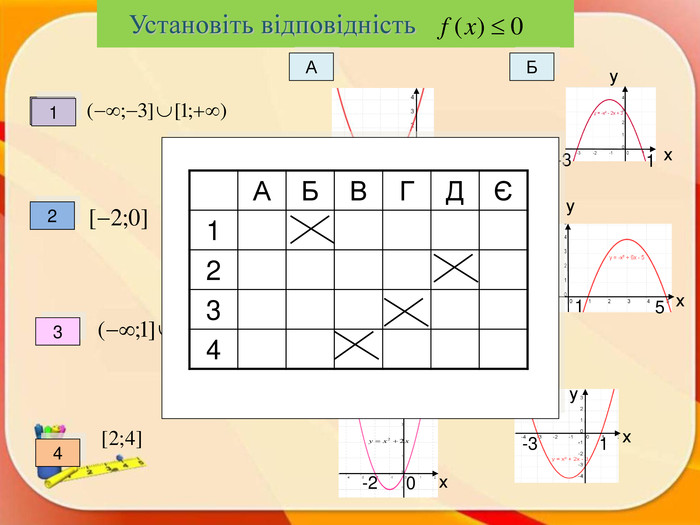
Квадратична функція. ЇЇ графік і властивості.

Функція у = aх2 + bx + c, а  0. ЇЇ графік і властивості. Епіграф уроку: Математика безмежно різноманітна і міститься в усьому. М. Яругін

Мета уроку: -узагальнити і систематизувати знання учнів з даної теми, вдосконалити навички побудови графіка квадратичної функції, вміння проводити елементарне дослідження функції; показати застосування квадратичної функції; - розвивати обчислювальні навички, графічну культуру, мислення, пам'ять, кмітливість, увагу, ініціативність, самостійність; - виховувати навички колективної роботи та співпраці, формувати пізнавальний інтерес.

1.Тест: «Вірно – невірно» Б. Функція виду y=kx+b називається лінійною. О Л К Е Р Й Д Б А Н І П Ц Б Ц. Графіком лінійної функції є пряма. Ц О. Пряма y=2x+3 обов’язково буде проходити через 2 и 4 координатні кути. Е. В записі функції y=3x-6 число -6 – це ордината точки перетину графіка з віссю y. Е П. Квадратична функція задається рівнянням y=

1.Тест: «Вірно – невірно» Л К Е Р Й Д Б А Н І Ц Б Ц Е Н. Графік функції y=ax2 називається параболою. Н Л. Абсциса вершини параболи y=ax2+bx+c знаходиться по формулі xв=- . Л А. Парабола y=(x-5)2+2 має вершину в точці з координатами (-2;5). К. Лінійні функції y=25x-48 і y=-14x+1 є зростаючими. Й. Точка А(0,2;0,6) належить графіку функції y=15x2. Й І. Графіком рівняння xy-1=0 є гіпербола. І Р. Графік функції у = ах2 при будь-якому а  0 називають гіпербола. Д. При а >0 вітки параболи у = ах2 напрямлені вниз.

Калькулятор Лейбніца «Люди, незнайомі з алгеброю, не можуть представити собі тих дивовижних речей, яких можна досягнути … за допомогою даної науки» Готфрид Вільгельм фон Лейбніц

«Негідно обдарованій людині, витрачати подібно рабу, час на обчислення, які, безумовно, можна було б довірити будь-якій особі, якщо при цьому застосувати машину.» Готфрід Лейбніц

Установіть відповідність 1 2 3 4 х 1 А Б В Г Д Є 2 4 3 х у у х у -3 1 у -3 -1 х 2 4 у х х у 1 5 -2 0 -3 1 А Б В Г Д Є 1 2 3 4

Природа формує свої закони мовою математики. Г. Галілей *

1. Знайдіть координати вершини параболи у = х2 - 4х + 4 Відповідь. (2;0). Знайдіть нулі квадратичної функції у = х2 + х – 2 Відповідь. (-2; 0), (1; 0). Не виконуючи побудову графіка, визначте, найбільшого чи найменшого значення набуває квадратична функція у = 2 - 5х - 3х2 Відповідь. Найбільшого.

Парабола в архітектурі *

Алгоритм побудови графіка функції у = ах2 + bх +с. 1. Визначити напрямок віток параболи (а>0,вітки вгору; а<0,вітки вниз) 2. Знайти координати вершини параболи (хв; ув). 3. Провести через вершину параболи пряму,паралельну осі у, - вісь симетрії 4. Визначити точки перетину графіка функції з віссю х, тобто знайти нулі функції ,для цього треба розв'язати рівняння ах2 + bх +с=0. 5. Визначити точку перетину графіка функції з віссю у, для цього треба у формулу у=ах2 + bх +с підставити х=0 6.Скласти таблицю значень функції з урахуванням осі симетрії параболи 7.Побудувати параболу

Побудуйте графік функції І варіант y = x2 – 8x + 7 ІІ варіант у = x2 – 4х + 3 *

Політ – це математика. В.П. Чкалов *

Розв'яжи Скласти рівняння траєкторії стрибка дельфіна, якщо він стрибнув на висоту 2 метра і довжина його стрибка 4 метра. *

В математиці є щось таке, що викликає людське захоплення. Ф. Хаусдорф Траєкторія стрибка дельфіна – теж парабола. *

Домашнє завдання:

Математика є прообраз краси миру. І. Каплер

*