Підсумкова контрольна робота з алгебри, 9 клас
Підсумкова контрольна робота з алгебри для 9 класу містить 2 варіанти завдань.
|
9 клас Алгебра Контрольна робота №6 (підсумкова) Варіант 1 №1. У ящику є 30 пронумерованих від 1 до 30 жетонів. Яка ймовірність того, що номер навмання взятого жетона буде кратним числу 7?
а)
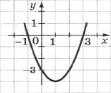
а) (-∞;-1) №3. Чому дорівнює четвертий член геометричної прогресії, якщо її перший член b1=6, а знаменник q = –2? а) –48; б) 48; в) 24; г) –24 №4. Розв’яжіть нерівність х2 – 49 > 0.
а) (-∞;7); б) (-∞;-7] №5. Знайдіть 30-ий член арифметичної прогресії , якщо а5 = 9, а7 = 13.
№6. Розв’яжіть систему рівнянь: №7. Побудуйте графік функції у = х2 + 6х + 8. Користуючись графіком, знайдіть: 1) найменше значення функції; 2) проміжок, на якому функція набуває додатних значень; 3) проміжок, на якому функція спадає. |
9 клас Алгебра Контрольна робота №6 (підсумкова) Варіант 2 №1. У ящику є 20 пронумерованих від 1 до 20 кубиків. Яка ймовірність того, що номер навмання взятого кубика буде кратним числу 7?
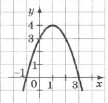
а) №2. На рисунку зображено графік функції у = –х2 + 2х + 3. Розв’яжіть нерівність –х2 + 2х + 3 > 0.
а) (-∞;-1)
в) (-∞;-1]
а) –14; б) 14; в) –7; г) 7
№4. Розв’яжіть нерівність х2 – 16
а) (-4;4); б) [-4;4]; в) (-∞;4] №5. Знайдіть 20-ий член арифметичної прогресії , якщо а6 = 6, а8 = 10.
№6. Розв’яжіть систему рівнянь: №7. Побудуйте графік функції у = х2 – 6х – 7. Користуючись графіком, знайдіть: 1) найменше значення функції; 2) проміжок, на якому функція набуває від’ємних значень; 3) проміжок, на якому функція зростає. |
|
9 клас Алгебра Контрольна робота №6 (підсумкова) Варіант 1 №1. У ящику є 30 пронумерованих від 1 до 30 жетонів. Яка ймовірність того, що номер навмання взятого жетона буде кратним числу 7?
а)
а) (-∞;-1) №3. Чому дорівнює четвертий член геометричної прогресії, якщо її перший член b1=6, а знаменник q = –2? а) –48; б) 48; в) 24; г) –24 №4. Розв’яжіть нерівність х2 – 49 > 0.
а) (-∞;7); б) (-∞;-7] №5. Знайдіть 30-ий член арифметичної прогресії , якщо а5 = 9, а7 = 13.
№6. Розв’яжіть систему рівнянь: №7. Побудуйте графік функції у = х2 + 6х + 8. Користуючись графіком, знайдіть: 1) найменше значення функції; 2) проміжок, на якому функція набуває додатних значень; 3) проміжок, на якому функція спадає. |
9 клас Алгебра Контрольна робота №6 (підсумкова) Варіант 2 №1. У ящику є 20 пронумерованих від 1 до 20 кубиків. Яка ймовірність того, що номер навмання взятого кубика буде кратним числу 7?
а) №2. На рисунку зображено графік функції у = –х2 + 2х + 3. Розв’яжіть нерівність –х2 + 2х + 3 > 0.
а) (-∞;-1)
в) (-∞;-1]
а) –14; б) 14; в) –7; г) 7
№4. Розв’яжіть нерівність х2 – 16
а) (-4;4); б) [-4;4]; в) (-∞;4] №5. Знайдіть 20-ий член арифметичної прогресії , якщо а6 = 6, а8 = 10.
№6. Розв’яжіть систему рівнянь: №7. Побудуйте графік функції у = х2 – 6х – 7. Користуючись графіком, знайдіть: 1) найменше значення функції; 2) проміжок, на якому функція набуває від’ємних значень; 3) проміжок, на якому функція зростає. |


про публікацію авторської розробки
Додати розробку