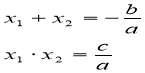Квадратне рівняння (Урок, Презентація, Тести)

 

 

Міністерство освіти і науки України

Відділ освіти Долинської РДА

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

                                            Вчитель

Тяпчанської ЗОШ

I-III ступенів

 Владика Р.Д.

 

 

 

 

 

 

 2009 рік

 

 

 

 

 

Освітня:

закріплення і узагальнення знань учнів, отримані при вивченні теми;

відпрацювання способів розв’язання квадратних рівнянь, вироблення уміння вибрати потрібний, раціональний спосіб розв’язання.

 

Розвивальна:

розвиток логічного мислення, пам'яті, уваги, умінь порівнювати і узагальнювати.

 

Виховна:

виховання працьовитості, взаємодопомоги, математичної культури.

 

Устаткування до уроку:

Персональні комп’ютери

Презентація « Квадратні рівняння»

лист 1 (таблиця відповідей, блок домашніх рівнянь);

 Презентація . Квадратні рівняння

лист 2 (довідкові таблиці, заповнені на попередніх уроках);

оцінний лист роботи на уроці (самооцінка);

лист релаксації уроку;

Тест декілька варіантів (у комп’ютері по рівню успішності)

 

Хід уроку

 

1. Організаційний момент .

Вчитель: Сьогодні ми підіб’ємо підсумки вивчення теми «Квадратні рівняння”

До нас завітало багато гостей. Я сподіваюся на успішну працю, що на уроці ви зможете показати свої знання, вміння, кмітливість. Тож будьте уважними, думайте, запитуйте, пропонуйте.

Урок проводимо у формі ділової гри, що має назву «Компетентність». Що це означає?

Компетенція  - це готовність застосувати знання, вміння та навички для фахового розв'язання проблеми. Вам дано ключ до розв’язання квадратних рівнянь, і якщо ви навчилися ним користуватися, ви зможете розв’язати будь-яке квадратне рівняння. А сьогодні ви покажете, наскільки готові користуватися цим ключем.

 

Епіграфом до уроку послужать слова В. Сойєра.

«Узагальнення – це, напевно, найлегший і найімовірніший шлях розширення математичних знань». Слайд 2.

Клас розподілено на три команди – зі своїми капітанами і групою «експертівю. У кінці уроку підбиваємо підсумки.

На листочках записують ім'я, прізвище. Результат вашої роботи на уроці – ваша самооцінка, виставлена в оцінному листі.

Використовується прийом розвитку критичного мислення “Написання СИНКВЕЙНА”

• Зараз на листочку поставте римську цифру 1 і відповімо на мої питання. Відповіді писатимемо під арабськими цифрами 1, 2, 3, 4, 5:

Запишіть один іменник, який є темою уроку.

1. Запишіть 2 прикметників, що розкривають тему.
2. Запишіть 3 дієслова, що описують тему.
3. Запишіть одну фразу в контексті сьогоднішньої теми.
4. Запишіть слово – резюме по даній темі.

Далі групи радяться і один представник групи представляє одну загальну відповідь команди “СИНКВЕЙН” всьому класу.

1-а зупинка: ДОМАШНЯ

Правильні 9 точок – «12».

Правильні 8 – 7 точок – «9».

Правильні 6 – 5 точок – «6».

 

Вчитель: Удома ви виконували самостійну роботу. Розв’язували по 9 рівнянь.

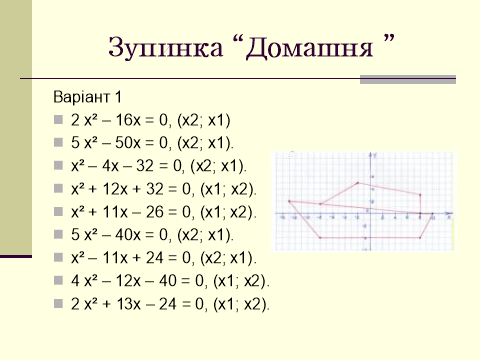
Завдання. За кодом коренів рівнянь відзначали точки на координатній площині, з'єднали їх послідовно відрізками. Умова: х1 < х2

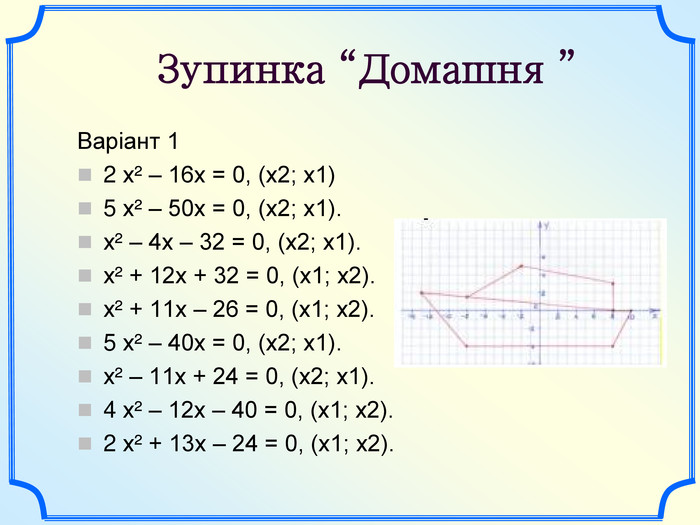
Слайд 3. Домашнє завдання.

 

2х² – 16х = 0 (х2; х1).

5х² – 50х = 0 (х2; х1).

х² – 4х – 32 = 0 (х2; х1).

х²+ 12х + 32 = 0 (х1; х2).

х²+ 11х – 26 = 0 (х1; х2).

5х²– 40х = 0 (х2; х1).

х² – 11х + 24 = 0 (х2; х1).

4х² – 12х – 40 = 0 (х1; х2).

2х² + 13х – 24 = 0 (х1; х2).

2х² + 16х  = 0 (х1; х2).

х² – 12х + 27 = 0 (х2; х1).

2х² – 6х  – 56 = 0 (х2; х1).

х² + 9х + 20 = 0 (х1; х2).

х² + 8х  = 0 (х1; х2). 

х² – 14х + 40 = 0 (х1; х2).

3х²– 18х + 15 = 0 (х1; х2).

4х² – 24х + 32 = 0 (х1; х2).

х² – 3х + 2,25 = 0 (х1; х2).

 

Слайд 4. Розв’язання домашнього завдання. Варіант 1. Варіант 2.

 

 

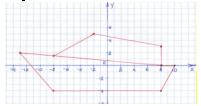
2-а зупинка: ЗАПРОШЕННЯ

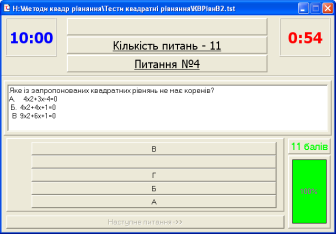
Тест. Якщо ви відповіли правильно на питання, то виставляєте собі 1 бал, якщо ні, то 0 балів.

 

 

3-я зупинка: ЗНАННЯ

Тест. А починаємо ми з питань теорії. Виберіть із запропонованих відповідей на питання правильну і запишіть його в заліковий лист під потрібною буквою в код відповідей.

 

Одночасно ми перевірятимемо відповіді. Якщо ви відповіли правильно на питання, то виставляєте собі 1 бал, якщо ні, то 0 балів.

 

1. Рівняння, що зводяться до вигляду ах²+вх+с=0, де а, в, з деякі числа, х- змінна, причому а<>0, називається .. рівнянням.

а) лінійним   б) квадратним в) дробово - раціональним

 

2. Квадратне рівняння, у якого коефіцієнт а=1 називається.

а) повним  б) зведеним   в) неповним  г) незведеним

 

3. Квадратне рівняння, у якого коефіцієнти в=0 або с=0 називається.

а) повним  б) зведеним  в) неповним  г) незведеним

 

4. Формула дискримінанта

а) Д= в– 4ас   б) Д= в²- 4ас  в )Д = в²- 4а.

 

5. Формула коренів квадратного рівняння:

а) х1= х2=  б) х1= х2=   в) х1= х2=

 

6. Якщо Д=0, то рівняння має

а) 2 корені   б) 1 корінь в) не має коренів

 

7. Якщо Д>0, то рівняння має

а) 2 корені   б) 1 корінь  в) не має коренів

 

8. Якщо Д<0, то рівняння має

а) 2 корені   б) 1 корінь в) не має коренів

 

9. Якщо а+в+с=0, то

а) х1=1, х2=с:а   б) х1= -1, х2=с:а  г) х1=-1, х2= -с:а

 

10. Якщо а-в+с=0, то

а) х1= -1, х2=с:а   б) х1= -1, х2= -с:а   в) х1=1, х2= -с:а

г) х1=1, х2= с:а

 

11. За теоремою Вієта сума коренів рівняння х²+рх+q=0 дорівнює

а) р   б) q    в) -q   г) – р

 

12. За теоремою Вієта добуток коренів рівняння х²+рх+q=0 дорівнює

а) р   б) q   в) -q  г) – р

 

4-а зупинка: МІРКУВАННЯ. ( I група комп’ютерне тестування.)

Підберіть для вказаних рівнянь найбільш раціональний спосіб розв’язання. Пояснити свій вибір.

1)х²-2х+1=0

2)х²-6х-7=0

3)х²-6х+3=0

4)х²+2х-35=0

5)х²+7х-18=0

 

5-а зупинка: ЗНАХІДКА ( II група комп’ютерне тестування.)

Тест. З теорією ми справилися. Подивимося, як у нас йдуть справи з практикою. Я пропоную тест. Відповідайте на питання до рівнянь, які подано на слайді.

 

Якщо ви відповіли правильно на питання тесту, то в код відповідей виставляєте собі 1 бал, якщо ні – 0 балів.

1. Виберіть рівняння, які не є квадратними.   (В1 – 7, В2 – 5)

 

2. Виберіть неповні квадратні рівняння.  (В1 – 5 і 6, В2 – 2 і 9)

 

3. Виберіть повні зведені квадратні рівняння.  (В1 – 3 і 4, В2 – 7 і 8)

 

4. Виберіть рівняння, у якого старший коефіцієнт дорівнює 5.  (В1 – 1, В2 – 4)

 

5. Виберіть рівняння, у якого другий коефіцієнт дорівнює -3. (В1 – 3, В2 – 7)

 

6. Виберіть квадратне рівняння, у якого вільний член дорівнює -5. (В1 – 2, В2 – 3)

 

7. Яке зведене квадратне рівняня не має коренів?  (В1 – 3, В2 – 7)

 

8. Дискримінант якого повного незведеного квадратного рівняння дорівнює 25? (В1 – 8, В2 – 6)

 

9. Яке з повних квадратних рівнянь можна вирішити, застосувавши властивості коефіцієнтів?

 

(В1 – 2 і 9, В2 – 8 і 6)

 

10. Сума коренів якого зведеного рівняння дорівнює 5?  (В1 – 4, В2 – 8)

 

11. Добуток коренів якого зведеного рівняння дорівнює 0?  (В1 – 6, В2 – 9)

 

12. Корені якого неповного рівняння дорівнюють 1 і -1? (В1 – 2, В2 – 2)

 

6-а зупинка: ІСТОРІЯ ( III група комп’ютерне тестування.)

  Розв’язати рівняння найбільш раціональним способом. Пояснити свій вибір.

Група 1                                                                   Група 2

Розв’язати рівняння  раціональним способом  Розв’язати рівняння раціональним способом

а) х²+15х=0                                                             а) -5х²+4х=0

б) 5х²-25=0                                                             б) 7х²-49=0

в) -9х+5х²=2                                                             в) 7х+2х²=-3

г) 2х²+4х=6                                                          г) 5х²+2х=3

д) 2х²-9=7х                                                            д) 3х²+2=5х

 

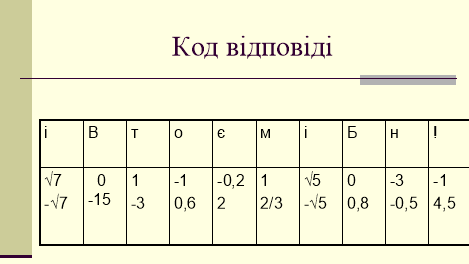
Якщо ви розв’язали рівняння, подивіться на таблицю-код. Складіть слово і запишіть в свій заліковий лист.

1В – Вієт!              2В – Біном

За кожну правильну знайдену букву нарахуйте собі 2 бали, за неправильну відповідь – 0 балів

і	В	т	о	є	м	і	Б	н	!
√7 -√7	0     -15	1 -3	-1 0,6	-0,2 2	1 2/3	√5 -√5	0 0,8	-3 -0,5	-1 4,5

 

Вчитель: Пригадайте, будь ласка, які способи розв’язання квадратних рівнянь ви знаєте.

 

Учні: 1) виділенням квадрата двочлена;     2) по формулі D;

 

3) по формулі через D1(формула з парним 2-м коефіцієнтом);

4) по властивостях коефіцієнтів;

5) за теоремою, оберненою до теореми Вієта.

Робота в групах. Учні складають план розв’язання рівнянь і розв’язують їх.

 

7-а зупинка: «ВМІННЯ»

Розв’язати  рівняння різними способами.

х² + 6х +5 =0             I група

 х² + 6х -7 =0             II група

 х² -7х +6 =0               III група

Дошка розмічена таким чином:

Виділення квадрата

Через D

Через D1

Властивості коефіцієнтів

По теоремі, оберненій теоремі Вієта

 Відповіді до завдань груп:I , II і III

Аналіз результатів.

Вчитель: Який же спосіб розв’язання є найбільш раціональним для даного рівняння?

 

Учні: Найбільш раціональне розв’язання – використання властивості коефіцієнтів.

 

 Підсумок уроку.

Сьогодні на уроці ми з вами повторили і узагальнили знання по темі «Квадратні рівняння».

Подивимося результати вашої роботи. Оцінку за активність роботи на уроці виставляє вам ваш сусід.

Рейтинг найбільш успішних учнів: 1..  2.  3.  4. 5.

(Оцінні листи зібрати).

 

Домашнє завдання.   Повторити теорію по записах в зошитах, п.п.    .

Розв’язати рівняння 3х² + 2х – 1 = 0 різними способами (10 способів).

Закінчити наш урок я хотіла б словами: Навчився сам, навчи іншого.

Домашня		Кількість балів
Запрошення
Знання
Міркування
Знахідка
Історія
Вміння
Активність на уроці
Підсумок

 

Релаксація уроку. Давайте поставимо загальну оцінку за урок. З яким настроєм ви йдете з уроку? Вибрати те лице, яке, на-вашу думку, відповідає вашому настрою.

 

 

 

 

 

Комп’ютерне тестування

«Квадратні рівняння»

 

 

 

 

 

 

 

 

 

КВИТОК НА ПОТЯГ «Долина - Київ»

Шановний пасажир___________________________________________________

Ми раді тебе вітати на потягу Знань! Тебе чекає захоплива подорож! Будь уважним, читай наші інструкції. Бажаємо приємно і з користю провести час в дорозі!

 

1-а зупинка: ДОМАШНЯ

Правильні 9 точок – «12».

Правильні 8 – 7 точок – «9».

Правильні 6 – 5 точок – «6».

 

2-а зупинка: ЗАПРОШЕННЯ

Тест. Якщо ви відповіли правильно на питання, то виставляєте собі 1 бал, якщо ні, то 0 балів.

 

3-я зупинка: ЗНАННЯ

Тест. Якщо ти відповів правильно на питання тесту, то в код відповідей виставляй собі 1 бал, якщо ні – 0 балів.

 

4-а зупинка: МІРКУВАННЯ.

Підберіть для вказаних рівнянь найбільш раціональний спосіб розв’язання. Пояснити свій вибір.

1)х²-2х+1=0

2)х²-6х-7=0

3)х²-6х+3=0

4)х²+2х-35=0

5)х²+7х-18=0

 

5-а зупинка: ЗНАХІДКА

Тест.

1. Виберіть рівняння, які не є квадратними.  

2. Виберіть неповні квадратні рівняння. 

3. Виберіть повні зведені квадратні рівняння. 

4. Виберіть рівняння, у якого старший коефіцієнт дорівнює 5. 

5. Виберіть рівняння, у якого другий коефіцієнт дорівнює -3.

6. Виберіть квадратне рівняння, у якого вільний член дорівнює -5.

7. Яке зведене квадратне рівняня не має коренів? 

8. Дискримінант якого повного незведеного квадратного рівняння дорівнює 25?

9. Яке з повних квадратних рівнянь можна вирішити, застосувавши властивості коефіцієнтів?

10. Сума коренів якого зведеного рівняння дорівнює 5? 

11. Добуток коренів якого зведеного рівняння дорівнює 0? 

12. Корені якого неповного рівняння дорівнюють 1 і -1?

 

 

6-а зупинка: ІСТОРІЯ

За кожну правильну знайдену букву нарахуйте собі 2 бали, за неправильну відповідь – 0 балів.

Група 1                                                                   Група 2

Розв’язати рівняння  раціональним способом  Розв’язати рівняння раціональним способом

а) х²+15х=0                                                             а) -5х²+4х=0

б) 5х²-25=0                                                             б) 7х²-49=0

в) -9х+5х²=2                                                             в) 7х+2х²=-3

г) 2х²+4х=6                                                          г) 5х²+2х=3

д) 2х²-9=7х                                                            д) 3х²+2=5х

Якщо ви розв’язали рівняння, подивіться на таблицю-код. Складіть слово і запишіть в свій заліковий лист.

 

і	В	т	о	є	м	і	Б	н	!
√7 -√7	0     -15	1 -3	-1 0,6	-0,2 2	1 2/3	√5 -√5	0 0,8	-3 -0,5	-1 4,5

 

7-а зупинка: «ВМІННЯ»

Розв’язати  рівняння різними способами.

х² + 6х +5 =0             I група

 х² + 6х -7 =0             II група

 х² -7х +6 =0               III група

Виділення квадрата

Через D

Через D1

Властивості коефіцієнтів

По теоремі, оберненій теоремі Вієта

 

Домашнє завдання. Повторити теорію по записах на довідкових листах.

Розв’язати рівняння 3х² + 2х – 1 = 0 різними способами (10 способів).

 

	Коди відповіді	Кількість балів
Домашня
Запрошення
Знання
Міркування
Знахідка
Історія
Вміння
Активність на уроці
Всього

 

З яким настроєм ви йдете з уроку?

 

Вибрати те лице, яке, на-вашу думку, відповідає вашому настрою