Квадратні рівняння. Формули коренів квадратного рівняння

Тема. Формула коренів квадратного рівняння

Мета: Розширити та поглибити знання про розв’язання квадратних рівнянь; вивести і засвоїти формули для розв'язування квадратних рівнянь; розвивати вміння правильно та послідовно міркувати; виховувати самостійність, цілеспрямованість, сміливість, організованість.

Тип уроку: комбінований.

Наочність та обладнання: опорний конспект «Квадратні рівняння», мультимедійне обладнання, картки з завданнями.

Хід уроку

1. Організаційний етап (слайд 1)

Вітаю всіх на уроці математики і вас, діти, і наших гостей. Сьогодні ми з вами вирушаємо у подорож по цікавій країні алгебра, з багажем знань і витримкою та наполегливістю.

Оголошення теми та мети уроку (слайд 2)

Антична мудрість говорить: «Знання – це сила», на мою думку знання – це одна із сходинок до успіху. І напевно, кожний із вас зрозумів, що для того щоб досягти успіху, потрібно багато працювати. Тому епіграфом нашого сьогоднішнього уроку нехай будуть слова англійського письменника Бернарда Шоу «Єдиний шлях, що веде до знань - діяльність» (слайд 3)

Я вам хочу побажати впевненості , творчої роботи та гарного настрою на уроці, адже кожну справу, аби вона мала успіх, потрібно починати з позитивом. Я буду вашим помічником, а девізом уроку будуть слова  Оноре де Бальзака «Щоб дійти до мети, перш за все треба  йти». (слайд 4)

2. Актуалізація опорних знань учнів

Ми продовжуємо вивчати розділ «Квадратні рівняння»

На попередньому уроці ми вивчали з вами неповні квадратні рівняння та методи їх розв’язування. Давайте згадаємо деякі основні відомості про рівняння.

1.     Фронтальне опитування учнів (слайд 5)

•          Що називається рівнянням?
•          Що називається  коренем рівнянням?
•          Що означає розв’язати рівняння?
•          Які рівняння називають квадратними?
•          Як називають коефіцієнти  квадратного рівняння ах2+вх+с=0?
•          Які існують види квадратних рівнянь?
•          Яке квадратне рівняння називають зведеним?
•          Яке квадратне рівняння називають неповним?
•          Які існують види неповних рівнянь?  (слайд 6)  -- види неповних рівнянь

2.     Усні вправи (слайд 7)

Серед даних рівнянь назвати ті, які є квадратними. Назвати коефіцієнти квадратного рівняння. 

1. 3х²–27 = 0,      а = 3, в = 0, с = - 27
2. х³ + х²– 1= 0, 
3. 0,5х + 6 = 8,
4.  х²- 3х + 2 = 0,   а = 1, в = -3, с = 2
5. 20х - 5х² = 0  а = -5, в = 20, с = 0

3.     Відновити квадратне рівняння: (слайд 8). Розв’язати неповні квадратні рівняння.

Розв’язання – (слайд 9)

0 і -2

Немає розв’язку

0

2/3 і -2/3

0 і 4

4.     Визначити вид рівняння. Розв’язати неповні квадратні рівняння.

(Взаємоперевірка) (слайд 10)

Розв’язання – (слайд 11)  (0 і 5; 2 і -2; немає розв’язку)

ІІІ. Засвоєння знань

Учитель. Ми  навчилися розв’язувати неповні квадратні рівняння.  А як же розв’язувати повні квадратні рівняння?

Формулювання проблеми: не­обхідно знайти єдиний достатньо простий алгоритм розв'язання квад­ратних рівнянь загального вигляду. Розв'язання цієї проблеми і є голов­ною метою уроку.

(слайд 12)

 Виведемо формулу коренів квадратного рівняння ах² + bх + с = 0.

Помножимо обидві частини рівняння на 4а (а ≠ 0), матимемо:

4а²х² + 4аbх+ 4ас = 0,

(2ах)² + 2∙2ах∙b + b² – b² + 4ас = 0,

(2ах + b)² – b² + 4ас = 0,

(2ах + b)² = b² – 4ас.

      Вираз  b² – 4ас називають дискримінантом (від латинського diskriminns – той, що розрізняє) даного рівняння і позначають буквою D. Тоді  (2ах + b)²  = D. За значенням D можна визначити кількість коренів квадратного рівняння ах² + bх + с = 0. (слайд 13)

1) Якщо D > 0, то   х₁ =  ;         х₂ =.

2) Якщо D = 0, то х =  –   – єдиний корінь.

3)  Якщо D < 0, то дане рівняння не має коренів.

ІV. Формування вмінь

Виконання усних вправ

1. (слайд 14) (1-ні, 2-так, 3-ні, 4-так)

2. (слайд 15) (1-немає коренів, 2- два корені, 3- один корінь)

Алгоритм розв’язування квадратних рівнянь за формулами (слайд 16)

1. Для рівняння записати значення а, b, с.
2. Обчислити дискримінант квадратного рівняння за формулою

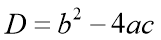
3. Визначивши знак дискримінанту, знайти кількість коренів та записати відповідну формулу його коренів  

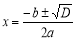
або  

4. Обчислити значення коренів квадратного рівняння.

5. Записати відповідь.

Виконання письмових вправ

1. Розв’язуємо квадратні рівняння разом (слайд 17, 18, 19)           

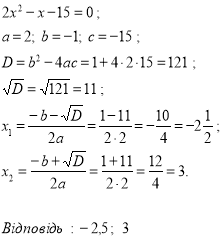
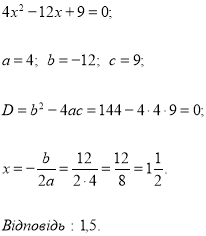
2. Розв’язати рівняння за формулами і скласти слово (прізвище відомого математика) (слайд 20)

Г)  2х² – 3х – 5 = 0.

(слайд 21)

Франсуа Вієт (слайд 22)

Історична довідка про квадратні рівняння

(слайд 23-26)

3. Самостійна робота (робота з підручником) (слайд 27)

№ 634 (розв’язати рівняння). Кожен учень розв’язує рівняння, номер якого співпадає з порядковим номером учня у списку класу. (Перевірка за зразком).

V. Підсумки уроку

«Знайди пару» (робота в парах) (слайд 28)

Давайте ще раз повторимо теоретичні відомості про квадратні рівняння.

Учням на кожну парту видаються  пронумеровані картки, на яких  закодовані початки означень і  картки, закодовані буквами, на яких  продовження цих означень. Потрібно з’єднати початок і кінець фрази в  одне речення. (Закодоване слово «ДИСКРИМІНАНТ»). Після виконання завдання учні  зачитують утворені фрази.

Учитель. Сьогодні на уроці ми пригадали з вами теоретичний матеріал по даній темі, навчилися застосовувати набуті знання й вміння в різних ситуаціях. Ви мали можливість удосконалити свої знання по темі «Квадратні рівняння». Наш урок я б хотіла закінчити словами: (слайд 29)

Рівняння – це не просто рівність

З однією змінною чи кількома.

Рівняння – це думок активність,

Це інтелекту боротьба.

То ж будьте творчими, активно розвивайтесь,

Долайте труднощі у своєму житті,

Але з рівняннями, прошу, не розлучайтесь,

Вони послужать вам ще в майбутті.

VI. Домашнє завдання (слайд 30)

1. Вивчити формули коренів квадратного рівняння.
2. Вивчити § 19
3. Виконати № 633, 635 (1-6)

Дякую за співпрацю і до зустрічі !  (слайд 31)