Сіваш В.В.

 

 

 

 

 

 

 

 

 

 

Песець – 2018 р.

ПЛАН

1.   Вступ

2.   Квадратні рівняння і їх розв’язання

2.1.   Означення квадратного рівняння

2.2.   Види квадратних рівнянь

2.3.Неповні квадратні рівняння

2.4.Зведене квадратне рівняння

2.5.Формула коренів квадратного рівняння загального виду

2.6.Розв’язування рівнянь за формулою

2.7.Графічне розв’язування квадратних рівнянь

3.   Теорема Вієта

3.1.   Теорема Вієта і обернена до неї

3.2.Розкладання на множники квадратного тричлена

4.   Рівняння і системи рівнянь що зводяться до квадратних

4.1.   Дробові рівняння

4.2.   Системи рівнянь другого степеня

5.   Задачі на складання квадратних рівнянь

5.1.   Способи розв’язування задач

5.2.   Задачі з буквеними даними

6.   Висновок

7.   Список використаної літератури

1. ВСТУП

Вивченню рівнянь присвячена значна частина всього навчального часу. Особлива значимість цієї теми полягає в широкому застосуванні рівнянь в найрізноманітніших галузях застосування математики.

Способи розв’язування деяки видів квадратних рівнянь з числовими коефіцієнтами були відомі ще за 1500 років до н.е. У творі «Начала» давньогрецького математика Евкліда разом з геометричним матеріалом містяться і задачі на квадратні рівняння, зокрема розв’язання задачі про «золотий переріз».

Неповні квадратні рівняння і окремі види повних квадратних рівнянь (х² ± х = а) вміли розв'язувати вавілоняни (близько 2 тис. років до н.е.). Про це свідчать знайдені клинописні тексти задач з розв'язаннями (у вигляді рецептів). Деякі види квадратних рівнянь, розв'язок яких зводиться до геометричних побудов, вміли ров'язувати старогрецькі математики. Приклади розв'язування рівнянь без звертання до геометрії дає Діофант Александрійський (III ст.). В шести з 13 книг «Арифметика», що дійшли до нас, містяться задачі з розв'язками, в яких Діофант пояснює, як треба вибрати невідоме, щоб дістати розв'язок рівняння виду ах = b або ах² = b. Спосіб розв'язування повних квадратних рівнянь Діофант виклав у книжках «Арифметика», які не збереглися.

Правило розв'язування квадратних рівнянь, зведених до виду ах² + bх = =с,. де а > 0, сформулював індійський вчений Брахмагупта (VII ст.). У трактаті «Китаб аль-джебр валь-мука-бала» хорезмський математик альХорезмі пояснює прийоми розв'язування рівнянь виду ах² = bх, ах² = с, ах = с, ах² + с= = bх, ах² + bх = с, bх + с = ах² (буквами а, b і с позначено лише додатні числа) і знаходить лише додатні корені.

Загальне правило розв'язування квадратних рівнянь, зведених до виду х² + bх = с, сформулював німецький математик М. Штіфель (1487—1567). Виводом формули розв'язування квадратних рівнянь загального виду займався Вієт. Проте своє твердження він висловлював лише для додатних коренів (від'ємних чисел він не визнавав). Після праць нідерландського математика А. Жірара (1595—1632), а також Декарта і Ньютона спосіб розв'язування квадратних рівнянь набув сучасного вигляду.

Формули, які виражають залежність коренів рівняння від його коефіцієнтів, ввів Вієт у 1591 р. Для квадратного рівняння теорема Вієта в сучасних позначеннях мала такий вигляд: коренями рівняння (а + b)х — х² = =аb є числа а і b. 

За сучасною шкільною програмою тему «Квадратні рівняння» вивчають у 8-му класі. Розглядати цей розділ треба за принципом: «Від найпростішого до складного». Це дає змогу учням краще та швидше засвоювати навчальний матеріал.

 

2.  КВАДРАТНІ РІВНЯННЯ І ЇХ РОЗВ’ЯЗУВАННЯ

 

2.1 Означення квадратного рівняння  У методичній літературі є багато різних означень поняття «квадратне рівняння». Найбільш поширені три типи означень. До першого типу можна віднести такі: «Рівняння називається квадратним, якщо найвищий   показник  степеня при невідомому дорівнює двом» .

Це означення неправильне, бо його задовольняє, наприклад, рівняння

                                                                                                        ²          3

x     7 x

яке, зрозуміло, не можна віднести до квадратних.

До другого типу означень віднесемо ті, в яких ототожнено поняття «квадратне рівняння» і «квадратне рівняння нормального виду»:

«Рівняння виду ах² + bх + с =0, де х — невідома величина, а, b, с — задані числа (а ≠ 0), називається квадратним» [1, 110].

Таке означення найбільш поширене. Але й воно має недоліки. Згідно з цим означенням рівняння  х² =3х + 5, х² - 5х + 7 =1, не квадратні. А як їх називати? Математики їх також відносять до квадратних рівнянь. Отже, треба давати інше означення. Саме цим і зумовлений третій тип означень.

«Рівняння, яке після перетворень можна звести до вигляду ах² + bх + с= = 0, де а, b, с — довільні числа і а ≠ 0, а х — невідоме, називається рівнянням другого степеня з одним невідомим, або, простіше, квадратним рівнянням»

[2, 286].

Проте й таке означення ми не можемо вважати вдалим, бо, наприклад, кожне з рівнянь

                                                                       10        x        x  2                              7

                                                                                                   , 2x     4x  8 

                                                                         x     x  2        x                           8

можна звести до вигляду ах² + bх + с = 0, але їх тепер не називають квадратними. Раніше, правда, і їх відносили до квадратних рівнянь. Квадратними називають тільки деякі цілих раціональних рівнянь; але ні дробових рівнянь, ні ірраціональних не бажано відносити до квадратних, хоч вони й можуть бути рівносильні деяким квадратним рівнянням.

Як бачимо, жодне з наведених вище означень квадратного рівняння не можна вважати бездоганним. Пізніше ми сформулюємо інші означення — одне для довільного квадратного рівняння, друге для квадратного рівняння нормального вигляду. А поки що зробимо ще одне зауваження. Не можна ототожнювати поняття «квадратне рівняння» і «рівняння другого степеня».

Рівняння другого степеня може мати два і більше невідомих. Наприклад, xy+5x-6y=7

— рівняння другого степеня відносно невідомих х і у. А квадратним його не називають. Квадратне рівняння — це рівняння другого степеня з одним невідомим.

Перед означенням квадратного рівняння доцільно з'ясувати поняття цілого алгебраїчного рівняння. Зробити це можна так.

— Рівняння, обидві частини якого — цілі алгебраїчні вирази, називається цілим алгебраїчним.

Приклади цілих алгебраїчних рівнянь:

x+3 = 7,  6с² + 1- 5с = 0,  х² - у=72.

Навпаки, рівняння

                                                                                              x 3              x

                                                                                              2  ,

                                                                                              x 3           x 3

не ціле, бо воно містить дробові вирази. Такі рівняння називають

дробовими.

Раніше ми розглядали цілі алгебраїчні рівняння, що містять невідоме тільки в першому степені. Але іноді доводиться розв'язувати і такі рівняння, що містять невідоме в другому степені. 

Задача. Одне з двох чисел більше від другого на 7, а добуток їх дорівнює 744. Знайти ці числа.

Розв’язання: Позначимо менше число буквою х. Тоді більше буде х + +7. Добуток цих чисел дорівнює х (х + 7). В задачі сказано, що добуток цих двох чисел дорівнює 744. Отже,

х (х + 7) = 744,  або х² + 7х = 744.

Дістали рівняння, що містить невідоме х і в першому, і в другому степені. Такі рівняння називають квадратними. В квадратному рівнянні всі члени з правої частини можна перенести в ліву (з протилежними знаками). Отже, кожне квадратне рівняння можна замінити рівносильним йому рівнянням виду ах² + bх + с =0,

де а, b і с — дані числа, коефіцієнти рівняння.

Коефіцієнти квадратного рівняння можуть бути цілими і дробовими, додатними і від'ємними. Коефіцієнти b і с можуть також дорівнювати нулю, але а не може дорівнювати нулю, бо інакше це рівняння не було б квадратним.

Приблизно таким          поясненням          підводимо учнів до      означення квадратного рівняння. А тепер вже можна сформулювати його: ціле рівняння з одним невідомим, яке після розкриття дужок, перенесення всіх членів у ліву частину і зведення подібних членів набирає вигляду ах² + bх + с = 0,

де а ≠ 0, b, с — довільні   числа, називається квадратним рівнянням.

Рівняння ах² + bх + с = 0 при а ≠ 0 називається квадратним рівнянням нормального виду.

Бажано після цього повторити з учнями ці означення, проілюструвати їх кількома конкретними прикладами і контрприкладами (див. [4, 33]), а вже потім перейти до розгляду квадратних рівнянь окремих видів.

2.2 Види квадратних рівнянь

У підручнику О. М. Барсукова насамперед говориться про квадратне рівняння нормального виду (при а≠0), а потім   відмічається:  «Надалі   для спрощення завжди припускатимемо, що а  >0» [3, 211].

Виходить, учні ознайомляться з квадратним рівнянням нормального виду, але далі розглядатимуть не його, а лише рівняння виду ах² + bх + с = 0 при додатному а, для якого немає спеціальної назви. Методично це незручно. Значно краще було б або називати квадратним рівнянням нормального виду рівняння ах² + bх + с = 0 при а > 0 і зауважити, що надалі розглядатимемо саме такі рівняння, або не обмежуватись розглядом таких рівнянь лише при додатних а. Очевидно, другий варіант кращий.

Навіщо накладають умову а > 0? Тільки для того, щоб не розглядати двох випадків, коли виводять формули коренів. Адже якщо виводити формулу коренів для рівняння ах² + bх + + с = 0 при а > 0, то можна писати:             

                                                                                 b             b²  4ac b b²  4ac

                                                                     x 2a            4a₂                2a           

А якби не наклали умову а > 0, то треба було б писати інакше:

                                                                                 b            b² 4ac b            b² 4ac

                                                                     x2a             4a₂  2a            2a       

 

Проте це не дуже важлива причина, бо перед останнім дробом стоїть подвійний знак ±, отже, і при додатному, і при від'ємному а дістанемо ту саму формулу    

b b² 4ac x

2a

До того ж цю формулу можна виводити й іншим способом, так, що не треба виносити а за знак радикала.

Ось чому не треба накладати умову а > 0, а розглядати в школі квадратне рівняння нормального виду ах² + bх + с = 0 при довільному а≠ 0.

Якщо в рівнянні ах² + bх + с = 0 хоч один з коефіцієнтів b або с дорівнює нулю, то таке квадратне рівняння називають неповним.

Розглядають три види неповних квадратних рівнянь:

ах² + bх = 0 — квадратне  рівняння без вільного члена; ах² + с = 0 — двочленне квадратне рівняння; ах² = 0 — одночленне квадратне рівняння.

Подібні терміни часто вживаються в курсі вищої алгебри для рівнянь nго степеня .

Щоб підкреслити, що дане квадратне рівняння не є неповним, вживають термін «повне квадратне рівняння». Так називають рівняння ах² + +bх + с = 0, в якому а≠0, b≠0, с≠0. Не треба протиставляти повному квадратному рівнянню зведене. Зведеним може бути і повне квадратне рівняння, і неповне (при а = 1). 

 

2.3  Неповні квадратні рівняння Починають звичайно з неповних квадратних рівнянь. Дають означення, показують, що неповних квадратних   рівнянь є три види,  і тільки після цього приступають до їх розв'язування. Розглядати їх найкраще в такій послідовності:

ах² + bх = 0,    ах² = 0,    ах² + с = 0.

Починати розгляд кожного виду краще з конкретного прикладу.

Приклад    1. Розв'язати рівняння 5х² + 4х = 0.

Розв’язання. Розклавши ліву частину цього рівняння на множники, дістанемо:

х (5х + 4) = 0.

Відомо, що добуток двох множників-многочленів дорівнює нулю, коли перший або другий з них дорівнює нулю. Маємо: або х = 0, або 5х + 4 = 0, звідки х = - 0,8.

Отже, дане рівняння має два корені: х = 0 і х = - 0,8. Пишуть також: х₁ = 0; х₂ = -0,8.

Перевірка.

1)  5·0² +4·0 = 0;   2) 5· (—0,8)²+ 4·(—0,8) = 3,2 - 3,2 = 0.

В і д п о в і д ь. х₁ = 0; х₂ = -0,8.

Варто таким самим способом розв'язати ще два рівняння з числовими коефіцієнтами, а потім узагальнити.

Так само можна розв'язати будь-яке квадратне рівняння виду ах² + bх = 0.

Розклавши ліву частину цього рівняння на множники, дістанемо: х(ах + b) = 0.

Прирівнявши спочатку перший, а потім другий множник де нуля, знайдемо:

1)       x = 0;

2)       ах + b = 0, звідки х =_ ^b . a

Отже, кожне рівняння виду ах² + bх = 0 має два корені: х₁= 0, х₂ =_ ^b . a Не всі, правда, з останнім висновком погоджуються. Іноді зазначають, що рівняння розглядуваного виду має два розв'язки тільки при b ≠ 0. Якщо ж b = 0, то дістанемо неповне квадратне рівняння виду ах² = 0, яке має тільки один корінь х = 0. Такого погляду дотримується багато методистів, у тому числі  М. Барсуков [3, 214]. Проте є й інші думки. Наприклад, В. В. Реп'єв

про рівняння ах² = 0 пише: «Оскільки а ≠ 0, то воно зводиться до рівносильного рівняння х² = 0. Звідси х₁ = 0 і х₂ = 0. Рівняння має два корені, кожний з яких дорівнює нулю» [5, 242].

Отже, одні автори підручників і посібників спочатку пояснюють, що рівняння ах² = 0 має тільки один корінь, а через кілька уроків зауважують: «Домовимось вважати, що рівняння ах² =  0 також має два корені: х₁ = 0 і х₂ = =0». Інші з самого початку пояснюють, що розглядуване рівняння має два рівних корені. З методичного і наукового погляду другі роблять краще.

Рівняння виду ах² + с = 0 спочатку бажано розглянути при а = 1, наприклад:

x²  - 4 = 0.

Ось як пропонують розв'язувати це рівняння деякі методисти.

«Наприклад, розв'язується рівняння х² = 4, х_1,2= ±2. Учні часто не розуміють, чому ±  ставлять тільки в правій   частині. Можна  пояснити на тому самому    прикладі х² = 4;   ±х = ±2. Це дає чотири комбінації знаків, які зведуться до двох: 

                                                                      x  2                   x  2

                                                                                        x₁  2                   x₁  2

                                                                      x  2_                   x  2_

Тому досить писати х_1,2= ±2» .

Цей метод розв'язування був досить поширений раніше, але він дуже невдалий, йдеться про таке розв'язання: «Добувши з обох частин рівняння х² = 4 квадратні корені, дістанемо ±х = ±2...». Тут багато незрозумілого. Поперше, яке ми маємо право добувати з обох частин рівняння квадратні корені? Ми ж раніше не доводили, що в результаті дістанемо рівняння, рівносильне даному, та цього й не можна довести. По-друге, чому саме добуваємо не арифметичні корені, а «алгебраїчні»? Учням це не зовсім зрозуміле. Нарешті, чому з рівності ±х = ±2 ми повинні виписати всі можливі чотири комбінації, а не брати окремо тільки верхні знаки, а потім тільки нижні? Наприклад, якщо з обох частин рівності 4 = 4 добути квадратні корені, то дістанемо ±2 = ±2, а звідси не випливає, що +2 = —2, і т. ін.

Ось чому  не рекомендується розв'язувати двочленні квадратні рівняння таким способом. Значно краще ліву частину такого рівняння розкласти на множники: x²  - 4 = 0, (x-2)(x+2)=0

Отже, х — 2 = 0, звідки х = 2, або х + 2 = 0, звідки х = —2.

Таким чином, дане рівняння має два корені: х₁ = 2, х₂ = —2. Можна пояснювати й так. Дане рівняння рівносильне такому: х² = 4. Треба знайти число х, квадрат якого дорівнює 4.  A  це означає, що треба знайти квадратний корінь з 4. Квадратних коренів з числа 4 є два: 2 і —2. Отже, рівняння має два корені:

х₁ = 2, х₂ = —2.

Тут другий спосіб здається гіршим від першого, але цим способом зручніше розглядати загальний випадок рівняння ах^г + с = 0. Перенесемо член с в праву частину і поділимо всі члени здобутого рівняння на а. В результаті дістанемо:

х2 = с a

Якщо а і с мають різні знаки (однe додатне, а друге від'ємне), то число

      с                                                                                                              с

_  додатне. Тоді х — число, квадрат якого дорівнює _ , тобто х дорівнює a   a

с квадратному кореню з числа  _. Таких квадратних коренів є два:   _  і a

 .

 У цьому випадку дане рівняння має два корені:

х₁=  , х₂= _

с

Якщо а і с мають однакові знаки, то число _  від'ємне. Добути a

квадратний корінь з від'ємного числа не можна. Тому в цьому випадку дане рівняння не має жодного розв'язку.

Отже, неповне квадратне рівняння виду ах² + с = 0 не має жодного розв'язку, якщо коефіцієнти а і с мають однакові знаки, а якщо їх знаки різні,

то це рівняння має два розв'язки: 

 Тільки тепер можна зауважити, що такі дві формули домовились об'єднувати в одну, вживаючи подвійний знак ±:

х1,2= _ .

2.4 Зведене квадратне рівняння

Програми пропонують зразу після неповних квадратних рівнянь розглянути зведені рівняння. Можливі два способи їх вивчення: 

1)                 зразу вивести формулу  коренів, а   потім,  користуючись нею, розв'язувати різні конкретні зведені квадратні  рівняння ;

2)                 почати  з розв'язування конкретних зведених рівнянь способом виділення повного квадрата, після чого учні самі зможуть вивести загальну формулу. Другий спосіб (його можна назвати конкретно-індуктивним) має багато переваг порівняно з першим. Шкільний задачник П. О. Ларічева також передбачає, що спочатку вчитель пропонуватиме учням  розв'язувати рівняння без формули, виділяючи повні квадрати двочленів.

Робити це можна так. Нехай треба розв'язати рівняння х² +8х — 33 = =0. Тут  х² — квадрат шуканого числа. 8х  можна розглядати як 2 · х · 4, тобто як подвоєний добуток першого числа на 4. Додамо й віднімемо 4²: х² +2 · х · 4 + 4² - 4² – 33 =0

Три перші доданки становлять квадрат суми чисел х і 4. Отже, здобуте рівняння можна записати так: 

(х + 4)²— 16 — 33 = 0,  або (х + 4)² —7²=0.

Розкладемо на множники різницю квадратів, що в лівій частині:

(х + 4 - 7)(х  + 4 +7) = 0,  або (х - 3)(х + 11) = 0

Бачимо, що добуток двох виразів дорівнює нулю. Це може бути, коли один або другий з них дорівнює нулю. Маємо:

х — 3 = 0, звідки х = 3, або  х + 11 = 0, звідки х = — 11.

Відповідь. Рівняння має два корені: х₁ = 3, х₂ = —11.

Зрозуміло, що, діставши рівняння (х + 4)²—16 — 33 = 0, далі можна розв'язувати інакше: (х + 4)² = 49.

Це — неповне квадратне рівняння виду z² = 49. Воно має розв'язки      z₁

= 7, z₂= —7. Отже, х + 4 = 7,  звідки х = 3,

або

х + 4 = — 7, звідки х = — 11.

Ці обидва прийоми розв'язання для учнів однаково зрозумілі.

Бажано, розв'язавши однe таке рівняння, виконати перевірку, а потім таким самим способом розв'язати ще кілька рівнянь. На наступному уроці можна зразу запропонувати учням розв'язати рівняння з буквеними коефіцієнтами  х² + рх + q = 0, тобто самостійно вивести формулу коренів для

зведеного квадратного рівняння:

х1,2=

2.5 Формула коренів квадратного рівняння загального виду

Формулу коренів квадратного рівняння загального виду  ах² +  bх + с = =0 (за умови, що b²—4ас≥0), можна виводити  багатьма різними виду          способами. Якщо перед цим розглядати, як пропонує діюча програма, зведене квадратне рівняння, то рівняння загального виду діленням на а (а≠0) можна замінити зведеним:

х ² + ^b + ^с = 0. a          a

Тоді, підставивши у формулу коренів зведеного рівняння р = ^b , q = ^с ,

aa

зразу дістанемо

bb²                  c х1,2= 2a 4a₂ _a .

звідки при а > 0

^b b² 4ac       b b² 4ac х₁= ,               х₂=

                                                                          2a                                                       2a

 

а при а < 0

b b² 4ac       b b² 4ac х₁=,               х₂=

                                                                          2a                                                       2a

В обох випадках маємо ті самі дві формули, які можна об'єднати в одну:

х1,2= b b2 4ac

2a Ця формула вірна при будь-яких а ≠ 0.

Зауважимо, що таке виведення формули можна давати учням тільки тоді, коли вони: 

1) знають формулу коренів зведеного квадратного рівняння  2) знають теорему про корінь з дробу. 

Але, як видно з нової програми, цих питань семикласники можуть не знати. Тоді доведеться пояснювати інакше.

Помноживши обидві частини  рівняння ах² + bх + с = 0 на 4а, дістанемо рівносильне йому рівняння: 

4а²x² + 4аbх + 4ас = 0,

4а²х² + 4аbх + b² — b²+4ас = 0, (2ах + b)² = b² — 4ас.

Тепер розглянемо два випадки.

1.        Якщо b² — 4ас > 0, то 2ах + b = ± b² 4ac , звідки

b b² 4ac

                                                                                       х1,2=                     

2a

 

2.        Якщо b² — 4ас < 0, то рівняння коренів не має.

Другий спосіб простіший. До того ж при таких міркуваннях відпадає потреба окремо розглядати випадки, коли а > 0 і коли а < 0. Тому цей спосіб можна вважати найкращим.

 

 

Скільки формул давати учням

Вище ми розглянули дві формули коренів квадратних рівнянь, а саме:

для рівняння х² + рх + q  =  0:  

                                                                              х_1,2=  q         (І)

і для рівняння ах² + bх + с = 0:

b b² 4ac

                                                                                               х_1,2=.                  (II)

2a

Багато методистів пропонують давати учням також формулу для рівняння ах² + 2kх + с= 0:

k k² 4ac

                                                                                             х_1,2=.                    (III)

a

У посібникуах, крім згаданих вище, пропонуються ще дві формули для зведеного і загального рівнянь відповідно:

                                                                               х1,2= p p2 4q ,           (IV)

2

                                                                             х1,2=         2c            .        (V)

bm b² 4ac

Постає питання: які з цих п'яти формул давати учням? Дві останні ніхто з методистів не рекомендує. Щодо трьох перших, погляди методистів значно розходяться. Раніше вимагали, щоб учні запам'ятовували всі три формули і користувалися формулою для коренів зведеного рівняння, коли а=1 i b парне; другою формулою, коли а — яке завгодно і b непарне;

третьою, коли а відмінне від 1 i b парне .

І в методиках, навіть найновіших, ідеться не про формулу коренів квадратного рівняння, а про «системи формул коренів квадратного рівняння». Навіщо давати учням цілу систему формул? Адже кожна  з  формул — така сама   загальна, як і інші, кожна з них придатна для розв'язування будь-якого квадратного рівняння. Чогось нового під час вивчення цієї системи формул учні не взнають. Навіщо ж ми намагаємося завантажити пам'ять учнів цілою системою формул для розв'язування однієї й тієї самої задачі? Відповідь одна: щоб зекономити кілька годин. Вважають, що одні рівняння швидше розв'язуються за першою формулою, інші — за другою і т. д. Все це правильно. Але дослідження показує, що в результаті використання багатьох формул виграш у часі не такий вже великий. Він не набагато перевищує час, потрібний для вивчення цих додаткових формул. А неприємностей при цьому трапляється багато. Коли учням пояснюють дві або три формули, то вони часто жодної не знають добре. У новій програмі також сказано, що учням слід давати тільки одну «загальну формулу розв'язку».

2.6  Розв’язування рівнянь за формулою

Після того як виведено загальну формулу коренів квадратного рівняння, всі такі рівняння слід розв'язувати за цією формулою. Оформляти записи можна по-різному. Спочатку доведеться писати все повністю, підставляючи  у формулу   замість кожної букви її значення. Але вже після двох-трьох таких вправ можна пропонувати учням деякі з проміжних обчислень виконувати усно і писати, наприклад, так:

1)       X² + 8X+ 12 = 0,

               _х1,2=  8   64  48 _  8  4 ,

                                            2                    2

х₁ = —2, х₂ = —6.

2)       2x² — 5x + 5 = 0,

_х1,2=5 2540 . 4

Розв'язків немає.

Можна рекомендувати також спочатку обчислювати дискримінант рівняння, наприклад:

71х²— 144x+ 73 = 0,

∆ = 144² — 4 · 71 · 73 = 4(72² — 71 · 73) = 4 [72² — (72²— 1)] = 4,

х1,2=,

x₁ = 1,  x₂ = ⁷³ .

71

Як видно з цього прикладу, в деяких випадках обчислення дискримінанта вдається спростити, використовуючи формули скороченого множення.

Бажано також показати учням раціональні способи перевірки знайдених розв'язків. Якщо, перевіряючи другий корінь, учень безпосередньо обчислюватиме  значення кожного члена многочлена, що стоїть у лівій частині рівняння, це забере багато часу і енергії. Краще робити так:

71 · ⁷³₂² - 144·        + 73 =         (73-144 + 71) = 0. 71

Ще краще спочатку поділити обидві частини даного рівняння на х

(адже x≠0) і перевіряти, чи задовольняють знайдені корені рівняння

71x — 144 + ⁷³  = 0, x

еквівалентне даному. Маємо:

71 ·  - 144 +  = 73-144 + 71 = 0.

Дещо інші форми запису пропонуються в посібнику [6, 260].

Вище йшлося про розв'язування квадратних рівнянь нормального виду. Але в школі доводиться розв'язувати більше таких рівнянь, які не зведені до нормального виду. Їх записують, наприклад, так:

                                                                                 (35x)²                     82x (x3)(x7)

                                                                     6x                                                      ,

                                                                                        2               5                  2

60x+5(9+30x+25x²)=2(8-2x)-5(x²+10x+21),

 

60x + 45 + 150x + 125x² = 16 — 4x — 5x² — 50x — 105,

130X² + 264x +134 = 0,

65x²+ 132x + 67 = 0,

∆ = 132²  - 4 · 65 · 67 = 4 (66²  - 65 · 67) = 4,

                                                                                _х1,2= 132    4 _  66 1 ,

                                                                                                    265              65

Відповідь: x₁ = — 1, x₂ =_  .  

Корисно показати учням, що за формулою для повного квадратного рівняння можна розв'язувати і неповні. Наприклад:

4x2 – 9 = 0, х1,2= 0       0  4 49  , 8

3x2 + 4x = 0, х1,2= 4 160  4 4 , х1=0, х2=

                                                                                                         6                  6

 

2.7 Графічне розв’язування квадратних рівнянь Діюча програма передбачає і графічне розв'язування квадратних рівнянь. Рівняння виду  x² + рх + q = 0

графічно можна розв’язувати так. Подаємо його у вигляді x² = — рх — q

і будуємо на одній координатній площині графіки функцій у =  х² і у = = —рх — q. Графіком першої функції є парабола, а другої — пряма. Абсциси точок перетину цих ліній будуть розв'язками даного рівняння, бо при цих значеннях x вирази х² і —рх — q рівні між собою.

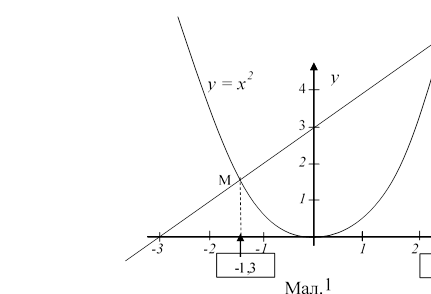
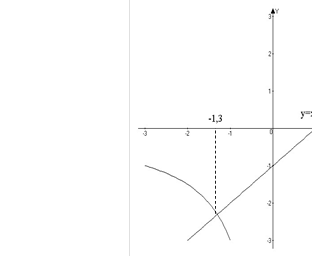
Приклад. Розв'язати  графічно рівняння  x² — x — 3 = 0.

Розв'язання. x² = x + 3. Будуємо графіки функцій і y = x + 3.

Вони перетинаються в точках М і N (мал. 93), абсциси яких x₁≈—1,3 і x₂≈2,3.

Це і будуть наближені значення коренів даного рівняння.

Перевірку можна зробити, безпосередньо підставивши здобуті значення x у дане рівняння:

(-1,3)²— (-1,3) — 3=1,69+ 1,3 —3 = —0,01; 2,3² —2,3 —3 = 5,29 —2,3 —3 = —0,01.

Але можна розв'язати дане рівняння за відомою формулою і потім

обчислити знайдені корені:  х 1,303 і x2≈2,303.

Зрозуміло (і це можна сказати учням), що ніхто з математиків  квадратних рівнянь не розв'язує графічно,  бо за  відомими формулами їх можна розв'язувати і швидше і точніше. Тому багато рівнянь цим способом розв'язувати не треба. Але на двох-трьох прикладах бажано ознайомити учнів з цим способом. При розв'язуванні інших рівнянь він буває дуже зручним і навіть єдино можливим.

Не треба думати, що, розв'язуючи таке рівняння графічно, слід будувати графіки функцій у=x² і у=—рх — q. Рівняння x² + рх + q = 0 можна переписати і так: x² + рх = —q. Тому досить на одній координатній площині побудувати графіки функцій у = x² + рх і у = —q. Можна рівняння переписати і так: х² + q = —рх. У цьому разі на координатній площині треба побудувати графіки функцій у = x² + q і у = —рх. У кожному випадку абсциси точок перетину дорівнюватимуть (наближено) кореням даного рівняння.

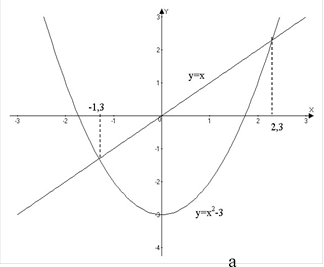
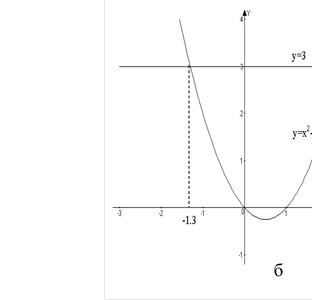
На мал. 2 показано розв'язання рівняння х² — x — 3 = 0 двома іншими прийомами.

 

                                                                    

                                                            Мал.2.

 

Нарешті, обидві частини даного рівняння можна поділити на x (бо х≠

0). Тоді дістанемо рівняння x—1= ³ , рівносильне даному. Графічне x

розв'язування його  зводиться до побудови прямої  у = х — 1 і  гіперболи у =

=1 (мал. 3). Найкращий з описаних вище прийомів перший.

 

 

 

 

 

 

Мал. 3

 

 

Відомий  і такий спосіб розв'язування квадратних рівнянь. Щоб розв язати рівняння х² + рх + q = 0, досить провести коло з центром у точці С

( ^{p ; q 1}) яке проходило б через точку М (0; 1). Це коло перетинає вісь ОХ у

        2      2

точках, абсциси яких дорівнюють кореням даного рівняння. На мал. 4 і 5 таким способом розв'язано рівняння х² —  4x +3 =0  i x² – 2x – 5 = 0.

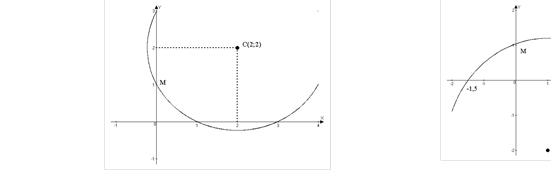
                                Мал. 4                                                    Мал. 5

Цей спосіб розв'язування квадратних рівнянь можна розглянути на математичному гуртку. Обгрунтування його нескладне, учні самі можуть з ним справитись. 

 

3. ТЕОРЕМА ВІЄТА

 

3.1. Теорема Вієта і обернена до неї

Найчастіше формулюють і використовують теорему Вієта для зведеного квадратного рівняння.

Підвести учнів до цієї теореми краще на конкретних прикладах. Можна запропонувати таку вправу:

«Визначити суму і добуток коренів рівнянь: 1) х² —5х+6 = 0; 2) х² + 3х — 4 = 0».

Після розв'язання вправи можна записати на дошці: х² — 5х + 6 = 0, х₁ + х₂= 5, х₁ х₂ = 6. x² + 3х — 4 = 0,   х₁ + х₂ = —3, х₁ х₂ = —4.

Цей запис безперечно спонукає учнів задуматися. Учителеві варто запитати, що помітили учні на розглянутих прикладах, запропонувати сформулювати гіпотезу, перевірити цю гіпотезу ще на одному рівнянні, наприклад х² — 3х—10 = 0, а потім запропонувати довести теорему в загальному вигляді.

Запишіть формули коренів рівняння х² + рх + q = 0 і додайте їх. Що дістали? Правильно, —р. А тепер помножте ці формули...

На дошці бажано записати:

х² + рх + q = 0,   х₁+ х₂ = —р, х₁ х₂ = q.

Після того як учні запам'ятають формулювання теореми і зрозуміють її доведення, слід повідомити, що цю теорему вперше довів у 1591 р. французький математик Франсуа Вієт (1540—1603). Його біографія досить цікава і повчальна, тому бажано коротко і її розповісти учням, зокрема, бажано відмітити, що іспанська інквізиція заочно приговорила його до спалення на вогнищі.

Сам Вієт цю теорему формулював інакше: «Якщо В + D, помножене на А, мінус А² дорівнює ВD, то А дорівнює В і дорівнює D». Але семикласникам про це краще не говорити, бо вони не зрозуміють, який зміст вкладали раніше в це речення.

                Теорему     Вієта     не     треба     ототожнювати     з     оберненою     їй.

Теорема Вієта  Обернена теорема

Якщо x₁ i x₂ – корені рів-Якщо х₁+ х₂ = —р,  х₁  х₂ = q, то няння х² + рх + q = 0, то  числа х₁ і   х₂ – корені рівняння х₁+ х₂ = —р,  х₁  х₂ = q. х² + рх + q = 0.

Чи треба пояснювати учням обернену теорему? У «Методиці

викладання алгебри» К. С. Барибіна сказано, що у VIII класі її розглядати не варто [3, 266]. Проте з цим не можна погодитись. Обернена теорема частіше використовується, ніж пряма. Тому не випадково вивчення оберненої теореми передбачене новою програмою. У підручнику [4, 229] доведено також обернену теорему.

Можна запропонувати й таке доведення оберненої теореми.

Д а н о.  x₁ + х₂ = — р і х₁  х₂ = q.

Д о в є с т и. х₁  х₂ — корені рівняння х² + рх + q = 0.

Доведення. З першої рівності маємо х₂ = — р — х₁. Підставимо - р - х₁

замість х₂ в другу з даних рівностей:

х₁ (-p - х₁ ) = q , звідки х₁² + рх₁ + q = 0.

Отже, х₁ — корінь рівняння х² + рх + q = 0. Якщо з першої рівності

знайдемо  х₁ і підставимо значення його в другу рівність, то дістанемо  х₂(-p – х₂ ) = q , звідки х₂² + рх₂ + q = 0.

A це означає, що і число х₂ є коренем рівняння х² + рх + q = 0.

Після доведення теореми бажано запропонувати учням такі задачі:

«Довести, що коли один корінь рівняння х² + рх + q = 0 є с, то другий корінь дорівнює -р - с».

«Довести, що коли один корінь рівняння х² + рх + q = 0 є с, то другий

корінь дорівнює ^q ».

c

Це дуже легкі задачі, сформульовані в них твердження безпосередньо випливають з теореми Вієта.

Бажано показати учням, як, користуючись теоремою Вієта, можна перевірити правильність розв'язання квадратного рівняння. Наприклад, розв'язавши рівняння х² - 6,5x + 9 = 0, дістали x₁ = 4,5; х₂ = 2. Перевірити, чи правильно розв'язано рівняння, можна так:

4,5 + 2 = 6,5; 4,5 · 2 = 9.

Дістали другий коефіцієнт з протилежним знаком і вільний член. Значить, рівняння розв'язано правильно. Користуючись теоремою Вієта, деякі зведені квадратні рівняння можна розв'язувати усно. Нехай, наприклад, треба розв'язати рівняння

х² - 5х + 6 = 0.

Добуток його коренів дорівнює 6, а їх сума дорівнює 5. Неважко догадатись, що це числа 2  і 3. Отже, х₁ = 2;  х₂ = 3.

Теорему, обернену до теореми Вієта, можна використовувати і при розв'язуванні вправ на складання квадратних рівнянь за даними коренями.

Приклад 1. Скласти квадратне рівняння за даними його коренями 2 і 3.

Розв'язання.

— р = 2 + 3 = 5,   q = 2 • 3 = 6.

Шукане рівняння таке: х² — 5х + 6 = 0.

Пізніше можна буде пояснити учням, як такі задачі розв'язувати іншим способом. A тепер треба зауважити, що сформульована вище задача взагалі невизначена. Ми склали одне рівняння, що має корені 2 і 3, а таких квадратних рівнянь існує безліч:

2х² — 10x + 12 = 0,  0,5х² — 2,5x + 3 = 0 і т.д.

Щоб позбутися цієї невизначеності, формулювання задачі можна уточнити: «Скласти зведене квадратне рівняння за даними його коренями 2 і 3» або «Скласти квадратне рівняння за даними його коренями 2 і 3, щоб його перший коефіцієнт дорівнював 5».

У шкільному збірнику є багато і таких вправ, в яких вимагається скласти квадратне рівняння, корені якого були б зв'язані певною залежністю з коренями іншого рівняння.

Приклад 2. Не розв'язуючи даного рівняння, скласти квадратне рівняння, корені якого були б на 5 більші за корені рівняння х² + 6х + 8 = 0. Розв'язання. Нехай корені даного рівняння x₁ і  х_2;   x₁ +  х₂= —6, x₁ х₂= 8.

Корені шуканого рівняння на 5 більші від коренів даного, тобто  z₁ = x₁ + 5, z₂ = х₂ + 5.

Отже,

— р = z₁ + z₂ = х₁ + х₂ + 10 = — 6 + 10 = 4, q =  z₁ z₂ = (х₁ + 5) (х₂ + 5) = х₁ х₂ + 5 (х₁+ х₂) + 25 = 3.

Відповідь: z² — 4z + 3 = 0.

Приклад 3. Не розв'язуючи рівняння х² — рх + q = 0, скласти квадратне рівняння, корені якого були б обернені до коренів даного. 

Розв'язання. Нехай корені даного рівняння х₁, х₂.  Тоді за теоремою Вієта х₁+ х₂ = р, х₁ х₂ = q.

Позначимо   корені   шуканого   рівняння   через z₁ і  z₂. Тоді

z₁ = ¹ ,  z₂ = ¹ x1          x2

Через це

z1+ z2= 1 + 1 = x1 x2 = p , x1                x2     x1x2            q z1 z2= 1 = 1 .

                                                                                                             x1x2            q

Маємо шукане рівняння:

z² - ^p z + ¹ = 0 z          q

або

q z² – p z + 1=0

 

3.2  Розкладання на множники квадратного тричлена

Кілька вправ, що зводяться до розкладання на множники, можна розв’язати з учнями ще під час вивчення теми «Розкладання многочленів на множники». При цьому замінюють якийсь член алгебраїчною сумою двох одночленів. Найчастіше замінюють середній член, наприклад: х² +7х + 6 = х² + х + 6x + 6 = x(x+1) + 6(x+1) = (x+1)(x+6)

Але можна замінювати й інші члени:

х² +7х + 6  = 7х²  - 6 х² +7 х +  6 =7 x(x+1) - 6(x²-1) = (x+1)(x+6)

Поки учні ще не вміють розв'язувати квадратних рівнянь, такі вправи досить важкі для них, тому їх можна пропонувати тільки сильнішим. Коли ж вони навчаться розв'язувати квадратні рівняння і знатимуть теорему Вієта, такі вправи можна розв'язувати за досить простим алгоритмом, і їх повинні вміти розв'язувати всі.

Пояснення нового матеріалу бажано оформити у вигляді теореми. Якщо х₁ і х₂ — корені тричлена х² + рх + q, то вірна тотожність х² + рх + q  = (х — х₁) (х — х₂).

 Доведення. Якщо х₁ і х₂ — корені тричлена х² + рх + q, то за теоремою

Вієта р = — х₁ — х₂, q= х₁ х₂. Тому 

х² + рх + q = х² +  х (—х₁ — х₂) +  х₁ х₂ = х² — х₁х — х₂х +  х₁ х₂ = = х (х — х₁) — х₂ (х — x₁) = (х — х₁) (х  — х₂).

Можна довести цю теорему і без теореми Вієта. 

Якщо х₁ і х₂ — корені тричлена х² + рх + q, то 

                                                                 х₁=  q ,   х₂=

Тому

                 (х — х₁) (х  — х₂)=(x+              q )(x+                  q )=(x + ^p )² - ( ^p2 - q)=

                                                                                                                                                                        2            4

= х² + рх + q

Отже, х² + рх + q =(х — х₁) (х  — х₂) .

Тричлен   ах² + bх + с розкладати   на   множники найкраще так, як це показано в підручнику.

Після вивчення цього матеріалу можна інакше розв'язувати і деякі з тих вправ, які раніше вже розв'язували. Наприклад, тепер учень до задачі «скласти квадратне рівняння, яке б мало корені 2 і 3» може зразу писати відповідь:

а (х — 2) (х — 3) = 0,

де а — довільне число, що не дорівнює нулю.

Пояснюючи цей матеріал, бажано також зауважити, що задачі «розкласти многочлен f(х) на множники» і «розв'язати рівняння f(x) = 0» дуже близькі. Якщо ми вміємо розв'язувати одну, то зразу ж можемо писати відповідь і для другої. Наприклад, коли знаємо, що рівняння х² -5х + 6 = 0 має корені 2 і 3, то многочлен, що є в його лівій частині, можна розкласти на множники, не задумуючись: х²—5х + 6 =  (х — 2) (х — 3).

І навпаки, якщо ми знаємо розклад многочлена х² + 3x - 4 = (x— 1)(x + 4),

то зразу можемо писати, що рівняння х² + 3х — 4 = 0 має такі корені: x₁ = 1, x₂ = — 4.

4. РІВНЯННЯ ТА СИСТЕМИ РІВНЯНЬ, ЩО ЗВОДЯТЬСЯ ДО КВАДРАТНИХ

У програмі є тема «Приклади рівнянь і систем, що зводяться до квадратних». Цю тему можна тлумачити по-різному. Адже є багато і логарифмічних, і тригонометричних та інших рівнянь, розв'язування яких зводиться до розв'язування квадратних рівнянь. Зрозуміло, що тут ідеться насамперед про дробові раціональні рівняння, що зводяться до квадратних, а також системи двох рівнянь, з яких одне першого, а друге — другого степеня.

Далі розглянемо такі рівняння і системи.

 

4.1  Дробові рівняння

З дробовими рівняннями, що зводяться до рівнянь першого степеня, учні вже мали справу. Тому тут немає потреби повідомляти щось нове з теорії. Бажано тільки повторити, що, розв'язуючи такі рівняння, обидві частини множимо на вираз, який містить невідоме. А від цього може утворитись рівняння, не рівносильне даному. Звичайно в даному випадку доводиться множити обидві частини на цілий алгебраїчний вираз, який має значення при всіх значеннях невідомого. Тому втрати коренів при цьому не буває. Але сторонні корені можуть появитися. Розв'язуючи такі рівняння, обов'язково треба робити перевірку. Тут перевірка є обов'язковою складовою частиною розв'язання.

                                                                                                              3x          ⁴

                Приклад 1. Розв'язати рівняння             =       + 1 

                                                                                                           2x 1     x 1

Р о з в ' я з а н н я. Зведемо рівняння до нормального вигляду: 

3х² +  3x =  8х - 4 + 2х² + 2х - х - 1, або  х²  - 6х + 5 = 0,

звідки

                                                  x1,2  = 6    36  20  3  2,           x1=5,          x1=1.

2

Перевірка. Підставимо знайдені корені 5 і 1 у дане рівняння:

1)        1  ;

2)      351  3 i         1 3 .

211

Обидва корені утвореного квадратного рівняння задовольняють і дане рівняння.

Відповідь: х₁ = 5, х₂ = 1. 

                Приклад 2. Розв'язати рівняння           ₂² + ^x₂ ^4 = ₂ ¹            

                                                                                                               x 4 x 2x              x 2x

Р о з в ' я з а н н я.

                                                                                       2                 x  4            1

                                                                                                                            ²                  

(x  2)(x  2) x(x  2) x  2x

2x + (x + 4)(x – 2) = x + 2,

2x + x² - 2x + 4x – 8 = x + 2, x² + 3x – 10 = 0,  х₁ = 2, х₂ = -5.

Перевірка. Перший корінь не задовольняє дане рівняння, бо при х = 2

                             2                ¹

вирази ₂ ⁱ  ₂ не мають ніяких значень. x 4 x 2x

Другий корінь х = -5 задовольняє рівняння, бо

                                                              2               (5)  4            1                1

                                                    ² +    ²     =        і        ²                      _                                                                               

                                                     (5)    4    (5)   2(5)       35     (5)    2(5)

Відповідь.  Рівняння має один корінь: х = — 5. 

Приклад 3. Розв'язати рівняння

                                                                                     x                2x                1

             . x3 (x1)(x3) x1

Розв'язання. Спільний знаменник: (х—1)(х — 3). 

Додаткові множники: х — 1, 1,  х — 3. х (х — 1) — 2х =  х — 3, х² — х — 2х = х — 3, х² —4 х + 3 = 0,

звідки х₁ = 1, х₂ = 3.

Перевірка. При х = 1 права частина даного рівняння не має значення; при х = 3 ліва частина рівняння не має значення.

Відповідь. Дане рівняння розв'язків не має.

На жаль, у шкільному збірнику немає жодної такої вправи, щоб обидва корені здобутого квадратного рівняння не задовольняли даного дробового. Тому вчителям варто скласти кілька таких вправ самостійно.

Можна скласти одне рівняння з параметром, а потім, підставляючи замість цього параметра різні числа, дістати багато рівнянь даного виду.

Наприклад,  рівняння     0  зводиться до  квадратного,

обидва  корені  якого не задовольняють дане дробове рівняння. Залишається його перетворити: 

x²  2x  ax  2a

  0, (x  2)(x  a)

(x²  ax)  (2x  4)  (2a  4)

  0, (x  2)(x  a)

                                                               x(x  a)             2(x  2)             2(a  2)

                                                                                                                                         0,

                                                         (x  2)(x  a)    (x  2)(x  a)    (x  2)(x  a)

звідки

                                                                                    x            2(a  2)            2

  . x  2 (x  2)(x  a) x  a

Підставляючи в це рівняння замість а числа 3, 4, 5, ..., дістанемо скільки завгодно однотипних рівнянь:

                                                                                     x                 2                 2

                                                                                                                              ,

x2 (x2)(x3) x3 x 4 2

  , x2 (x2)(x4) x4 x 6 2

  і т. д. x2 x_{2 }7x_10 x_5

Кожне з цих рівнянь не має жодного розв'язку, хоч приводить до квадратного рівняння, яке має дійсні розв'язки 2 і а.

Звичайно, не тільки такі дробові рівняння не мають жодного розв'язку. Може трапитись, що дане рівняння зводиться до такого квадратного, яке не має дійсних коренів. Наприклад, рівняння

                                                                                                     x             1

                                                                                                                         

2xc cx 2

зводиться до рівняння сх² + с = О, яке при с ≠ 0 не має дійсних розв'язків. Тому не має жодного розв'язку і кожне з таких рівнянь:

                                                                         x           1            x             1

                                                                                            ,                       0 і т.п

                                                                    2x 1    x  2    2x  3    3x  2

 

4.2. Системи рівнянь другого степеня У восьмирічній школі можна давати учням для рівнянь розв'язування тільки найпростіші системи рівнянь другого степеня з двома невідомими, що степеня зводяться до квадратних рівнянь. Спочатку бажано повторити, яке рівняння називають рівнянням другого степеня з двома невідомими.

Загальний вигляд рівняння другого степеня з двома невідомими х і у такий: ах² + bху + су² + dх +  еу + f = 0.

Тут коефіцієнти а, b, с, d, e, f — довільні числа, тільки а, b і с не можуть

одночасно дорівнювати нулю (бо інакше рівняння не було б рівнянням другого степеня).

Приклади рівнянь другого степеня з двома невідомими: х² + 3ху + 0,2у² — 5у = 0,

3z² — 2t² + t = 0, ху + 5 = 0.

Варто навести і контрприклади. Так, рівняння х² + 5ху² + 2 = 0 не є рівнянням другого степеня з двома невідомими, бо многочлен 5ху² не другого, а третього степеня.

Розв'язком одного рівняння з двома невідомими (будь-якого степеня) називають кожну пару значень невідомих, що задовольняють це рівняння.

Наприклад, рівняння 2х² — у = 0 має такі розв'язки: х₁ = 1, y₁ = 2; х₂ = 2, у₂ = 8; х₃ = 3, у₃ = 18 і т. д.

Якби для тих пар чисел, що задовольняють це рівняння, побудували на координатній площині точки з відповідними абсцисами і ординатами, то дістали б параболу, бо рівності 2х² — у = 0  і  у = 2х²  виражають одну  і ту саму  залежність.

Розглянуте вище рівняння має безліч розв'язків. Але не треба думати, що кожне рівняння другого степеня з двома невідомими має безліч розв'язків. Рівняння х² + (у — 1)² = 0 має тільки один розв'язок: х = 0, у = 1. Рівняння х²+ +3у² = -1 не має жодного розв'язку, бо квадрати — числа невід'ємні і їх сума не може дорівнювати -1.

Приблизно так можна пояснити учням рівняння другого степеня з двома невідомими. Потім бажано коротко сказати про розв'язування систем рівнянь, з яких одне першого степеня, а друге — другого. Розглянемо, як розв'язувати систему рівнянь виду  ах² + bху + су² + ах + еу +f= 0,  тх + пу + k = 0.

Такі системи можна розв'язувати способом підстановки. Треба в рівнянні першого степеня виразити одне невідоме через друге, наприклад у через х, і підставити це значення в рівняння другого степеня. В результаті дістанемо рівняння з одним невідомим х не вище як другого степеня. Розв'язавши його, знайдемо щонайбільше два значення х. Підставивши їх у рівняння першого степеня, дістанемо відповідні значення  невідомого у.

Така система рівнянь може мати не більш як два розв'язки (бо здобуте рівняння з одним невідомим не може мати більш як два розв'язки).

Спочатку бажано розглянути найпростіші приклади систем, до яких можна застосувати теорему, обернену до теореми Вієта. Потім слід поступово ускладнювати їх.

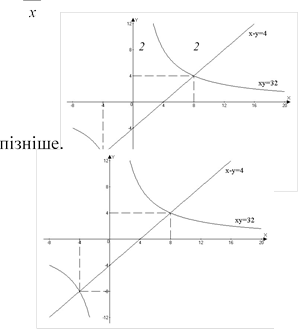
Приклад 1. Розв'язати систему

x  y  4,

                               

_xy  32.

Розв'язання. Перший спосіб. З другого рівняння маємо: у = ³² .

x Підставимо це значення в перше рівняння:

x - ³² = 4,  x² - 4x – 32 = 0,   x

x₁ =  - 4, x ₂ = 8_.

Тоді

y₁ = ³² = -8, y₂ = ³² = 4.

                                                                                            4                       8

Відповідь. Система має два розв'язки: х₁ = —4, у₁ = —8 і х₂ = 8, у₂ = 4.

Другий спосіб. Перепишемо дану систему так:

x  (y)  4,

                                      

_x (y)  32.

За теоремою, оберненою до теореми Вієта, маємо, що х і — у — корені рівняння z² – 4z – 32 = 0.

Розв'яжемо його. z₁ = -4, z₂ = 8. Отже, х₁ = z₁ = -4, у₁= -z₂ = -8, або х₂ = z₂ = 8, у₂ = -z₁ = 4.

Третій спосіб (графічний). Побудуємо в одній системі координат графіки рівнянь даної системи  (або, що те саме, графіки  функцій у = х -4 і y= ³² ). Абсциси і ординати точок перетину цих графіків  (мал. 6)  будуть: х₁=

= —4, у₁ =  —8; х = 8, у = 4. Це і є шукані два розв'язки даної системи.

Не обов'язково всі ці способи розглядати одночасно. Краще спочатку розв'язати кілька систем способом підстановки, а інші способи розглядати

 

 

 

 

 

 

                         Мал. 6                                                         Мал.7

 

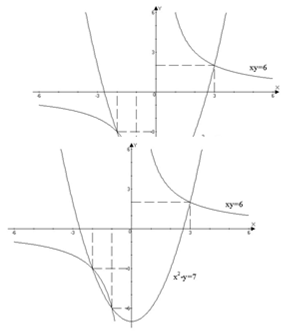
Систем рівнянь, з яких кожне — другого степеня, семикласникам давати не треба, бо ці системи зводяться до рівнянь третього і четвертого степенів, а їх семикласники розв'язувати не вміють. Хіба що в сильному класі можна запропонувати графічним способом розв'язати одну-дві таких системи, наприклад:

xy 6,

                  ₂                            

_x y 7.

Р о з в ' я з а н н я. Графіком першого рівняння є гіпербола. Графік другого рівняння — парабола. Справді, це рівняння можна подати у вигляді у = х² — 7, а графік такого рівняння, як відомо,— парабола, симетрична відносно осі ординат. Вітки її спрямовані вгору, а вершина знаходиться в точці (0; —7). Побудувавши графіки обох рівнянь (мал. 7), бачимо, що вони перетинаються в трьох точках:   (3; 2),  (—2; —3)   і  (— 1; —6).

Відповідь. Система рівнянь має три розв'язки: 

1)                x₁  = 3, у₂ = 2; 

2)                х₂ = -2, у₂ = -3;  3) х₃ = -1, у₃ = -6.

Перевірка показує, що це точні розв'язки.

 

5. ЗАДАЧІ НА СКЛАДАННЯ КВАДРАТНИХ РІВНЯНЬ

З методичного погляду розв'язування задач на складання квадратних рівнянь майже не відрізняється від розв'язування задач на складання лінійних рівнянь. В обох випадках учневі доводиться виконувати те саме: уважно вивчити задачу, вибрати невідоме, виразити через це невідоме кілька величин, про які говориться в задачі, скласти рівняння, розв'язати його і т. ін. Тому всі ті методичні зауваження, які звичайно даються до розв'язування задач на складання лінійних рівнянь, залишаються в силі і для задач на складання   квадратних   рівнянь.   Проте   деякі особливості   ці задачі всетаки мають. Звичайно задачі на складання квадратних рівнянь важчі (хоч і не завжди) від задач на складання лінійних рівнянь. Можна вказати й істотнішу відмінність. Усі задачі на складання лінійних рівнянь можна розв'язати арифметичними методами, всі вони — типові арифметичні задачі. А задачі, які зводяться до квадратних рівнянь, за небагатьма винятками, розв'язувати   арифметичними   методами   не   можна.

При розв'язуванні задач, що зводяться до квадратних рівнянь, більше уваги доводиться приділяти дослідженню розв'язку. Навіть якщо задача і не містить буквених даних, все одно доводиться робити деяке дослідження — з'ясовувати, який з двох коренів квадратного рівняння задовольняє задачу. При цьому часто треба виходити за межі математики, досліджувати, чи може трапитися та чи інша ситуація в житті, чи ні.

Розглянемо задачу :

«Тепловоз, пройшовши перший перегін 24 км, був затриманий деякий час, а тому наступний перегін проходив з швидкістю, більшою, ніж попередня, на 4 км за годину. Незважаючи на те, що другий перегін був довший від першого на 15 км, тепловоз пройшов його за час, тільки на 20 хв більший, ніж потрібно було на проходження першого перегону. Визначити початкову швидкість тепловоза».

Розв'язання. Позначимо початкову швидкість тепловоза

буквою v. Тоді перший перегін він пройшов за ²⁴ год. Другий перегін  v

завдовжки  24  км + 15  км = 39 км  тепловоз пройшов з швидкістю (v + 4)

км/год, тому затратив на це  ³⁹  год. v  4

У задачі відомо, що другий перегін тепловоз проходив на  год довше,

ніж перший. Отже,

                                                                                                39        24       1

 -  = , v  4 v 3

звідки v² - 41v + 288 = 0, v₁ = 9, v₂ =32.

Як бачимо, складене за умовою задачі рівняння має два корені. Деякі учні вважають, що задача має два розв'язки. Інші перший корінь відкидають, пояснюючи, що тепер тепловози не їздять з такою малою швидкістю. Перші не погоджуються: тепловоз може йти з швидкістю 9 км/год, якщо машиніст має якесь спеціальне завдання, наприклад перевірити, чи не пошкоджені рейки, або якщо цей тепловоз несправний, і т. д.

Звичайно, на уроці корисно хвилину-дві поговорити на таку тему, але пропонувати таку задачу на контрольну роботу не варто. .     

5.1. Способи розв’язування задач

Переважну більшість задач на складання квадратних рівнянь, які розв'язуються в школі, можна розв'язати кількома способами. Для прикладу розглянемо задачу.

«Колгосп   мав засіяти  200  га  до  певного  строку,   але  він засівав щодня на 5 га більше, ніж було передбачено планом, і тому закінчив сівбу на

2 дні раніше строку. За скільки днів колгосп закінчив сівбу?» Розв'язання.

 Перший спосіб. Нехай сівба тривала х днів; тоді за планом вона мала тривати (х + 2) дні; колгосп засівав щодня по  ²⁰⁰ га; мав засівати щодня по x

200  га.

x  2

У задачі сказано, що колгосп засівав щодня на 5 га більше, ніж передбачалось планом, тому ²⁰⁰ більше від  ²⁰⁰   на 5. Маємо рівняння:

                                                                                  x                             x 2

                                                                                             200       200

 -  = 5, x x  2

звідки х² + 2х — 80 = 0, х₁ = — 10,   х₂ = 8.

Від'ємне значення   х   задачу не   задовольняє, тому х = 8.

 Відповідь.  Колгосп закінчив сівбу за 8 днів. 

Другий спосіб. Нехай  колгосп засівав щодня по х га; мав засівати по (х

— 5)  га; сівба тривала всього  ²⁰⁰ днів; мала тривати ²⁰⁰ днів. x  x  5

У задачі відомо, що колгосп закінчив сівбу на 2 дні раніше строку, тому 

200                            200

 менше від    на 2. Отже, x      x  5

                                                                                              200       200

 -  = 2, x 5 x

звідки

х²— 5х — 500 = 0,

х₁ = — 20,   х₂ = 25.

Від'ємне значення х задачу не може задовольняти, тому його відкидаємо. Залишається х = 25. По стільки гектарів засівали в колгоспі щодня. Але всього засіяли 200 га, отже, сівба тривала 200 : 25 = 8 (днів).

Третій спосіб. Нехай сівба тривала х днів. Оскільки колгосп щодня засівав на 5 га більше, то за х днів він засіяв на 5 х більше, ніж мав засіяти за х днів. Виходить, 5х га він мав засіяти за 2 дні. Тоді за день він мав сіяти по

5          200  х га. З другого боку, він за день мав засівати по  га.  

2                                                                                                    x  2

Отже,

                                                                                                  5            200

 х =  

                                                                                                  2           x  2

або x² + 2х — 80 = 0, x₁ = —10,   х₂ = 8.

Задачу задовольняє другий корінь: 8 днів. 

Четвертий спосіб. Припустимо, що колгосп сіяв усього х днів по у га щодня, мав сіяти (x + 2) днів по (у — 5) га щодня. Він засіяв і мав засіяти всього 200 га. Тому  ху = 200, 

(х + 2)(у — 5) = 200, звідки дістаємо однe рівняння з невідомим х: 

(x + 2) ( ²⁰⁰ -5) =200, x

х² + 2х — 80 = 0, x₁= —10,  x₂ = 8.

Відповідь. 8 днів.

Ми розглянули чотири досить відмінні один від одного способи. Взагалі є понад десять різних способів розв'язування цієї задачі. Те саме можна сказати і про більшість інших задач, що їх розв'язують учні на уроках алгебри.

Зрозуміло, не треба щоразу вимагати, щоб учні одну й ту саму задачу розв'язували кількома способами. Але іноді корисно проаналізувати кілька способів. Тоді учні глибше проникають у зміст не тільки цієї задачі, а й взагалі задач даного типу.

5.2. Задачі з буквеними даними

Вище  ми розглядали задачі на  складання  рівнянь, в умовах яких давалися конкретні числові значення величин. Але в VII—VIII класах, крім даними таких задач, доводиться розв'язувати також задачі з буквеними даними. Розв'язують ці задачі так само, тільки, зрозуміло, у відповідях дістають не числа, а деякі вирази, що залежать від даних у задачі букв. Це особливих труднощів для учнів є становить. Значно гірше справа стоїть з дослідженнями, які тут бувають досить складні.

Раніше в методичній літературі багато писали про дослідження таких задач. У дослідженнях пропонувалось показати, як змінюватиметься розв'язок задачі, якщо змінювати значення букв, і т. ін. Тепер таких досліджень у восьмирічній школі не роблять. Домовились вважати, що дослідити розв'язок задачі з буквеними даними — це означає з'ясувати, при яких системах значень цих букв задача має розв'язки і скільки.

Проілюструємо сказане на двох задачах.

Задача 1. Куплено m яблунь, щоб посадити на кожну ділянку порівну. Але ділянок виявилось на 2 більше, тому на кожну з них довелося посадити на 3 яблуні менше, ніж передбачалося. Скільки було ділянок?

Розв'язання. Позначимо кількість ділянок буквою х. З умови задачі випливає рівняння

                                                                                                    m       m

  3. x  2 x

Корені його такі:

                                                                x1 = 3 9 6m ,               x2 = 3 9 6m

                                                                                     3                                             3

Проведемо дослідження. Число m за умовою задачі додатне, тому  

9  6m  3 і, значить, другий корінь від'ємний. Отже

                                                                                           x = 3     9  6m .

3

Залишається визначити, яких значень може набувати в здобутій формулі буква m.  Число х повинно бути натуральним і більшим від 2. Тому 96m повинно бути цілим, кратним 3 і більшим від 3. А це можливе тільки тоді, коли 9 + 6m = 9k², де к — ціле, більше від 1, звідки 6m=9(k² — 1),

m =  (k² — 1).

Відповідь. Ділянок було (3+ 96m ), де m =  (k² — 1) і k —

натуральне число, більше від 1.

Іноді в дослідженні не тільки доводиться уточняти, які значення задовольняють задачу, а й з'ясовувати, чи всі випадки охоплено складеним рівнянням, чи не допущено втрати розв'язків. Це найчастіше буває при розв'язуванні задач геометричного змісту. Розв'яжемо одну з таких задач.

Задача 2. Знайти сторони рівнобедреного трикутника, якщо відомо, що дві нерівні висоти його дорівнюють а і b.

Розв’язання. Позначимо сторони трикутника (мал. 8, а) буквами: АС = АВ = х, СВ = у. Тоді, користуючись теоремою Піфагора і формулою для обчислення площі трикутника, можна скласти таку систему:

x₂  y4² a2, bxay.

Визначивши   з другого   рівняння   у  і   підставивши  його  в перше, дістанемо:

                                                                                                2             b2           2              2

x               ₂ x  a ,

4a

2a² x.

4a² b²

Тоді

y       = ^b x = ^2ab a 4a2 b2

Отже,

                                                                                        2a²                                                             2ab

                                                                                      x,              y =

                                                                                      4a² b²                                                4a² b²

 

Тому, діставши цю відповідь, учні вважають, що вони закінчили розв'язання. Проте обмежуватись цим не можна. A

 

 

                                            H

 

 

 

                                                               B                                          D            B

                                              а                                            б

 

Мал. 8

 

Бажано звернути увагу, що в здобутих значеннях х і у під радикалом маємо різницю 4а² — b². Ця різниця повинна бути додатною, а це можливе тільки при b < 2а.

Отже, даний вище розв'явок задачі правильний не при будь-яких додатних а і b, а тільки при b < 2а.

Але це ще не все. Ми розглянули тільки один випадок, коли на основу у опущено висоту а. Але для тих самих а і b можливий інший випадок (мал.

8,б). Тоді маємо: 

                     2 y2                     2

x  4  b ,

ax  by.

Звідки

                                                                                                2            a2          ₂              2

                                                                                              x    ₂ x  b ,

4b

                                                                                             2b²                                                2ab

x, y = 

                                                                                          4b² a²                                    4b² a²

У цьому випадку а < 2b.

Відповідь.    Якщо а < 2b < 4а, то задача  має два  розв'язки:

1)    x₁  ^2a2              , y₁ =;

2)    x_{2 } , y₂ =     .

Якщо b ≥  2а, то задача має один розв'язок:

                                                                             x       2b2               , y =      2ab       .

                                                                                         4b² a²                                    4b² a²

 Якщо а ≥ 2b, то задача також має один розв'язок:

                                                                                          2a^{2                                                         2ab}

                                                                                      x _,                     y =.

                                                                                       4a² b²                                             4a² b²

                                                                                6.     ВИСНОВОК

Тема «Квадратні рівняння» - найважливіша і найцікавіша тема з усіх розділів математики. Основною метою вивчення даної теми є ознайомлення учнів з поняттям «квадрктне рівняння» та його видами; формування навичок розвязування квадратних рівнянь та рівнянь,що зводяться до квадратних за допомогою формул коренів та теореми Вієта.

Під час вивчення важливо показати значимість цієї теми – широке застосування рівнянь в найрізноманітніших галузях застосування математики. Вчитель повинен зацікавити учнів, використовувати різні методи, форми та прийоми проведення уроків.

7. СПИСОК ВИКОРИСТАНОЇ ЛІТЕРАТУРИ

1.Кочетков Є.С., Кочеткова К.С., Алгебра і елементарні функції, ч.ІІ, - К.: «Радянська школа», 1969.

2.      Туманов С.И., Алгебра, М., «Просвещение» 1966.

3.      Барсуков О. М., Алгебра, Підруник для 6-8 класів, К., «Радянська школа», 1970.

4.Бевз Г.П., Методика викладання алгебри. Посібник для вчителів, - К.: «Радянська школа», 1971.

5.                  Репьев В.В., Методика преподавания алгебрі в восьмилетней школе,

М., «Просвещение», 1967.

6.                  Барыбин     К.      С.,     Методика   преподавания       алгебры,     М.,

«Просвещение», 1965.

7.                  Лоповок Л.М., З досвіду викладання математики в середній школі, - К.: «Радянська школа», 1957.

8.                  Методика преподавания математики в средней школе:Частная методика /Сост. В.И. Мишин, - М.: Просвещение, 1987.

9.                  Бевз Г.П., Алгебра: Проб. підруч. для 7-9 кл. серед. шк. – К.: Освіта, 1996.

10.             Возняк Г.М., Маланюк М.П., Взаємозв’язок теорії з практикою в процесі вивчення математики: Посібник для вчителя. – К.: «Радянська школа», 1989.

11.             Кучевський М. І., Квадратні рівняння., //Математика в школах України//. 2007., ст 34-38.

12.             Попко О. Ю.,Квадратні рівняння, //Математика в школах

України//. 2007., ст 24-25.