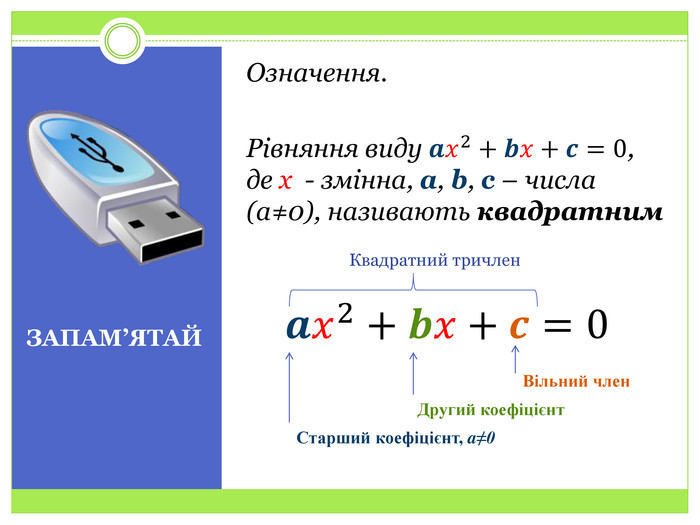
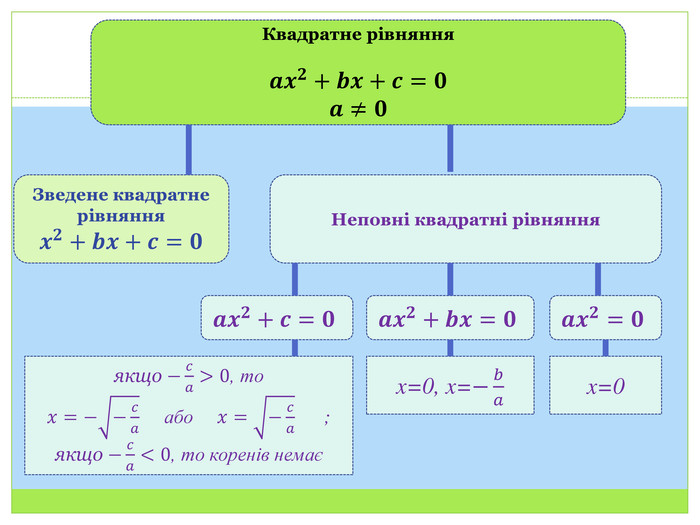
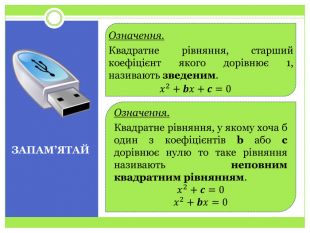
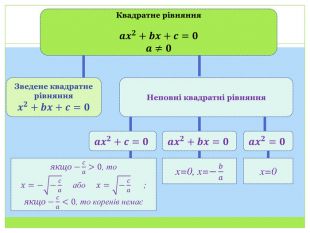
Квадратні рівняння. Неповні квадратні рівняння
Про матеріал
Презентація до уроку алгебри у 8 класі на тему "Квадратні рівняння. Неповні квадратні рівняння". Формування поняття квадратного рівняння, неповного квадратного рівняння Перегляд файлу
Зміст слайдів


Безкоштовний сертифікат
про публікацію авторської розробки
про публікацію авторської розробки
Щоб отримати, додайте розробку
Додати розробку