КВАДРАТНІ   РІВНЯННЯ   З  ПАРАМЕТРОМ

   Майже вся теорія квадратного тричлена, а також розв’язання багатьох задач, пов’язаних з ним, базується на прийомі, що називається «виділенням повного квадрата». Застосовуючи цей прийом до квадратного тричлена  , приходимо до рівності:

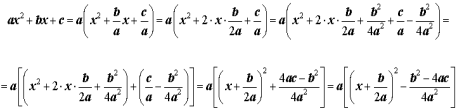
 Вираз  D= b² - 4ас  називають дискримінантом.

Квадратне рівняння може мати два корені (D>0), один корінь (D=0) або не мати коренів (D<0). Корені квадратного рівняння  х₁ і х₂ дорівнюють:

;

.

 Правда, нумерація коренів умовна. Зазвичай намагаються занумерувати їх у порядку зростання, але це не обов’язково. Також деякі термінологічні проблеми виникають у випадку D=0, тож зауважимо, що вирази  «квадратне рівняння має один розв’язок» і «квадратне рівняння з рівними коренями» означають одне і те ж.

 Якщо другий коефіцієнт квадратного рівняння  - парне число, тобто b = 2k,

то при розв’язуванні квадратного рівняння можна користуватися формулою: , де , .

 До азбуки квадратного тричлена відноситься також і теорема Вієта. Для того, щоб х₁ і х₂  рівняння  ах² + bх + с = 0 , необхідно і достатньо, щоб виконувались рівності:

             

.

      Звернемо увагу на те, що тут сформульовано два твердження – пряме та обернене. Часто обмежуються одним прямим твердженням.

 Зауваження. Важливо звертати увагу учнів на випадки, коли коефіцієнт при х²  дорівнює нулю, і розглядати їх у першу чергу, що допоможе учням уникати поширеної помилки: взагалі не розглядати таких випадків.

 

Рівняння з вимогою

«розв’язати для всіх значень  параметра»

 

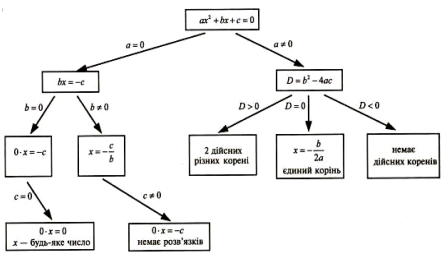
 Розв’язання рівнянь такого типу слід з питання «А чи є воно квадратним?». Далі можна скористатись схемою.

 

Приклад 1. Розв’язати рівняння    ax² – 2x + 4 = 0.

Розв’язання

Якщо a = 0, то x = 2.  

Якщо  а ≠ 0, то рівняння є квадратним.

D = 4 – 16a.

Якщо  D < 0, тобто a >0,25, рівняння розв’язків не має.

Якщо D = 0, тобто a = 0,25,  то x = 4.

Якщо  D > 0, тобто a < 0,25 , то рівняння має два кореня

x_1,2 = .

Приклад 2.  Розв’язати рівняння  x² 2x a 0.

Розв’язання

Рівняння квадратне, тому розв’язки залежатимуть від дискримінанта:

D 1a .

Якщо  а > 1, то D 0,  то коренів немає.

Якщо  а = 1, то D 0, то отримаємо один корінь  х = 1.

Якщо  а < 1, то D 0 , то рівняння має два різних дійсних кореня   x_1,2 11a .

Відповідь. Якщо  а > 1, то розв’язків немає;

Якщо  а = 1, то  х = 1; якщо а < 1, то  x_1,2 11a .

 

Приклад 3.  Розв’язати рівняння: (+1)х²+2х+ −2=0.

Розв’язання

1) Якщо +1= 0 тобто = -1, то задане рівняння буде мати вигляд:     -2х – 3 = 0, тобто х =-

2) Якщо +1≠0 ( ≠ -1), то одержимо квадратне рівняння, дискримінант якого D=4(+2). Тому розглянемо три випадки:

1. якщо D=0, тобто 4(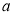+2) = 0, то 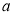= -2 i х = -2;
2. якщо D<0, тобто 4(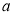+2) < 0 ( 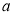< -2), то коренів немає;
3.  якщо D>0: 4(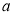+2) > 0; 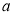> -2 і 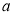≠ -1, тобто   -2 <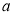< -1  і 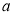> -1, то квадратне рівняння має два різні корені:

х₁=;      х₂=.

Відповідь.  Якщо =-1, то х=-; якщо ≠-1 і ≥-2, то х=.

   

Приклад 4. Розв’язати рівняння 3(2а – 1)х² – 2(а + 1)х + 1 = 0 .

Розв’язання

Якщо а = ,  дане рівняння перетворюється в лінійне рівняння:

0·х² – 2( + 1)х + 1 = 0;

−3х + 1 = 0;

 х = .

Якщо а ≠ , то дане рівняння є квадратним. Знайдемо дискримінант:

= (а + 1)² – 3(2а + 1) = а² + 2а +1 – 6а +3 = а² −4а +4 =

= (а – 2)² ≥ 0 .

= 0, якщо а = 2. Тоді рівняння набирає вигляду:

9х² – 6х + 1 = 0;          (3х – 1)² = 0;          х = .

> 0, якщо а ≠ 2. Тоді рівняння  два корені:

х₁ =      і        х₂ = .

Відповідь. Якщо а = , а = 2,   то  х = ;

 якщо  а ≠ ,    а ≠ 2,    то  х₁ = ,   х₂ = .

 

Приклад 5.  Розв’язати рівняння

  .

Розв’язання

Якщо а = 2,  дане рівняння перетворюється в лінійне,  .

Якщо а ≠ 2, то дане рівняння – квадратне.

D =

      Розв’язуючи нерівність , знаходимо ті значення а, за яких набувають дійсних значень:  \,   то
 

Відповідь. Якщо а = 2,   то  х =;

якщо

 

Приклад 6.   Розв’язати рівняння .

Розв’язання

 Перенесемо всі доданки із правої частини рівняння в ліву з протилежним знаком і зведемо  коефіцієнти при однакових степенях х:

.

Застосуємо формулу перетворення різниці квадратів у добуток і винесемо спільний множник  (а+1) за дужки : .

 Якщо параметр то рівняння зводиться до тотожності 0=0. Отже, його розв’язками є всі дійсні числа. Нехай , тоді  .Поділивши обидві частини рівняння на (а+1), отримаємо . В залежності від значень параметра а одержимо рівняння різного виду.

 Якщо а=1, то рівняння стає лінійним. Якщо , то рівняння буде квадратним.

 Обчислимо дискримінант рівняння:

.

0  при .  Тоді х₁ = х₂ = = 2.

0  при .  Тоді х_1,2 =

Відповідь. Якщо а = −1,   то  х

Якщо а = 1,   то  х = 1.

Якщо ,  то   х₁ = х₂ = 2.

Якщо то  х_1,2 =

Якщо ,  то рівняння розв’язків не має.

 

 

Існування коренів  (коренів певних знаків)

 

 Розглянемо завдання на співвідношення між коренями квадратного рівняння з параметрами. Їх можна розв’язувати користуючись схемою. Але деколи зручніше не виписувати значення коренів через дискримінант, а використовуючи теорему Вієта.

Рівняння має два додатні корені
Рівняння має два від’ємні корені
Рівняння має корені різних знаків
Рівняння має два різні додатні
Рівняння має два різні від’ємні корені

 

Приклад 7.   Знайдіть всі значення параметра  а, при яких рівнянння 3x² 2(a 3)x a² 2a 0 має корені різних знаків.

Розв’язання

Якщо  корені x₁ і x₂ – корені рівняння, то x₁ · x₂ 0 .

За теоремою Вієта маємо: < 0, звідки        

Відповідь.  (− – 2)   (0; +.

 

Приклад 8.   Довести, що при будь-якому значенні а рівняння має розв’язок.

Розв’язання

  Можна, звичайно, спробувати знайти дискримінант і довести, що він додатний. Але не будемо поспішати. Позначимо ліву частину даного рівняння як f(x). Відразу зрозуміло, що при будь-якому значенні  а. Твердження задачі буде доведено, якщо ми знайдемо х₁, для якого . Спробуємо . (Вибір такого значення є зрозумілим,  оскільки у цьому випадку зникають члени з ) при будь-якому значенні а. Тепер легко можна зробити висновок, що рівняння завжди матиме розв’язок. Більше того, якщо , тобто і , дане рівняння матиме два корені; при цьому завжди є корінь, який задовольняє нерівність  .

Приклад 9.   Знайти значення параметра а, при якому  рівняння має лише один корінь.

Розв’язання

 

     Якщо  а = 2, то рівняння – лінійне  (4 − 4)∙х + 3 = 0, що немає коренів.

     Якщо а ≠ 2, то рівняння квадратне і має один корінь лише тоді, коли D = 0.

.

D = 0 при а₁ = 2 и a₂ = 5.  Значення  а = 2 не задовольняє умову задачі.

Відповідь.  а = 5.

Рівняння з умовами щодо  коренів

 

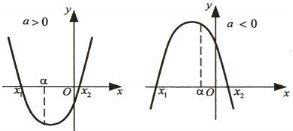
Нехай і – корені рівняння  = 0,

де; , , ; – абсциса вершини параболи    .

Тоді мають місце такі твердження:

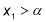•    , якщо виконуються умови: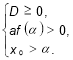  
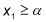•    , якщо виконуються умови: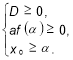   

 

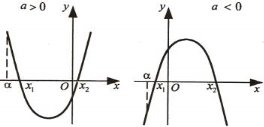
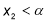• , якщо виконуються умови: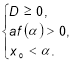  
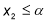• , якщо виконуються умови: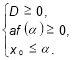   

 

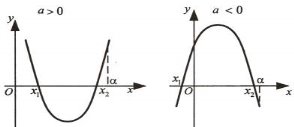
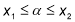• , якщо виконуються умова .

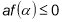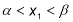• , якщо виконуються умови: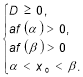  

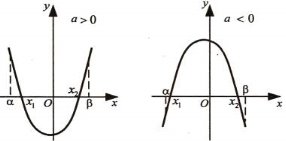
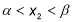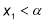• , ,  якщо виконуються умови: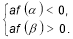  

 

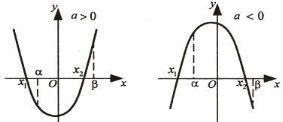
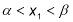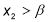• , ,  якщо виконуються умови:  

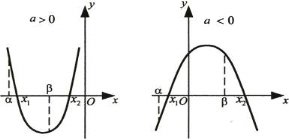
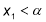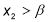• , ,  якщо виконуються умови: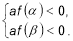  

 

 

 

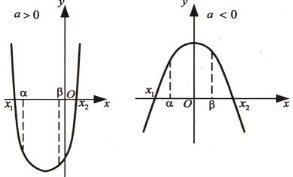
Приклад 10.  При яких значеннях а один з коренів рівняння

дорівнює квадрату іншого?

Розв’язання

 Для визначення шуканих значень а складемо систему, в якій два перші рівняння описують теорему Вієта для даного квадратного рівняння , , а третє співвідношення містить умову, яка накладається на його корені:.

У даному випадку для визначення та зручно вибрати друге і третє рівняння системи:

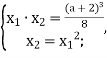  тобто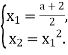

Підставляючи знайдені вирази в перше рівняння системи, одержимо:    ,  ,

Відповідь. а= −1,     або    а=3.

 

Приклад 11.  При яких значеннях параметра а корені рівняння

більші 1?                                                

Розв’язання

Очевидно, що задача рівносильна наступній: при яких значеннях параметра а корені квадратного тричлена

  більші 1.

 Перехід від одного формулювання задачі до іншого, підкреслює загальну ідею, що пов’язана з описом тих чи інших властивостей квадратного тричлена в їх геометричній інтерпретації на графіку.

Для того, щоб корені квадратного тричлена були більші числа , необхідно і достатньо виконання умов:

     

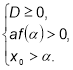
 При а=0 рівняння має корінь х = −1,  який не задовольняє умову задачі.

Розглянемо випадок . При таких а умови запишуться у вигляді    .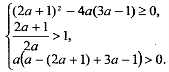

Розв’язуючи цю систему, знаходимо, що  . Очевидно, що цей же результат ми отримали б і розв’язуючи  нерівність  ,   де − менший корінь рівняння.

Відповідь. .

 

Приклад 12.  При яких значеннях параметра а один із коренів рівняння  тричлена (а² − + (а² + а – 1) – а³ + а = 0   більший,  ніж число а, а другий менший а?

Розв’язання

 Задача рівносильна наступній: при яких значеннях параметра а корені квадратного тричлена  у(х) = (а² − + (а² + а – 1) – а³ + а = 0   лежать на дійсній осі по різні сторони від точки х = а?

 Для розв’язування цієї задачі скористаємося тим загальним фактом, що для того щоб корені квадратного тричлена  лежали на дійсній осі по різні сторони від числа , необхідно і достатньо виконання умови  .

 

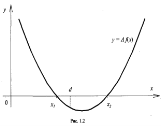
 У нашому випадку ця умова набуває  вигляду (а² − < 0.

Тобто, вимогу задачі задовольняють розв’язки нерівності

(а² −( а² −2) а² + (а²− а −1)а – а³ + а) < 0, де   (а² − ≠ 0

 (а = ± не задовольняють умову задачі).

 Розв’язуючи отриману нерівність, знаходимо, що а

Варто сказати, що розв’язувати  цю задачу іншим способом, розглядаючи нерівності   і  ,  досить складно.

Відповідь. а

 

Приклад 13.  При яких значеннях параметра а корені   та рівняння (3а + + (а – 1) + 4а +3 = 0 задовольняють умовам       < − 1  <  < 1?      

Розв’язання

 Задача рівносильна наступній: при яких значеннях параметра а тільки один, а саме – більший корінь квадратного тричлена

f(x) = (3а + + (а – 1+ 4а +3 , де 3а + належить інтервалу  (-1; 1), а другий – менший   -1.

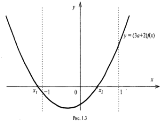
Вимоги в даній задачі виконуються тільки з-за умов:

.

Таким чином ми приходимо до системи:

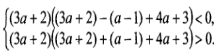
Розв’язуючи цю систему, приходимо до висновку, що

а.

Відповідь.   а

 

Приклад 14.  При яких значеннях параметра а корені рівняння = 0 мають різні знаки і обидва по модулю менші 4?

Розв’язання

 

 Нехай . Тоді вимоги задачі виконуються, якщо сумісна система

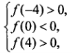, яку запишемо у вигляді 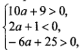і якій задовольняють всі а.

Відповідь.  а

 

Приклад 15.  При яких значеннях параметра а квадратний тричлен  (k – 1)х²  + (k + 4)х +  k + 7  можна представити у вигляді повного квадрата?

 

 

Розвязання

    Квадратний тричлен  ax² + bx + c можна представити у вигляді   a(х –x₀ )², якщо його корені рівні  х₁ = х₂ = x₀ . Тобто коли D = 0.  В даному випадку D  = (k +4)² −4(k − 1)( k + 7) = 0.

Розв’язавши  останнє рівняння,  отримуємо k = - і k = 2.

Відповідь.   k = - і k = 2.

 

Приклад 16.  Знайти всі значення параметра , при кожному з яких корені рівняння належать інтервалу .

Розв’язання

 Нехай .  ,

Якщо , то .

Якщо , то задача рівносильна виконанню умов:

 

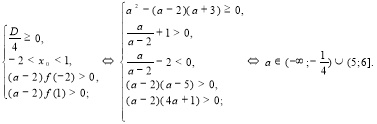Відповідь.   .

Приклад 17.  Знайти всі значення параметра , при кожному з яких лише один корінь рівняння належать інтервалу .

Розв’язання

Рівняння квадратне.

9.

Корені х = а – 1  і  х = а + 2.

1< а  − 1 < 5,

2< а  < 6.

1< а  + 2 < 5,

−1 < а  < 3.

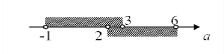
Бачимо, що рівно один корінь належить інтервалу при −1 < а  ≤2   або   3 ≤ а  < 6.

Відповідь: .

 

Приклад 18.  Знайти всі значення параметра , при кожному з яких корені рівняння   має корені різних знаків і модуль додатного кореня більший, ніж модуль від’ємного.

Розв’язання

 Корені цього квадратного рівняння задовольняє умову тоді і тільки тоді, коли їх добуток буде від’ємним числом, а сума – додатним. За теоремою Вієта отримаємо систему:

Відповідь. .

Приклад 19.  Знайти всі значення параметра , при кожному з яких корені рівняння   більші 3.

Розв’язання

 І спосіб. D 2a 2 ; x₁ 3a  , x₂ 3a  .

Щоб корені були більші 3 ( 3 ≤ x₁ ≤x₂), досить розв’язати тільки одну нерівність: 3a −3,   відокремивши радикал, отримаємо нерівність 3a 3,  яка рівносильна системі:

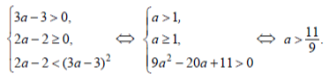
ІІ спосіб. Розглянемо функцію: f (x) x² 2ax 9a² 2a 2.

Її корені більші 3, якщо виконується система:

 

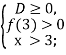
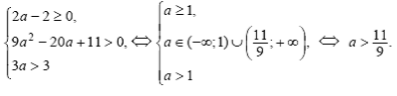
Відповідь. .

Взаємне  розташування коренів двох квадратних рівнянь

     З’ясуємо питання про взаємне розташування коренів двох квадратних рівнянь.

      Нехай рівняння має корені , а рівняння   має корені  , при чому  . У цьому випадку кажуть, що корені рівняння перемежовуються.

      На рисунку  показане взаємне розташування графіків цих функцій. Графіки мають єдину точку перетину з абсцисою .

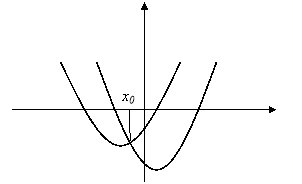                                            Очевидно, що , звідки  . (Відмітимо, що при   графіки співпадають або не перетинаються.) Нехай  , тоді  , або , звідки 

.                (*)                                  

 

  Приклад 20. При яких значеннях параметра корені рівнянь  та  перемежовуються ?

Розв’язання

У даному випадку

З нерівності (*) одержуємо, що

 ,

або звідки

Відповідь. 

 

Приклад 21.   Знайти всі значення параметра , при кожному з яких рівняння  (1 – 2а)х² – 6ах – 1 = 0 і  ах² – х + 1 = 0 мають хоча б один спільний корінь.

Розв’язання

 

При а ≠ 0 и 1 – 2а ≠ 0 запишемо умову (*) для цих рівнянь:

( + )²  = (− + ) (− − ).

Спростивши рівняння, отримаємо:

 (1− а)² = -  (6а² + 2а – 1)( 6а + 1). Розкриємо дужки та перенесемо всі доданки в одну частину, винесемо а за дужки:

а( 36а² + 19а – 6) = 0.

 За умовою  а ≠ 0, тому тільки

36а²+ 19а – 6 = 0,

 а₁ =   і а₂ =   .

Підставимо значення а в друге рівняння ах² – х + 1 = 0.

Отримаємо

   х² – х + 1 = 0,  D отже  а =  не задовольняє умову.

х² – х + 1 = 0.   D ≠ 0.

Відповідь.   а = .

 

Рівняння, що містять модуль

 

Приклад 22.  При якому значенні параметра р  рівняння

 | х² – 5х + 6 | + | х² – 5х + 4 | = р  має рівно чотири корені?

Розв’язання

 

Розглянемо функцію   у = | х² – 5х + 6 | + | х² – 5х + 4 |

Так як х² – 5х + 6 = (х – 2)(х – 3)  і  х² – 5х + 4 = (х – 1)(х – 4), то

 y = | (х – 2)(х – 3) | + | (х – 1)(х – 4) |.

Розв’яжемо рівняння на кожному із п’яти проміжків, на які розбивають числову вісь корені квадратних тричленів:

1. x < 1

y = x² – 5x + 6 + x² – 5x + 4,

y = 2x² – 10x + 10,

y = x² – 5x + 5  − парабола.

2. 1 < x < 2

y  = x² – 5x + 6 –  x² + 5x – 4,

y = 2 – пряма.

3. 2 < x < 3

y = – x² + 5x – 6 –  x² + 5x – 4,

y = – 2x² + 10x – 10,

y = – x² + 5x – 5 – парабола.

4. 3 < x < 4

y = x² – 5x + 6 – x² + 5x – 4,

y = 2 – пряма.

5. x > 4

y= x² – 5x + 6 + x² –5x + 4,

y = x² – 5x + 5 – парабола.

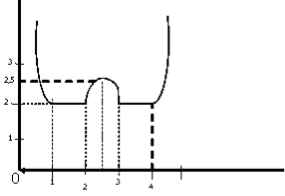
Побудувавши на кожному із проміжків відповідні графіки, отримаємо:

х

Отже, рівняння має чотири корені за умови    2 < а < 2,5.

Відповідь. а .

 

Приклад 23. При якому найбільшому цілому значенні параметра рівняння   має рівно чотири корені?

Розв’язання

Початкове рівняння матиме 4 корені, якщо рівняння матиме корені, і обидва вони будуть додатними. рівняння матиме корені за умови , звідки .

За теоремою Вієта      ,  .

Отже, для того щоб обидва корені були додатними, необхідно щоб було додатним.

Маємо: , тому найбільшим цілим значенням буде 6.

Відповідь. 6.

 

 

Приклад 24.  Знайдіть усі значення параметра а, при яких рівняння  2х² + (2а–10)|x| +a² – 10 a +16 = 0 має два розв'язки.

Розв'язання

 Перша ідея – виділити повний квадрат відносно параметра а:

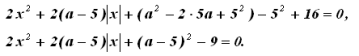
Наступна ідея не настільки очевидна, але абсолютно типова – виділити повний квадрат щодо модуля х. Тоді не буде необхідності в розкритті модульних дужок.

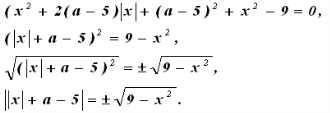
 Першу частину розв'язання виконано. Ми прийшли до того, що ліва частина рівняння залежить від параметра, а права не залежить. Далі має бути  дослідження кількості точок перетину графіків рівнянь:

Перетворимо друге рівняння:

Друге рівняння описує коло із центром на початку координат і радіусом рівним 3. Це коло не залежить від параметра й не змінює свого положення в процесі дослідження. Більш цікавим  є графік першого рівняння, точніше  множина графіків. Параметр а надає цьому рівнянню динамічність переміщення щодо координатних осей і зміну форми графіка від прямого кута до ламаної лінії із прямими кутами. А саме, при  а – 5 ≥ 0  графік першого рівняння має вигляд:

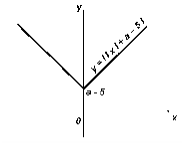
При  а – 5 < 0  графік перетвориться на ламану лінію:

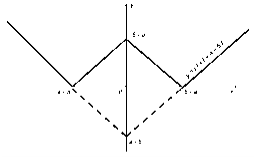
Досліджуємо графічно розв'язок системи: 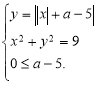Тоді система й вихідне рівняння мають два розв'язки.

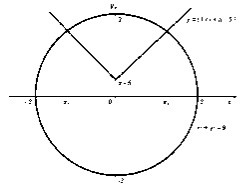
Тепер досліджуємо цю же систему при  a – 5 < 0. У цьому випадку два розв'язки можливі коли: -3 < a – 5 < 0, тобто для значень параметра в межах 2 < a < 5.

Графічно ці розв'язки отримуються у такий спосіб:

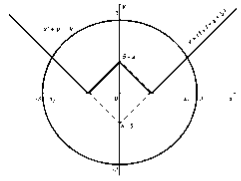
При a – 5 = −3 тобто при a = 2 рівняння має три корені.      При    a < 2 рівняння має чотири розв'язки доти, доки графіки кола й ламаної мають чотири спільні точки. Але настане момент, коли відповідні січні стануть дотичними, і тоді рівняння знову буде мати тільки два розв'язки:

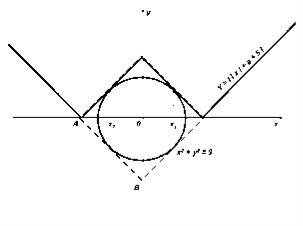
У  цьому випадку: АВ = 6,  ОВ = 3,  В(0;- 3),  а - 5 = -3√2,

 а = 5 - 3. Поєднуючи всі отримані розв'язки, маємо:

a (2;8,)  a =5 – 3.

Відповідь.  a (2;8),  a =5 – 3.

 

Приклад 25.  Вказати всі значення параметра а , при яких рівняння   ׀х² +3ах= −3а  має лише два розв’язки.

Розв’язання

 Перш за все відмітимо, що рівняння  ׀х² +3ах= −3а  може мати розв’язки тільки при а < 0 (а Графік y₁= ׀х² +3ах  отримаємо з параболи y = х² +3ах    відображенням від’ємної частини симетрично осі Ох. Корені цієї параболи х₁ = 0 та х₂ = −3а , а  вершина знаходиться в точці і

Графіком є пряма, паралельна осі Ох.

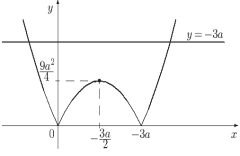
З малюнка слідує, що графіки даних функцій мають дві спільні точки при умові, що

Відповідь.

 

Приклад 26.  Вказати всі значення параметра a, при яких рівняння ((|x - 8| + |x - a|)²) - 7a(|x - 8| + |x - a|) + 10a² + 6a - 4 = 0

має лише два розв’язки.

Розв’язання

Замітимо, що маємо квадратне рівняння відносно t,

де t = |x − 8| + |x − a|. 

Перепишемо рівняння так, що застосувати теорему Вієта:

t² − 7at + 10a² + 6a - 4 = 0,
t² − 7at + 2(5a² + 3a - 2) = 0,
t² − 7at + 2(a + 1)(5a - 2) = 0,
t² − 7at + (2a + 2)(5a - 2) = 0.
Отже, корені цього рівняння:  (2a + 2) и (5a − 2).

Отримаємо: |x − 8| + |x − a| = 2a + 2 або

 |x − 8| + |x − a| = 5a − 2.

 Розглянемо  функцію  f(x) = |x − 8| + |x − a|.

Точки 8 і а ділять числову вісь на три області. Побудуємо відповідні графіки на кожному з цих проміжків.

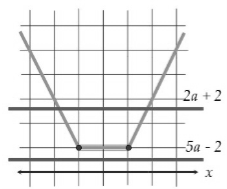
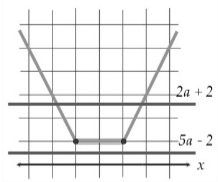
   При такому розташуванні прямі перетинатимуть графік лише у двох точках, при інших положеннях прямих, можливі й інші варіанти. Щоб знайти точки перетину, можна розв’язати дві системи строгих нерівностей або нерівність

( |x − 8| − (2a + 2))( |x − 8| − (5a − 2))< 0.

Скориставшись  методом інтервалів, отримуємо: a=    і

 a .

Відповідь.  a =    і  a .

Література

 

1. Мудрякова Н.Н. Урок–лекция «Уравнения и неравенства с параметром» [Электронный ресурс] // Режим доступа: http://festival.1september.ru/articles/531229/
2. Ромашко В. Д. Решение уравнений и неравенств с параметрами / В. Д. Ромашко [Электронный ресурс] // Режим доступа: http://parametry.narod.ru/reshenie2.html

3.      Фалилеева М.В. Методические аспекты обучения решению уравнений и неравенств с параметрами [Электронный ресурс] / М. В. Фалилеева // Фундаментальные исследования. – 2013. – № 4 (часть 5) – С. 1230-1235 Режим доступа: http://www.fundamental-research.ru/ru/article/view?id=31396

4. Прус А.В., Швець В.О. Задачі з параметрами в шкільному курсі математики. Навчально-методичний посібник. - Житомир: Вид-во «Рута», 2016. 468 с.