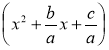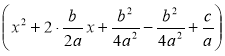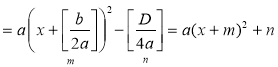Конспект уроку з алгебри 9 кл " квадратична функції її графік та властивості"

                                        Конспект уроку з алгебри 9 кл

Тема:  Квадратична функція, її графік і властивості

      Мета уроку: сформувати означення, вид графіка, його назву та алгоритм побудови графіка квадратичної функції, первинні вміння розпізнавати квадратичну функцію серед інших елементарних функцій, знаходити координати вершини та напрям гілок параболи , виконувати побудову графіка квадратичної функції за вивченим алгоритмом ,навчати аналізувати графік квадратичної функції, повторити загальні властивості функцій, розвивати логічне мислення, увагу, пам’ять;

 виховувати наполегливість, охайність, ціліспрямованість, повагу до іншої людини,вміння працювати в групі.

        Тип уроку: формування знань, вироблення первинних умінь.

Наочність та обладнання: ноутбук, проектор, презентація, картки з графіками квадратичної функції, «спідометр активності» ,опорний конспект, підручник, малюнки на дошці.

                                                            Хід уроку

І. Організаційний етап:

                     Підготовка приладдя.

                     Вправа : «Кулак,долоня,ребро»

 

II. Перевірка домашнього завдання:

                    В кого є питання по виконанню д.з.?(після уроку збираю зошити на перевірку).

                    Вправа « Закінчи речення»-питання в презентації,можна і роздрукувати та виконати в вигляді вправи «микрофон»:

1.Координатна площина складається з …

2.Вертикальна вісь називається…

3.Горизонтальна вісь називається…

4.Початок координат має координати …

5.Кожному значенню незалежної змінної ставиться у відповідність єдине значення залежної змінної-така залежність називається ….

6.Точка на площині має …

7.Функцію можна задати …способами.

8.Способи задання функції…

9.Незалежна змінна –це…

10.Залежна змінна-це...

11.Всі значення аргументу складають…

12. Всі значення ,що набуває функція ,складають …

13.Проміжки ,на яких функція набуває тільки додатні або тільки від’ємні значення називають проміжками…

14.При збільшенні значення аргументу збільшується значення функції,

то функція є…

15.При збільшенні значення аргументу зменшується значення функції,

то така функція називається…

16.Всі точки координатної площини,що мають координати,які відповідно дорівнюють :перша значенню аргумента

, а друга значенню функції називають…

 

III. Формулювання мети і завдань уроку.

Мета уроку:вивчити означення квадратичної функції, навчитися обчислювати вершину параболи,будувати графік квадратичної функції, аналізувати квадратичну  функцію за її графіком.

IV. Актуалізація опорних знань та вмінь учнів:

        1.Назвіть коефіцієнти квадратного тричлена:

    1) 5х² – 4х + 2;      2) 7х² – х;   3) -х² – 2х-3;   

     4) -х²;       5) 6х².

 

2. Опишіть перетворення, за допомогою якого з графіка y = f(x) можна побудувати графік функції g(x), якщо:

1) g(x) = -f(x);    2) g(x) = 2f(x);  

            3) g(x) = f(x + 2);        4) g(x) = f(x) – 2.

            3. Розв'яжіть рівняння:

               1) х² + х = 0;  2) х² + 2x + 1 = 0;

V. Формування знань

План вивчення нового матеріалу

1. Означення квадратичної функції.
2. Коефіцієнт при х²
3. Вершина параболи, вісь симетрії.
4. Розміщення графіка квадратичної функції на координатній площині.
5. Алгоритм побудови графіка функції y = ax² + bx + c.

Опорний конспект :

1.Функція виду у = ax² + bx + c, де а 0, називається квадра­тичною.

 2. Графік квадратичної функції — парабола, вітки якої на­прямлені вгору, якщо а > 0, і вниз — якщо а < 0 .

 Координати вершини (х₀; у₀) параболи графіка у = ах² + bх + с обчислюються за формулами:

 

3. Побудова графіка функції у = ах² + bх + с, а 0.

 

Спосіб 1	Спосіб 2
1. Обчислити абсцису вершини	1. Виділити повний квадрат: ах2 + bх + с = а=
2. Підставити х0 у рівняння і знайти у0. 3. Побудувати параболу у = ах2 з вершиною в точці (х0; у0). Якщо   а > 0, вітки парабо­ли напрямлені вгору, якщо а < 0 — вниз. 4. Для більшої точності побудови знайти точки перетину графіка з координатними осями.	= а= . 2. Використавши схему геоме­тричних перетворень графіків функцій, виконати побудову параболи          у = х2, потім її розтяг­нення (або стиснення) до параболи у = ах2, а потім виконати паралельне перенесення у = ах2 вздовж осі Ох на – т і вздовж осі Оу на п.

 

VI. Формування первинних умінь (робота з підручником)

Усні вправи:

 

 

 

 

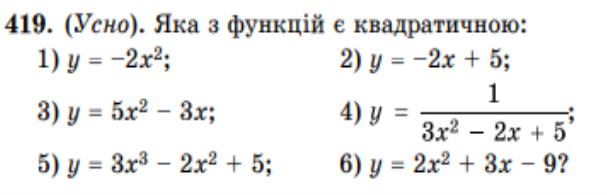
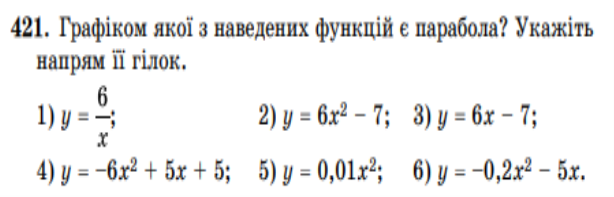
Письмові вправи:

Робота в графічному калькуляторі  :

https://www.geogebra.org/graphing?lang=ru

 

Усна вправа:

Проаналізувати графік квадратичної функції :

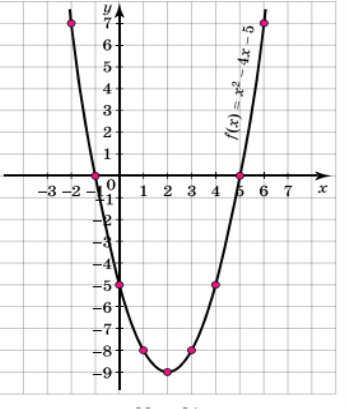
1.Область визначення функції

2.Область значеннь функції

3.Коєфіціент а.

4.Вершина параболи.

5.Вісь симетрії.

6.Нулі функції.

7.Проміжки знакосталості функції.

8.Проміжки зростання та спадання.

 

Робота в групах : Проаналізувати графік функції :

 

 

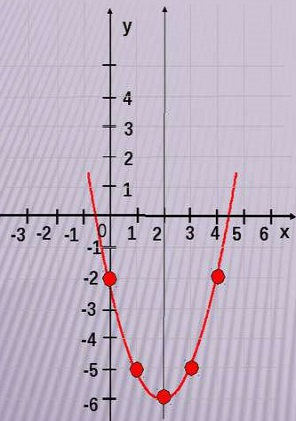
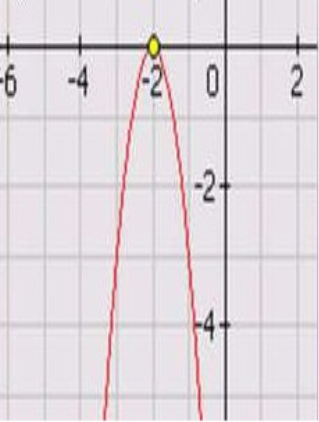
VII. Підсумки уроку

Що я дізнався нового?

Чого  нового я навчився?

Що було важко?

Позначте свої враження від уроку :

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

 

Заповните спідометр вашої активності на уроці:

 

                                       

    VIII.Домашнє завдання

1. Вивчити означення квадратичної функції, формулу для знаходження  вершини параболи алгоритм побудови графіка квадратичної функції,   §11 с.98-103
2. Розв'язати вправи різного рівня складності на застосування вивченого алгоритму. № 420,№423,№425,№431