Періодичність тригонометричних функцій. Графіки тригонометричних функцій та їх властивості
Тема: Періодичність тригонометричних функцій. Графіки тригонометричних функцій та їх властивості.
Мета: сформувати в учнів поняття «періодичність тригонометричних функцій», вміння будувати графіки тригонометричних функцій, знаходження найменших додатних періодів тригонометричних функцій, закріпити знання, здобуті на попередніх заняттях,; сформувати в учнів умінь знаходити періоди функцій у = sin (kx + b), у = cos (kx + b), у = tg (kx + b), у = ctg (kx + b).
Тип уроку: засвоєння нових знань
ХІД ЗАНЯТТЯ
- Організаційна частина.
- Перевірка домашнього завдання, перевірка раніше засвоєних знань
Проведення самостійної роботи.
І в. II в.
1. Побудуйте на одиничному колі точку Рα, на яку відображаються початкова точка Р0 (1; 0) при повороті на α рад навколо центра, якщо:
|
1. |
1. |
|
2. Знайдіть
|
2. Знайдіть
|
|
3. Визначте знак добутку sin 1 · cos 2 · tg 3. (5 балів) |
3. Визначте знак добутку сos 1 · sin 2 · ctg 3. (5 балів) |
Відповідь:
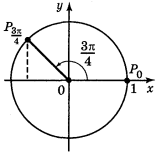
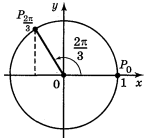
Рис. 2.11. Розв’язок до задачі 1(варіант1 і 2, відповідно)
І в.: 1. Рис. 55. 2. 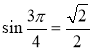 ,
, 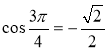 ,
, ![]() ,
, ![]() . 3. Плюс.
. 3. Плюс.
ІІ в.: 1. Рис. 56. 2. 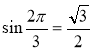 ,
, ![]() ,
, ![]() ,
, ![]() .3.Мінус.
.3.Мінус.
3. Мотивація навчальної роботи. Повідомлення теми і мети завдань.
Сьогодні на занятті ми з вами продовжимо розширювати наші знання про тригонометричні функції
4. Сприймання і первинне усвідомлення нового матеріалу, осмислення зв’язків і відношень в об’єктах вивчення.
1. Періодичність тригонометричних функцій доцільно демонструвати на рисунках (Рис. 2.12).
. 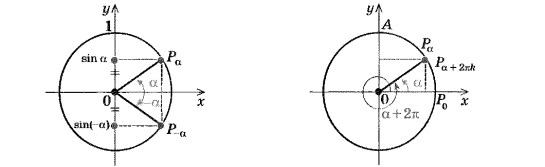
Рис. 2.12. Демонстрація періодичності функцій
2. Робота з презентаціями.
3. Робота з підручником (Істер О. С., ст.. 65–74).
Розглянемо, як розв’язані вправи в вашому підручнику.
4. Побудувати графік тригонометричних функцій.
Достатньо побудувати графік тригонометричної функції на відрізку, що дорівнює найменшому додатному періоду, який потім можна поширити на всю область визначення. Під час побудови графіка по точках використовуватимемо геометричну інтерпретацію кожної тригонометричної функції на одиничному колі.
Графік функції ![]() (Рис. 2.13) побудуємо на відрізку [0;2π]. Оскільки синус числа α – це ордината точки одиничного кола, в яку переходить точка Р0(1; 0) при повороті навколо центра на а рад, то побудуємо систему координат. Позначимо на осі Ox відрізок [0;2π], довжина якого наближено дорівнює
(Рис. 2.13) побудуємо на відрізку [0;2π]. Оскільки синус числа α – це ордината точки одиничного кола, в яку переходить точка Р0(1; 0) при повороті навколо центра на а рад, то побудуємо систему координат. Позначимо на осі Ox відрізок [0;2π], довжина якого наближено дорівнює ![]() .
.
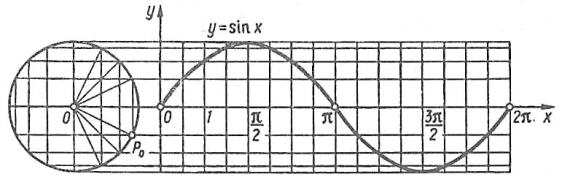
Рис. 2.13. Графік функції ![]()
Поза цим відрізком побудуємо коло з центром на осі Ox і радіусом, що дорівнює 1. Довжина кола також наближено дорівнює ![]() . Розіб’ємо відрізок [0;2π] і коло, починаючи від точки P0, на 16 рівних частин. Через кожну точку поділу проведемо прямі, паралельні осі Ox. 3 кожної точки поділу кола проведемо перпендикуляри до осі Ox, довжини яких дорівнюють ординаті, а отже, синусу кута, утвореного радіусом OP0 з віссю Ox і виміряного у радіанах. Кожна з цих ординат відповідає абсцисам α, позначеним точками поділу відрізка [0; 2π] на осі Ox. Провівши прямі, паралельні осі Oy в кожній точці поділу цього відрізка, до перетину з відповідною паралельною прямою, одержимо у перетині точки графіка функції
. Розіб’ємо відрізок [0;2π] і коло, починаючи від точки P0, на 16 рівних частин. Через кожну точку поділу проведемо прямі, паралельні осі Ox. 3 кожної точки поділу кола проведемо перпендикуляри до осі Ox, довжини яких дорівнюють ординаті, а отже, синусу кута, утвореного радіусом OP0 з віссю Ox і виміряного у радіанах. Кожна з цих ординат відповідає абсцисам α, позначеним точками поділу відрізка [0; 2π] на осі Ox. Провівши прямі, паралельні осі Oy в кожній точці поділу цього відрізка, до перетину з відповідною паралельною прямою, одержимо у перетині точки графіка функції ![]() . Проведена через ці точки суцільна крива називається синусоїдою.
. Проведена через ці точки суцільна крива називається синусоїдою.
Оскільки функція ![]() періодична з періодом 2nπ (Рис 2.14), де
періодична з періодом 2nπ (Рис 2.14), де ![]() , тобто
, тобто ![]() , то для продовження графіка за межі відрізка [0;2π] досить виконати побудову графіка функцій виду
, то для продовження графіка за межі відрізка [0;2π] досить виконати побудову графіка функцій виду ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , ... паралельно переносячи графік функції
, ... паралельно переносячи графік функції ![]() на 2π, 4π, 6π, ... одиниць ліворуч і праворуч.
на 2π, 4π, 6π, ... одиниць ліворуч і праворуч.

Рис. 2.14. Періодичність функції ![]()
Графік функції ![]() (Рис. 2.14) побудуємо, скориставшись формулою зведення
(Рис. 2.14) побудуємо, скориставшись формулою зведення ![]() і геометричним перетворенням відомого графіка. Отже,
і геометричним перетворенням відомого графіка. Отже, ![]() , тобто графік функції
, тобто графік функції ![]() можна одержати з графіка функції
можна одержати з графіка функції ![]() паралельним перенесенням його ліворуч уздовж осі Ox на
паралельним перенесенням його ліворуч уздовж осі Ox на ![]() одиниць.
одиниць.
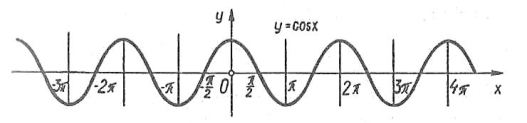
Рис. 2.15. Графік функції ![]()
Графік функції ![]() (Рис. 2.16) побудуємо за допомогою лінії тангенсів на проміжку
(Рис. 2.16) побудуємо за допомогою лінії тангенсів на проміжку ![]() довжина якого дорівнює періоду π цієї функції. Побудувавши систему координат і виділивши на осі Ox проміжок
довжина якого дорівнює періоду π цієї функції. Побудувавши систему координат і виділивши на осі Ox проміжок ![]() поза ним побудуємо одиничне коло з центром на осі Ox і лінію тангенсів. Поділимо проміжок
поза ним побудуємо одиничне коло з центром на осі Ox і лінію тангенсів. Поділимо проміжок ![]() і праве півколо на вісім рівних частин. Через центр кола і точки поділу його проведемо прямі до перетину з лінією тангенсів. Утворені точки перетину визначають відрізки на лінії тангенсів з довжиною, що дорівнює тангенсу відповідного кута повороту, виміряною в радіанах. Числові значення цих кутів, позначені на проміжку
і праве півколо на вісім рівних частин. Через центр кола і точки поділу його проведемо прямі до перетину з лінією тангенсів. Утворені точки перетину визначають відрізки на лінії тангенсів з довжиною, що дорівнює тангенсу відповідного кута повороту, виміряною в радіанах. Числові значення цих кутів, позначені на проміжку ![]() осі дорівнюють
осі дорівнюють ![]() .
.
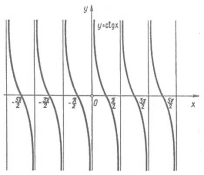

Рис. 2.16. Графіки функцій ![]() і
і ![]()
Через точки Tα на лінії тангенсів проведемо прямі, паралельні осі Ox, а через точки поділу проміжку ![]() паралельні осі Oy . Перетини цих паралельних прямих визначають точки, що належать графіку функції
паралельні осі Oy . Перетини цих паралельних прямих визначають точки, що належать графіку функції ![]() . Провівши плавну крину через ці точки, одержимо графік функції
. Провівши плавну крину через ці точки, одержимо графік функції ![]() на проміжку
на проміжку ![]() його межами, досить скористатися періодичністю функції тангенс, тобто тотожністю
його межами, досить скористатися періодичністю функції тангенс, тобто тотожністю ![]() . Отже, треба виконати побудову функцій виду
. Отже, треба виконати побудову функцій виду ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() , паралельним перенесенням графіка функції
, паралельним перенесенням графіка функції ![]() на π, 2π, 3π, ... одиниць ліворуч і праворуч. Графік функції
на π, 2π, 3π, ... одиниць ліворуч і праворуч. Графік функції ![]() називають тангенсоїдою.
називають тангенсоїдою.
Графік функції ![]() (Рис. 2.16) легко одержати, скориставшись формулою зведення
(Рис. 2.16) легко одержати, скориставшись формулою зведення ![]() ,
, ![]() і двома геометричними перетвореннями – паралельним перенесенням тангенсоїди на
і двома геометричними перетвореннями – паралельним перенесенням тангенсоїди на ![]() одиниць ліворуч і перетворенням симетрії утвореного графіка відносно осі Оx.
одиниць ліворуч і перетворенням симетрії утвореного графіка відносно осі Оx.
5. Узагальнення і систематизація знань.
1. Виконання вправ
с. 49 № 24 (1–5)
с. 49. № 27(1–2)
2. Доведіть твердження: якщо функція ![]() періодична з періодом Т, то функція
періодична з періодом Т, то функція ![]() також періодична з періодом
також періодична з періодом ![]() .
.
3. Побудувати графіки функцій ![]() ,
, ![]() (Рис. 2.17).
(Рис. 2.17).
Розв’язання. Використаємо геометричне перетворення відомого графіка функції ![]() . Якщо
. Якщо ![]() , то
, то ![]() . Відомо, що графік функції
. Відомо, що графік функції ![]() можна одержати з графіка функції
можна одержати з графіка функції ![]() стисненням його до осі Oy при k > 1 і розтягуванням від осі Oy при 0 < k < 1.
стисненням його до осі Oy при k > 1 і розтягуванням від осі Oy при 0 < k < 1.
Отже, графік функції ![]() можна одержати стисненням відомого графіка функції
можна одержати стисненням відомого графіка функції ![]() у два рази (Рис. 2.17.а), а графік функції
у два рази (Рис. 2.17.а), а графік функції ![]() – розтягуванням його у два рази (Рис. 2.17.б).
– розтягуванням його у два рази (Рис. 2.17.б).
4. Побудувати графік ![]() .
.
Розв’язання. Перетворимо вираз даної функції так, щоб перед аргументом у дужках залишився коефіцієнт, що дорівнює 1, тобто подамо у вигляді ![]() . Це дасть змогу пізніше використати побудову графіка функції
. Це дасть змогу пізніше використати побудову графіка функції ![]() , де а > 0, паралельним перенесенням у напрямі осі Ox уже відомого графіка функції.
, де а > 0, паралельним перенесенням у напрямі осі Ox уже відомого графіка функції.
Послідовність побудови шуканого графіка може бути такою:
-
будуємо відомий графік функції
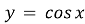 ;
;
-
будуємо графік функції
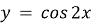 , стискаючи графік функції
, стискаючи графік функції 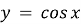 у два рази до осі Oy;
у два рази до осі Oy;
-
будуємо графік функції
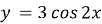 _y = 3cos2x, розтягуючи у три рази від осі Ox графік функції
_y = 3cos2x, розтягуючи у три рази від осі Ox графік функції 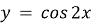 ;
;
-
будуємо шуканий графік
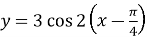 , паралельно переносячи раніше побудований графік
, паралельно переносячи раніше побудований графік 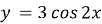 праворуч уздовж осі Ox на
праворуч уздовж осі Ox на  одиниць.
одиниць.
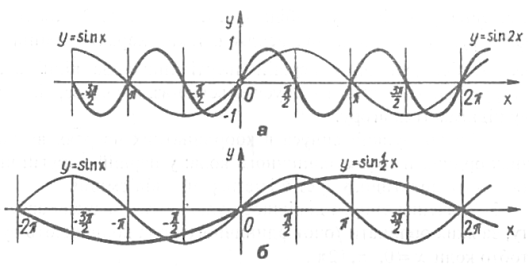
Рис. 2.17. Графік функції ![]()
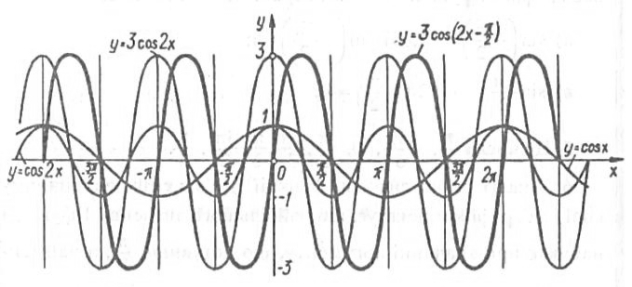
Рис. 2.17. Графік функції ![]()
6. Домашнє завдання.
7. Підсумки заняття.
Оцінювання роботи, підсумки. Вправа «Мікрофон»


про публікацію авторської розробки
Додати розробку
